9.2: Kepler's Second Law from Conservation of Angular Momentum

Last updated
Save as PDF

Page ID: 6842

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

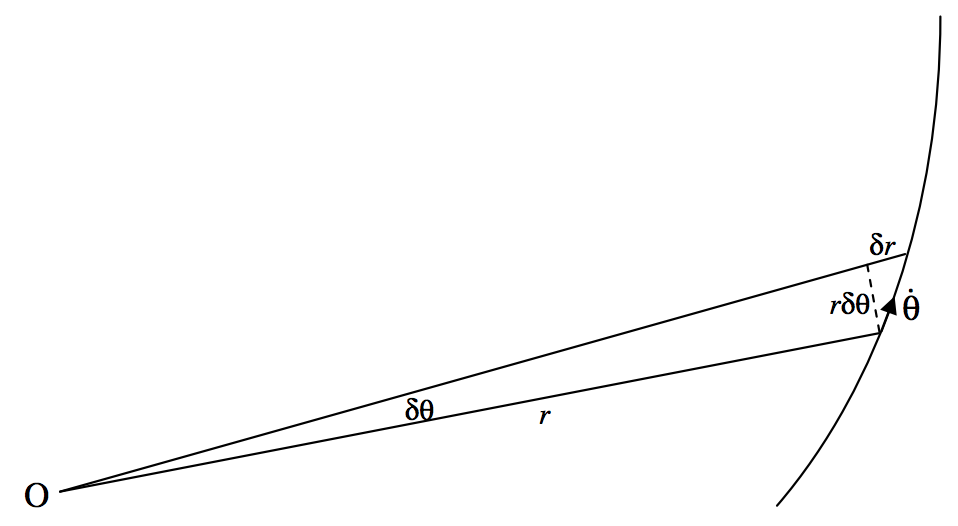
Figure 9.1.png
\(\text{FIGURE IX.1}\)

In figure \(\text{IX.1}\), a particle of mass \(m\) is moving in some sort of trajectory in which the only force on it is directed towards or away from the point \(\text{O}\). At some time, its polar coordinates are \((r, θ)\). At a time \(δt\) later these coordinates have increased by \(δr\) and \(δθ\).

Using the formula one half base times height for the area of a triangle, we see that the area swept out by the radius vector is approximately

\[δA = \frac{1}{2} r^2 δ θ+ \frac{1}{2} r δ θδ r. \label{9.3.1} \tag{9.3.1}\]

On dividing both sides by \(δt\) and taking the limit as \(δt → 0\), we see that the rate at which the radius vector sweeps out area is

\[\dot{A} = \frac{1}{2} r^2 \dot{θ}. \label{9.3.2} \tag{9.3.2}\]

But the angular momentum is , \(mr^2\dot{θ}\) and since this is constant, the areal speed is also constant. The areal speed, in fact, is half the angular momentum per unit mass.