11.3.3: Refraction
- Page ID
- 8207
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Refraction of starlight as it passes through Earth’s atmosphere displaces the position of the star towards the zenith. The amount of the refraction is not large close to the zenith, but it amounts to about half a degree near the horizon. Earth’s atmosphere is but a thin skin compared with the radius of Earth, and, provided that the star is not close to the horizon, we may treat the atmosphere as a plane-parallel atmosphere. The situation is illustrated in figure \(\text{XI.5}\).
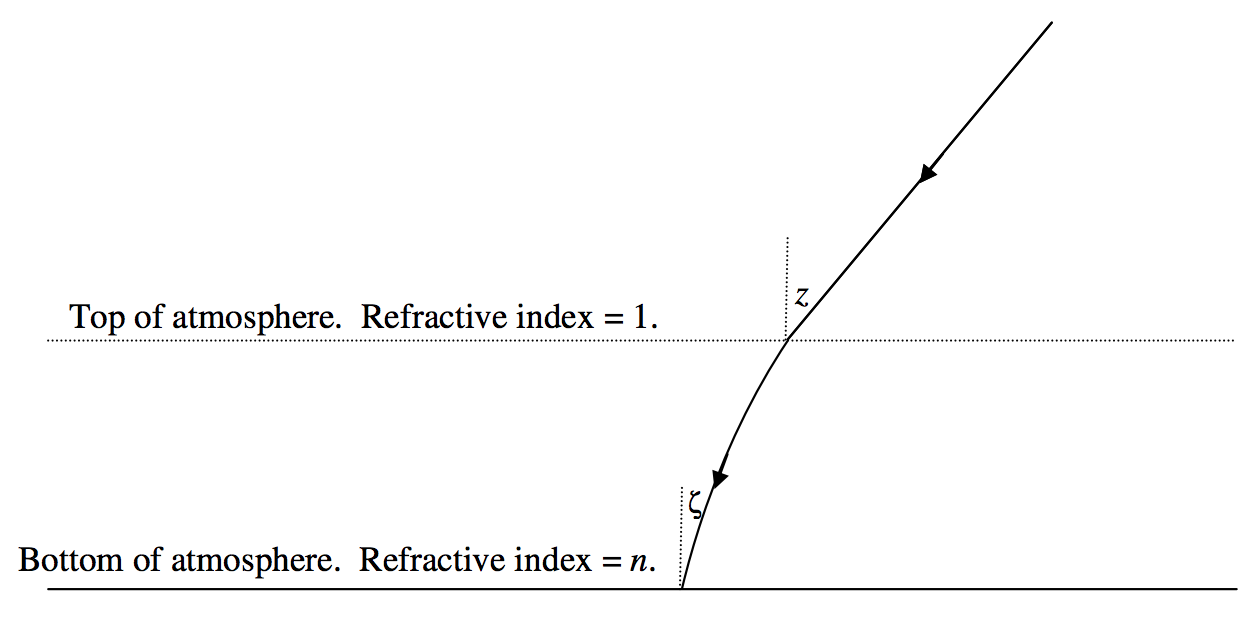
\(\text{FIGURE XI.5}\)
The angle \(z\) is the true zenith distance – i.e. the zenith distance it would have in the absence of an atmosphere. The angle \(ζ\) is the apparent zenith distance. By application of Snell’s law, we have \(\sin z = n\sin ζ\), and if we let \(ε = z − ζ\), this becomes
\[\sin ζ \cos ε + \cos ζ \sin ε = n \sin ζ . \label{11.3.1} \tag{11.3.1}\]
Divide both sides by \(\sin ζ\) and make the approximations (correct to first order in \(ε\)) \(\sin ε ≈ ε\), \(\cos ε ≈ 1\), and we obtain
\[ε = z - ζ = (n-1) \tan ζ . \label{11.3.2} \tag{11.3.2}\]
The refractive index at ground level varies a little with temperature and pressure, but it averages about \(n − 1 = 58^".2\). (You didn’t know that refractive index was expressed in arcseconds, did you?)
We have made some approximations in deriving Equation \ref{11.3.2}, but it must be borne in mind that, as far as astrometry is concerned, what is important is the differential refraction between the bottom and top of the detector (photographic film or \(\text{CCD}\)), and Equation \ref{11.3.2} should be more than adequate – unless one is observing very close to the horizon. The only time when one is likely to be observing close to the horizon would be for a bright comet, for which it is very difficult to make precise measurements anyway. The differential refraction between top and bottom obviously amounts to
\[δε = (n-1) \sec^2 ζ δζ , \label{11.3.3} \tag{11.3.3}\]
where \(δζ\) is the range of zenith distance covered by the detector. In the table below I show the differential refraction between top and bottom of a detector (such as a photographic film) with a 5-degree field, and for a detector (such as a \(\text{CCD}\)) with a 20- arcminute field, for four zenith distances. Obviously, the correction for differential refraction should be made for the 5-degree photographic field. It might be argued that, for the relatively small field of a 20-arcminute \(\text{CCD}\), the correction for differential refraction is unimportant. However, the precision expected for modern \(\text{CCD}\) astrometry is rather higher than the precision that was expected during the photographic era, and certainly, for large zenith distances, if one hopes for sub-arcsecond astrometry, a correction for differential refraction is desirable. Bear in mind, too, that CCDs are becoming larger as technology advances, and that the larger the CCD, the more important will be the refraction correction.
\begin{array}{c c c}
\text{Zenith distance} & δε \ \text{in arcseconds} & δε \ \text{in arcseconds} \\
\text{in degrees} & \text{for } 5^\circ \text{ field} & \text{for } 20^\prime \text{ field} \\
\\
15 & 5.5 & 0.4 \\
30 & 6.8 & 0.5 \\
45 & 10.2 & 0.7 \\
60 & 20.4 & 1.4 \\
\end{array}
The most straightforward way of correcting for differential refraction is to calculate the true zenith distance \(z\) and azimuth \(A\) of each comparison star by the usual methods of spherical astronomy:
\[\cos z = \sin \phi \sin δ + \cos \phi \cos δ \cos H \label{11.3.4} \tag{11.3.4}\]
and \[ \tan A = \frac{\sin H}{\cos \phi \tanδ - \sin \phi \cos H}. \label{11.3.5} \tag{11.3.5}\]
Here \(\phi\) is the observer’s latitude, and \(H\) is the hour angle of the star, to be found from its right ascension and the local sidereal time. Having found \(z\), then calculate the apparent zenith distance \(ζ\) from Equation \ref{11.3.2} (refraction does not, of course, change the azimuth), and then invert Equations \ref{11.3.4} and \ref{11.3.5} to obtain the apparent hour angle \(H^\prime\) (and hence apparent right ascension \(α^\prime\)) and apparent declination \(δ^\prime\) of the star. Do this for all the comparison stars. (By hand, this might sound long and tedious, but of course when a computer is programmed to do it, it is all automatic and instantaneous.)
\[\sin δ^\prime = \sin \phi \cos ζ + \cos \phi \sin ζ \cos A \label{11.3.6} \tag{11.3.6}\]
and \[\tan H^\prime = \frac{\sin A \tan ζ}{\cos \phi - \sin \phi \cos A \tan ζ}. \label{11.3.7} \tag{11.3.7}\]
You can then carry out the measurements and from them calculate the apparent right ascension and declination of the asteroid. From these, calculate the apparent zenith distance. Correct this to obtain the true zenith distance, and finally calculate the true right ascension and declination of the asteroid – again all of this is done instantaneously once you have correctly programmed the computer.
Another aspect of refraction that might be considered is that blue (early-type) stars are refracted more than red (late-type) stars. In principle, therefore, one should use only comparison stars that are of the same colour as the asteroid. In practice, I imagine that few astrometrists always do this. If, by ill-fortune, one of the comparison stars is very red or very blue, this may result in a large residual for that star, and the star can be detected and rejected, as described in subsection \ref{11.3.6}. Yet another aspect is that, because of dispersion, the light from the star – especially if it is low down near the horizon − will be drawn out into a short spectrum, with the red end closer to the horizon than the blue end, and there is then a problem of how to measure the position of the star. The answer is probably to leave asteroids that are close to the horizon to observers who are at a more favourable latitude. As mentioned above, the only time you are likely to observe very low down would be for a long-period comet, on which you cannot set extremely precisely in any case.


