18.7: Measuring the Radial Velocity
( \newcommand{\kernel}{\mathrm{null}\,}\)
In a text primarily concerned with celestial mechanics, I shan’t attempt to do justice to the practical details of measuring a spectrum, but one or two points are worth mentioning, if only to draw the reader’s attention to them.
To measure the radial velocity, you obtain a spectrum of the star and you measure the wavelength of a number of spectrum lines (i.e. your measure their positions along the length of the spectrum) and you compare the wavelengths with the wavelengths of a comparison laboratory spectrum, such as an arc or a discharge tube, adjacent to the stellar spectrum. If the spectra are obtained on a photographic plate, the measurement is done with a measuring microscope. If they are obtained on a CCD, there is really no “measurement” in the traditional sense to be done – a computer will read the pixels on which the lines fall. If the stellar lines are displaced by Δλ from their laboratory values λ, then the radial velocity v is given simply by
vc=Δλλ.
Note that this formula, in which c is the speed of light, is valid only if v << c. This is certainly the case in the present context, though it is not correct for measuring the radial velocities of distant galaxies. (The z in the galaxy context is the measured Δλ/λ, and knowledge of both relativity and cosmology is necessary to translate that correctly into radial velocity.)
The accurate measurement of wavelengths in stellar spectra has its own set of difficulties. For example, the spectrum lines of early type stars are broad and diffuse as a result of the high temperatures and quadratic Stark broadening of the lines, as well as the rapid rotation of early type stars. The lines of late-type stars are numerous, closely crowded together and blended. Thus there are difficulties at both ends of the spectral sequence.
One very nice technique for measuring radial velocities involves making use of the entire spectrum rather than the laborious process of measuring the wavelengths of individual lines. Suppose that you are, for example observing a G-type star. You will prepare an opaque mask on which are inscribed, in their correct positions, transparent lines corresponding to the lines expected of a G-type star. During observation, the spectrum of the star is allowed to fall on this mask. Some light gets through the transparent inscribed lines on the mask, and this light is detected by a photoelectric cell behind the mask. The mask is moved parallel to the spectrum until the dark absorption lines in the stellar spectrum fall on the transparent inscribed lines on the mask, and at this moment the amount of light passing through the mask and reaching the photoelectric cell reaches a sharp minimum. Not only does this technique make use of the whole spectrum, but the radial velocity is obtained immediately, in situ, at the telescope.
I end by briefly mentioning two little problems that are well known to observers, known as the rotation effect and the blending effect.
If the orbital inclination is close to 90o, the system, as well as being a spectroscopic binary, might also be an eclipsing binary. In this case, we can in principle get a great deal of information about the system – but there is a danger that the information might not be correct. For example, suppose that the system is a single-lined binary, and that the bright star (the one whose spectrum can be seen) is a rapid rotator and is being partially eclipsed by the secondary. In that case we can see only part of the surface of the primary star – perhaps that part of the star that is (by rotation) moving towards us. This will give us a wrong measurement of the radial velocity.
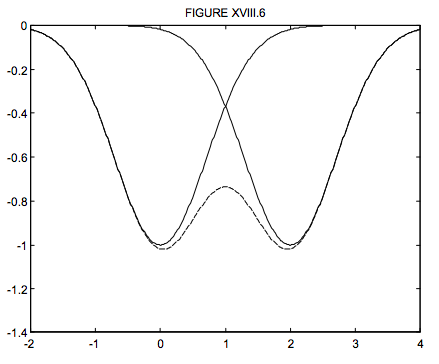
Or again, suppose that we have a double-lined binary. For much of the orbital period, the lines from one star may be well separated from those of the other. However, there comes a time when the two sets of lines approach each other and become partially blended. I show in figure XVIII.6 two partially blended gaussian profiles. You will see that the minima of the blended profile, shown as a dashed curve, occur closer together than the true minima of the individual lines. If you measure the minima of the blended profile, this will obviously give the wrong radial velocity and will result in a distortion of the velocity curve and corresponding errors in the orbital elements. Many years ago I made some calculations on the amount of the blending effect for gaussian and lorentzian profiles for various separations and relative intensities. These calculations were published in Monthly Notices of the Royal Astronomical Society, 141, 43 (1968).