5.7: A Series of Problems

I am now going to embark upon a series of problems that at first sight may appear to be not very relevant to stellar atmospheres, but the reader is urged to be patient and look at them, partly because they make use of many of the ideas encountered up to this point, and also because they culminate in determining how the flux and the mean specific intensity in an atmosphere increase with optical depth in terms of the source function.

Problem 1

An infinite plane radiating surface has a uniform specific intensity (radiance) \(I\). What is the flux (irradiance) at a point \(\text{P}\), situated at a height \(h\) above the surface?

We have already answered that question in equation 1.15.3, and the answer, which, unsurprisingly since the plane is infinite in extent, is independent of \(h\), is \(\pi I\), so let's get on with

Problem 2

Same as Problem 1, except that this time the space between the radiating plane and the point \(\text{P}\) is filled with a uniform gas of absorption coefficient \(\alpha\). The specific intensity (radiance) of the surface, we are told, is, following astrophysical custom, \(I\). Unfortunately I shall also be compelled to make use of "intensity" in the "standard" sense of Chapter 1, and for that I shall use the symbol \(\Im\).

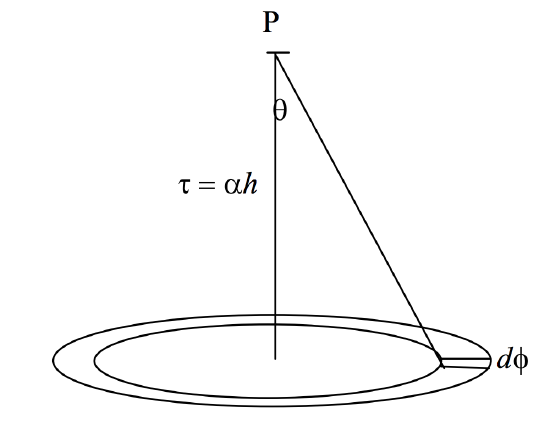
\(\text{FIGURE V.2}\)

The elemental area is \(r \ dr \ d\phi\), or, since \(r = h \tan \theta\), it is \(h^2 \tan \theta \sec^2 \theta d\theta d\phi\). The intensity of the elemental area towards \(\text{P}\) is the specific intensity (radiance) times the projected area:

\[d\Im = Ih^2\tan \theta \sec^2 \theta \ d\phi \ \cos\theta\]

If there were no absorption, the irradiance of \(\text{P}\) by the elemental area would be

\[d\Im \cos \theta / (h^2 \sec^2 \theta),\]

which becomes \[I \sin \theta \cos \theta \ d \theta \ d \phi .\]

But it is reduced by absorption by a factor \(e^{−\tau \sec \theta}\), where \(\tau = \alpha h\). Therefore the irradiance of \(\text{P}\) by the elemental area is

\[Ie^{-\tau \sec \theta} \sin \theta \cos \theta \ d\theta \ d \phi .\]

For the irradiance at \(\text{P}\) (or "flux" in the astrophysics sense) by the entire infinite plane we integrate from \(\phi = 0\) to \(2\pi\) and \(\theta = 0\) to \(\pi/2\), to obtain

\[2\pi I \int_0^{\pi/2} e^{-\tau \sec \theta} \sin \theta \cos \theta d\theta\]

If we now write \(x = \sec \theta\), this becomes

\[\text{Irradiance at P} = 2\pi I E_3 (\tau),\]

and we hope that the reader has not forgotten the meaning of \(E_3\) - if you have, as the game of snakes and ladders would say, Go back to Chapter 3. Note that, at \(\tau = 0\), this becomes \(\pi I\), as expected.

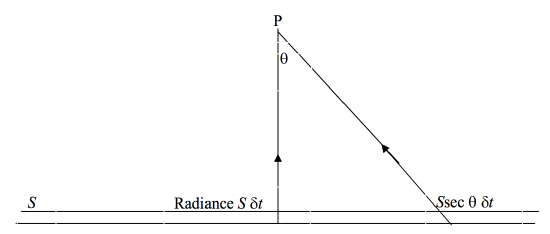
\(\text{FIGURE V.3}\)

A point \(\text{P}\) is situated at a height \(h\) above an infinite plane slice of gas of optical thickness \(\delta \tau\) and source function \(S\). There is nothing between \(\text{P}\) and the slice of gas. What is the flux (irradiance) at \(\text{P}\)?

At first glance this appears to be identical to Problem 1, except that the specific intensity of the slice is \(S\delta t\). However, a more careful look at the diagram will reveal that the specific intensity of the slice is by no means uniform. It is darkest directly below \(\text{P}\), and, when \(\text{P}\) looks farther from his nadir, the slice gets brighter and brighter, being \(S \ \sec \theta \ \delta t\) at an angle \(\theta\). The upwards flux ("irradiance") at \(\text{P}\) is therefore

\[F_+ = 2 \pi S \delta t \int_0^{\pi/2} \sec \theta \cos \theta \sin \theta \ d\theta = 2\pi S \delta t\]

Same as Problem 3, except that this time we'll place an absorbing gas of optical thickness \(t\) between \(\text{P}\) and the slice \(\delta t\).

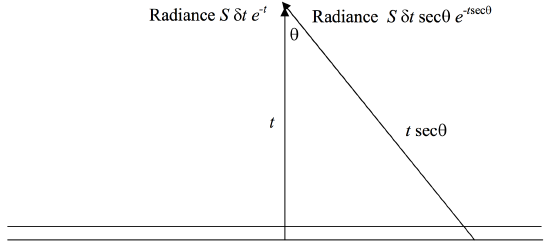
\(\text{FIGURE V.4}\)

In that case the flux (irradiance) at \(\text{P}\) from an element at an angle \(\theta\) is reduced by \(e^{-t \sec \theta}\) and consequently the flux at \(\text{P}\) from the entire slice is

\[F_+ = 2\pi S \delta t \int_0^{\pi/2} \sec \theta \cos \theta \sin \theta \ d\theta = 2\pi S \delta t .\]

If we write \(x = \sec \theta\), we very soon see that this is

\[\text{Flux (irradiance) at P} = 2\pi S \delta t E_2 (t)\]

Problem 5 (an important result in atmosphere theory)

Now consider a point \(\text{P}\) at an optical depth \(\tau\) in a stellar atmosphere. (The use of the word "depth" will imply that \(\tau\) is measured downwards from the surface towards the centre of the star.) We shall assume a plane parallel atmosphere i.e. a shallow atmosphere, or one than is shallow compared with the radius of the star, or we are not going to go very deep into the atmosphere. The point \(\text{P}\) is embedded in an absorbing, scattering, emitting gas. The flux coming up from below is equal to contributions from all the slices beneath \(\text{P}\), from \(t = \tau\) to \(t = \infty\):

\[F_+ = 2\pi \int_\tau^\infty S(t) E_2 (t-\tau) dt \]

The flux pouring down from above is the contribution from all the slices above, from \(t = 0\) to \(t = \tau\) :

\[F_- = 2\pi \int_0^\tau S(t) E_2 (\tau - t) dt\]

The net upward flux at a point \(\text{P}\) at an optical depth \(\tau\) in an absorbing, scattering, emitting atmosphere is

\[F(\tau) = 2\pi \left[ \int_\tau^\infty S(t) E_2 (t-\tau) dt - \int_0^\tau S(t) E_2 (\tau-t)dt \right] \label{5.7.1} \tag{5.7.1}\]

The integral \(H\) is just \(1/(4\pi)\) times this.

The reader is now asked to find the integrals \(J(\tau)\) and \(K\tau)\). These should be given in the form of integrals that include a source function \(S(t)\) and an exponential integral function \(E(t − \tau)\) or \(E(\tau − t)\). It is important to get the argument the right way round. One way is right; the other is wrong.

Problem 6

This is an easier problem, though the result is nevertheless important.

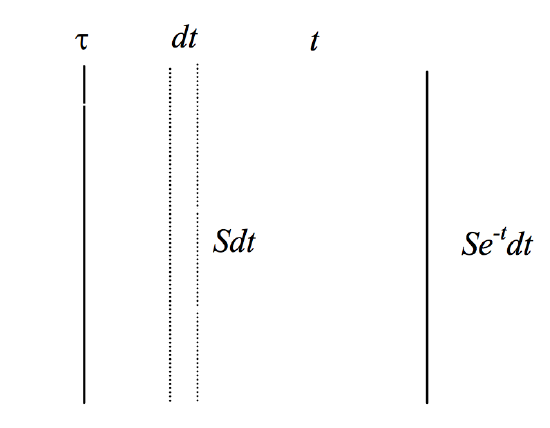
\(\text{FIGURE V.5}\)

Figure V.5 shows a slab of gas of optical thickness \(\tau\). The observer is supposed to be to the right of the slab, and optical depth is measured from the right hand face of the slab towards the left. At an optical depth \(t\) within the slab is a slice of optical thickness \(dt\). The slab is supposed to have a uniform source function \(S\) throughout. Source function is specific intensity per unit optical thickness, so the specific intensity of the slice is \(Sdt\). The emergent intensity from this slice, by the time that it reaches the right hand surface of the slab, is \(Se^{-t} dt\). The emergent specific intensity of the entire slab is the sum of the contributions of all such slices throughout the slab; that is \(\int_0^\tau Se^{-t}dt\). If the source function is uniform throughout the slab, so that \(S\) is not a function of \(t\), we find that the emergent specific intensity of the slab is

\[I = S \left( 1-e^{-t} \right) \label{5.7.2} \tag{5.7.2}\]

Problem. A quantity of hot gas is held in a box 50 cm long. The emission coefficient of the gas is \(0.06 \ \text{W sr}^{−1} \text {m}^{−3}\) and the extinction coefficient is \(0.025 \ \text{cm}^{−1}\). What is the emergent specific intensity (radiance)? (I make it \(1.71 \times 10^{−2} \text{W m}^{−2} \text{sr}^{−1}\).)