9.1: Introduction, Radiance, and Equivalent Width
( \newcommand{\kernel}{\mathrm{null}\,}\)
If we look at a hot, glowing gas, we can imagine that we could measure its radiance in W m−2 sr−1. If we disperse the light with a spectrograph, we may see that it is made up of numerous discrete emission lines. These lines are not infinitesimally narrow, but have a finite width and a measurable profile. At any particular wavelength within the wavelength interval covered by the line, let us suppose that the radiance per unit wavelength interval is Iλ W m−2 sr−1 m−1. Here, we are using the symbol I for radiance, which is customary in astronomy, rather than the symbol L, which we used in chapter 1. We insist, however, on the correct use of the word "radiance", rather than the often too-loosely used "intensity". We might imagine that we could measure Iλ by comparing the radiance per unit wavelength interval in the spectrum of the gas with the radiance per unit wavelength interval of a black body at a known temperature (or of any other body whose emissivity is known), observed under the same conditions with the same spectrograph.
The radiance I of the whole line is given by I=∫∞0Iλdλ. In principle, the integration limits are 0 and ∞, although in practice for most lines the integration need be performed only within a few tenths of a nanometer from the line center.
The radiance of an emission line depends, among other things, upon the number of atoms per unit area in the line of sight (the "column density") in the initial (i.e. upper) level of the line.
You will have noticed that I wrote "depends upon", rather than "is proportional to". We may imagine that the number of atoms per unit area in the line of sight could be doubled either by doubling the density (number of atoms per unit volume), or by doubling the depth of the layer of gas. If doubling the column density results in a doubling of the radiance of the line, or, expressed otherwise, if the radiance of a line is linearly proportional to the column density, the line is said to be optically thin. Very often a line is not optically thin, and the radiance is not proportional to the number of atoms per unit area in the upper level. We shall return to this topic in the chapter on the curve of growth. In the meantime, in this chapter, unless stated otherwise, we shall be concerned entirely with optically thin sources, in which case I∝N2, where N is the column density and the subscript denotes the upper level. We shall also suppose that the gas is homogenous and of a single, uniform temperature and pressure throughout.
In the matter of notation, I am using:
n=number of atoms per unit volumeN=column densityN=number of atoms
Thus in a volume V,N=nV, and in a layer of thickness t,N=nt.
Most lines in stellar spectra are absorption lines seen against a brighter continuum. In an analogous laboratory situation, we may imagine a uniform layer of gas seen against a continuum. We'll suppose that the radiance per unit wavelength interval of the background continuum source is Iλ(c). We shall establish further notation by referring to figure IX.1, which represents an absorption line against a continuum. The radiance per unit wavelength interval is plotted against wavelength horizontally.
FIGURE IX.1
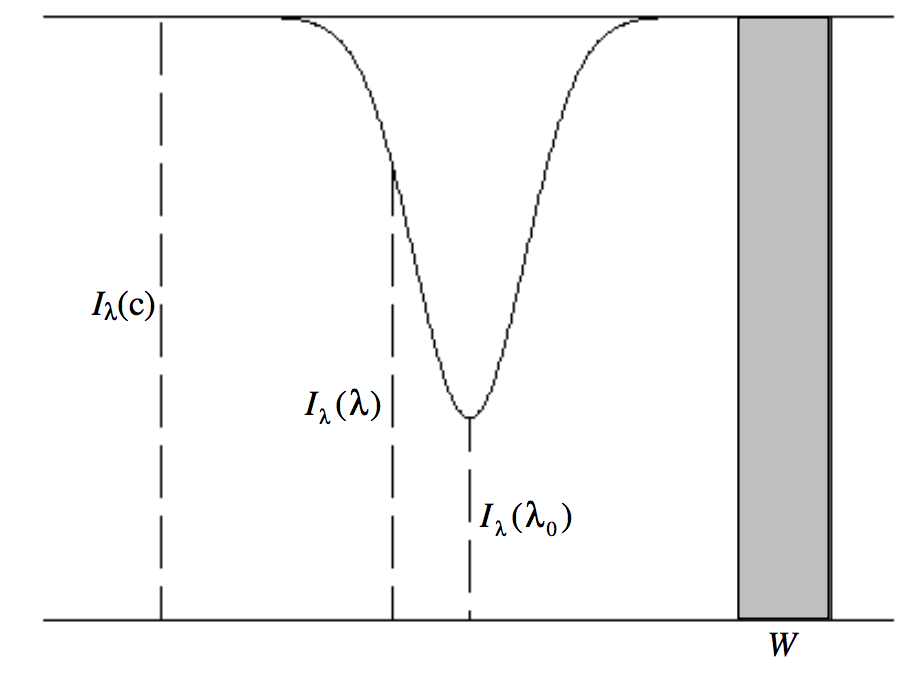
Iλ(λ) is the radiance per unit wavelength interval at some wavelength within the line profile, and Iλ(λ0) is the radiance per unit wavelength interval at the line center.
The equivalent width W (dieAequivalentbreite) of an absorption line is the width of the adjacent continuum that has the same area as is taken up by the absorption line. Expressed as a defining equation, this means:
WIλ(c)=∫[Iλ(c)−Iλ(λ)]dλ.
Again in principle the integration limits are 0 to ∞, although in practice a few tenths of a nanometre will suffice. Equivalent width is expressed in nm (or in Å). It must be stressed that equivalent width is a measure of the strength of an absorption line, and is in no way related to the actual width (or full width at half minimum) of the line. In figure IX.1, the width W of the continuum has the same area as the absorption line.
In principle, the equivalent width could also be expressed in frequency units (Hz), via a defining equation:
W(ν)Iν(c)=∫[Iν(c)−Iν(ν)]dν.
This is sometimes seen in theoretical discussions, but in practice equivalent width is usually expressed in wavelength units. The two are related by
W(ν)=cλ2W(λ),W(λ)=cν2W(ν).
Unless otherwise specified, I shall omit the superscript (λ), and W will normally mean equivalent width expressed in wavelength units, as in Equation ???.
A layer of cool gas lies above an extended source of continuous radiation, and an absorption line formed in the gas layer has an equivalent width W. If the temperature of the extended continuous source is now increased so that its spectral radiance at the wavelength of the line is doubled, what will now be the equivalent width of the line?
The equivalent width of an absorption line depends, among other things, upon the number of atoms per unit area in the line of sight (the "column density") in the initial (i.e. lower) level of the line. If the gas is optically thin, W∝N1, where the subscript indicates the lower level of the line.
If the absorption coefficient at wavelength λ is α(λ) and has the same value throughout the gas, and it the thickness of the gas layer is t,Iλ(λ) and Iλ(c) are related by
Iλ(λ)=Iλ(c)exp[−α(λ)t].
Thus Equation ??? can be written
W=∫[1−exp(−α(λ)t)]dλ,
and this equation is sometimes cited as the definition of the equivalent width. The definition, however, is Equation ???. Equation ??? can be used to calculate it, but only if α(λ) is uniform throughout the gas. In the optically thin limit, the first term in the Maclaurin expansion of 1−exp(−α(λ)t) is α(λ)t, so that, for an optically thin homogeneous gas,
W=t∫α(λ)dλ.
The reader should verify, as ever, the dimensional correctness of all of the foregoing equations.
We have seen that the radiance of an emission line or the equivalent width of an absorption line depends, among other things, on the column density of atoms in the initial state. In fact, in a homogeneous optically thin gas, the radiance or equivalent width is linearly proportional to the product of two things. One is the column density of atoms in the initial state. The other is an intrinsic property of the atom, or rather of the two atomic levels involved in the formation of the line, which determines how much energy a single atom emits or absorbs. There are three quantities commonly used to describe this property, namely oscillator strength, Einstein coefficient and line strength.
All three of these quantities are related by simple equations, but oscillator strength is particularly appropriate when discussing absorption lines, Einstein coefficient is particularly appropriate when discussing emission lines, while line strength is a quantum mechanical quantity particularly useful in theoretical work. Because of this very technical usage of the term line strength, the term should not be used merely to describe how "intense" a particular line appears to be.


