10.5: Pressure Broadening

This is a fairly difficult subject, and I am no expert in it. The reader will forgive me if I accordingly treat it rather briefly and descriptively.

The phenomena of pressure broadening (also known as collisional broadening) are often divided into effects resulting from the short time interval between atomic collisions, and effects resulting at the moment of collision. I shall begin by describing the first of these phenomena.

The only possible absolutely monochromatic unbroadened infinitesimally narrow line with a single, uniquely defined frequency is a sine wave of infinite extent. A sine wave of finite length is not a true sine wave of a single frequency, but it has a spread of component frequencies, which can be determined by Fourier analysis. This, by the way, is the reason behind Heisenberg’s uncertainty principle (Unsicherheitsprinzip). If the wavefunction that describes a particle is very limited in extent, then the position of the particle is relatively well determined. On the other hand, the limited extent of the wavefunction means that it has a correspondingly broad Fourier spread of constituent wavelengths, and hence the momentum is correspondingly uncertain.

The atmospheres of giant and supergiant stars are relatively thin; pressure broadening is slight and lines tend to be narrow. In the atmospheres of main sequence stars, however, collisions between atoms are frequent. The frequent occurrence of collisions interrupts the wave trains and divides them into short wave-packets, with a corresponding spread of component frequencies. Thus the spectrum lines are broadened.

The Fourier distribution of amplitudes of component frequencies of a sine wave that is truncated by a box function is the same as the Fourier distribution of amplitudes of a light wave that is diffracted by a single slit. That is to say it is a sinc function of the form \((\sin \Delta ν)/ \Delta ν\) and the intensity distribution is the square of this. The shorter the intercollision time, the wider the spread of constituent frequencies, just as a narrow slit produces a wide diffraction pattern. Thus one might expect the profile of a pressure broadened line to resemble a single slit diffraction pattern, which, it will be recalled, looks like figure X.5.

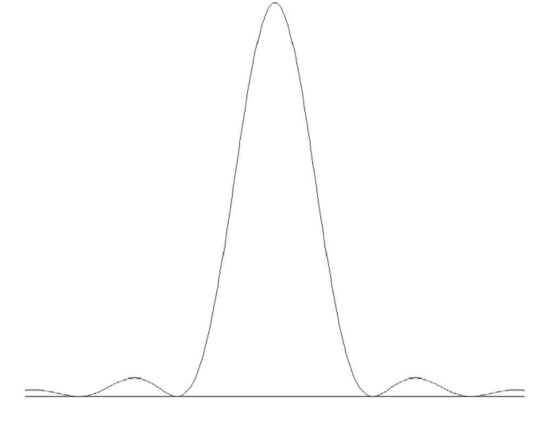
\(\text{FIGURE X.5}\)

The profile would indeed look like that if all intercollision times were exactly equal and all wave-train fragments were of exactly the same length. There is, however, a Poisson distribution of intercollision times, and so the above profile has to be convolved with this Poisson distribution. While I don’t do the calculation here, the resulting profile is a Lorentz profile except that the damping constant \(\Gamma\) is replaced by \(2 / \overline t\), where \(\overline t\) is the mean time between collisions. The mean time between collisions is given, from kinetic theory of gases, by

\[\label{10.6.1}\overline t =\frac{1}{nd^2}\sqrt{\frac{m}{16\pi kT}}.\]

Here \(m,\, d\text{ and }n\) are, respectively, the masses, diameters and number density of the atoms. Hence, if the kinetic temperature is independently known, the number density of the particles can be determined from the FWHm of a pressure-broadened line.

It will be recalled that classical radiation damping theory predicts the same FWHm for all lines, with a classical damping constant \(\gamma\). Quantum mechanical theory predicts a damping constant \(\Gamma\) and hence FWHm that differs from line to line. Yet in the spectrum of a main sequence star, one quite often finds that all lines of a given element have the same FWHm and hence the same effective damping constant. This is because the width of a Lorentz profile is determined more by pressure broadening than by radiation damping.

There are further broadening effects caused by interactions that take place at the moment of collision. If an atom is approached by an electron or an ion, it will temporarily be in an electric field, and consequently the lines will be broadened by Stark effect, which may be either linear (proportional to the electric field \(E\)) or quadratic (\(\propto E^2\)), or neutral-neutral reactions give rise to interactions between temporarily induced dipole moments (van der Waals forces), and these all have different dependences on interatomic distance. Neutral magnesium is very sensitive to quadratic Stark effect, and hydrogen is sensitive to linear Stark effect. The entire subject is quite difficult, and I leave it here except to point out two small details. Very often the broadening is not symmetric, lines typically having wider wings to the long wavelength side than on the short wavelength side. This is because the effect of the interactions is to lower and broaden the energy levels of a transition, the lower energy level generally being lowered more than the upper. A second point is that the hydrogen Balmer lines are often much broadened by linear Stark effect, and this can be recognized because the Stark pattern for the Balmer series is such that there are no undisplaced Stark components for even members of the series – \(\text{H}\beta,\, \text{H}\delta,\, \text{H}ζ,\) etc. Thus results in a central dip to these lines in an emission spectrum or a central bump in an absorption line.