3: Heliocentric Parallax

The simplest way to measure the distance to an object via parallax is to make simultaneous measurements from two locations on Earth. However, as we saw last time, this method only works for objects which are relatively nearby:

Table 1

Object	maximum possible parallax (arcseconds)
Mars	34
Jupiter	4
Neptune	0.6
Proxima Centauri	0.00007

In short, simultaneous two-location measurements will only work for bodies within our own solar system. We need to find some larger baseline to measure the parallax to other stars....

A longer baseline: the orbit of the Earth around the Sun

Astronomers need a VERY long baseline in order to produce a parallax angle which is large enough to detect via conventional imaging. Fortunately, there is a convenient baseline just waiting to be used -- if we are willing to discard the requirement that measurements be simultaneous (more on this later). This longer baseline is the radius of the Earth's orbit around the Sun:

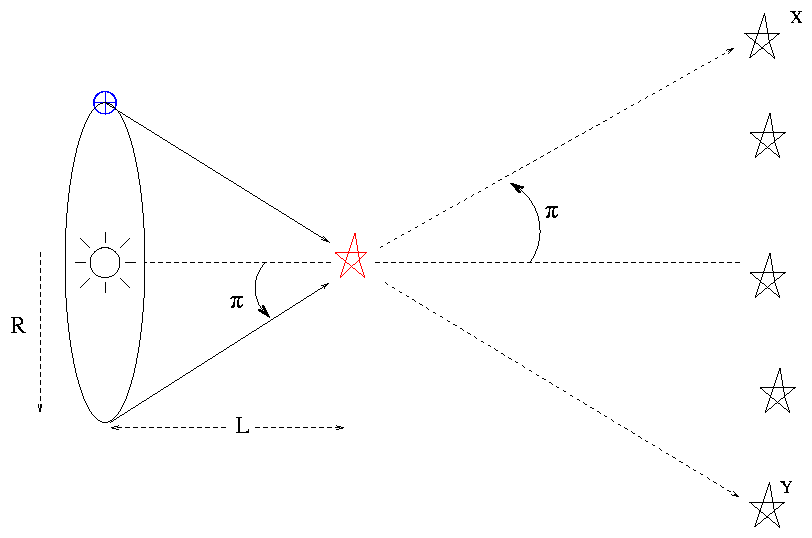
Note the convention used only in this situation: the quoted "heliocentric parallax angle" π (pi) is always HALF the apparent angular shift.

So, if we measure a parallax half-angle π (pi) to a star, we can calculate its distance very simply:

\[L = \frac{R}{\tan(\pi)}\]

where

\[R = 149.6 \times 10^{6} km \; = \; 1 \; \mathsf{Astronomical} \; \mathsf{Unit} \; (AU)\]

Small angles and peculiar units make life easy

Now, for small angles -- and the angles are always small for stars -- we can use the small angle approximations:

\[\tan(\pi) \quad \approx \quad \sin(\pi) \quad \approx \quad \pi\]

as long as we measure the angle in radians. Even if we don't use radians, it still remains true that cutting a small angle in half will also cut its tangent in half:

\[\tan(\frac{\pi}{2}) \quad \approx \quad \frac{1}{2}\tan(\pi)\]

and, in general, there is a linear relationship between the tiny angle π and its tangent, regardless of the units. Take a look for yourself:

Table 2

angle (degrees)	angle (radians)	tan(angle)
1	0.017453	0.017455
0.5	0.008727	0.008727
0.1	0.0017453	0.0017453
0.01	0.00017453	0.00017453

Okay, fine. Why am I belaboring this point? Because astronomers have chosen a set of units for parallax calculations which look strange, but turn out to simplify the actual work. The relationships between these units depend on the fact that there is a simple linear relationship between a tiny parallax angle, in ANY units, and the tangent of that angle.

angles are measured in arcseconds (")

Recall that 1 arcsecond = 1/3600 degree. Astronomers use arcseconds because parallax values for nearby stars are just a bit less than one arcsecond. You may also see angles quoted in mas, which stand for milli-arcseconds: 1 mas = 1/1000 arcsecond.

distances are measured in parsecs (pc)

A parsec is defined as the distance at which a star will have a heliocentric parallax half-angle of 1 arcsecond.

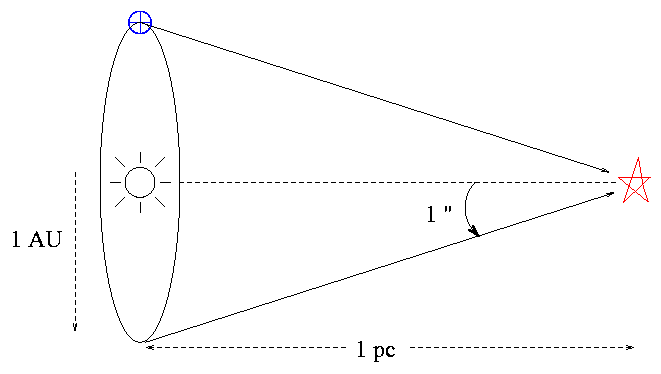
Exercise \(\PageIndex{1}\)

• How many meters are in one parsec?
• How many light years are in one parsec?

Given these units, and the linear relationship between a small angle and its tangent, we can calculate the distance to a star (in pc) very simply if we know its parallax half-angle in arcseconds:

\[ \mathsf{distance} \; (pc) = \frac{1}{\pi} \]

Give it a try: the first star to have its parallax measured accurately was 61 Cygni. Way back in 1838, the German astronomer Friedrich Bessel announced that its parallax half-angle was 0.314 arcseconds.

Exercise \(\PageIndex{2}\)

Based on Bessel's measuement, what is the distance to 61 Cygni?

Some observational difficulties

Actually, 1838 isn't all that long ago. Astronomers had been looking through telescopes since the time of Galileo, in the early 1600s. Why did it take over 200 years for someone to measure the parallax to another star?

There are several reasons:

• Really small. Smaller than the apparent size of stars as seen from the Earth's surface. Starlight is refracted by air as it passes through the Earth's atmosphere. It encounters layers with a range of temperatures and pressures, and, what's worse, all these layers are constantly in motion.
  • Schematic diagram of the atmosphere's effect on light

  As a result of all this refraction, astronomers on the ground perceive stars to be little blurry spots. The typical size of a "seeing disk" is around 1 arcsecond. In order to measure the parallax of a star, we must determine its position -- and that of several reference stars in the same field -- to a very small fraction of this seeing disk. That's not an easy task.

  • Look at examples of the observed shift in position
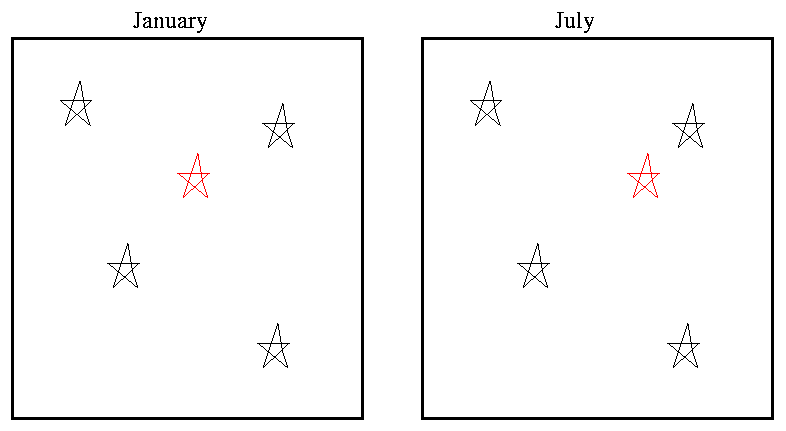
• In practice, astronomers usually measure the shift of one star in an image relative to other stars in the same image; differential measurements can be made much more precisely than absolute ones. However, as the Earth moves from one side of the Sun to the other, we will see ALL the stars in the field shift, not only the star of interest.

  In other words, we'd like to see this:

  

  But we instead some something like this:

  

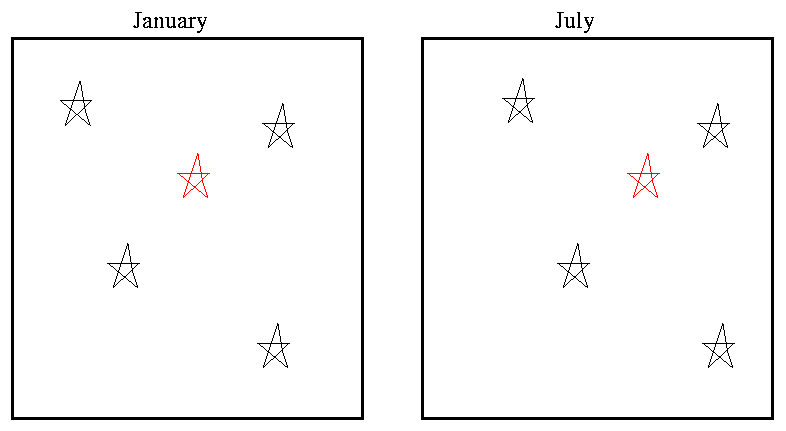
  The only hope is to pick out a set of reference stars which happen to be much farther away than the target star. Distant stars will shift by a much smaller angle -- perhaps small enough to be imperceptible. If we measure the position of the nearby target star relative to those distant ones, we might be able to detect its shift.

  In practice, astronomers perform a rather complicated series of computations:

  • pick a set of reference stars
  • estimate the distance to each reference star, using some method other than parallax
  • measure the shift of the target relative to the references
  • correct the position of each reference for its own parallactic shift
  • re-calculate the shift of the target, relative to these corrected reference positions

  How can we estimate the distance to the reference stars, if we haven't even determined the distance to the single target star yet? A good question. It requires a decades-long series of iterations:

  1. make a simple assumption, like "all stars are the same intrinsic luminosity, so apparent brightness is simply related to distance."
  2. use apparent brightness of reference stars to estimate their distances
  3. calculate the distance to the target star
  4. do this for hundreds of nearby target stars
  5. based on these measurements of distance to nearby stars, draw some general conclusions about the true luminosities of stars
  6. use these conclusions to make improved rules for estimating the distances to reference stars
  7. go to step 2
• We have to wait months for the Earth to move a significant distance in its orbit around the Sun. During that time, the Sun is moving through space at a decent clip: very roughly 12 km/s relative to nearby stars in the disk of the Milky Way. Other stars are moving, too, by similar speeds.

  Yes, most of the stars in the local neighborhood are orbiting around the center of the galaxy, at a speed of roughly 200 km/s. If all stars moved with EXACTLY the same velocity, we would see no relative motion as we all circled the Milky Way together. However, each star has some individual "peculiar velocity" relative to the average rotational velocity, and that is the velocity discussed here.

  There relative motions of the Sun and nearby stars produces proper motion: a gradual drift in the position of each star relative to all the others around it. These proper motions are in almost all cases so small that it takes thousands of years for the visual appearance of constellations to change:

  
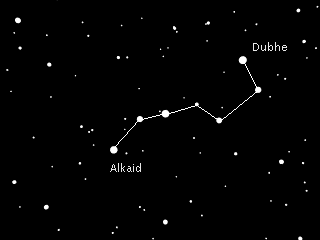
  Thanks to Anna Jangren at Wesleyan University

  However, the proper motions can be signficant at the level of precision required for parallax measurements. Consider these observations of Vega over a period of three years, made by the Hipparcos satellite.

  

  • Use this Java tool to plot the motions of any star observed by Hipparcos

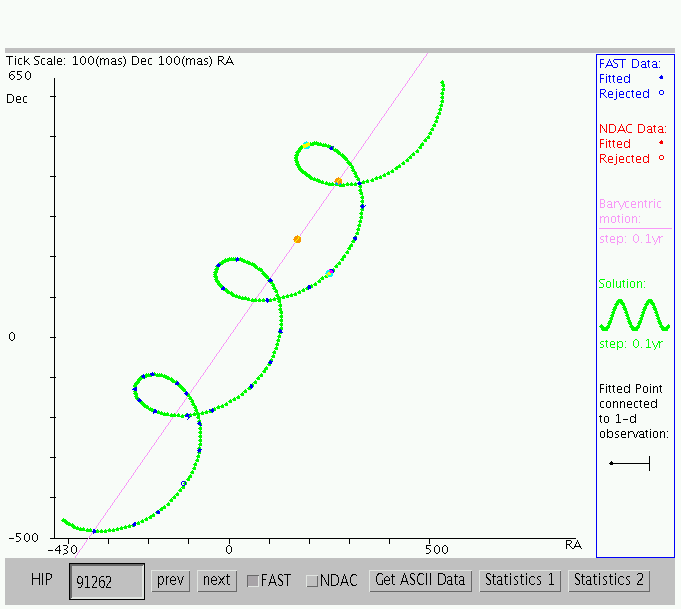
Exercise \(\PageIndex{3}\)

• What is the parallax of Vega?
• What is the distance to Vega?
• What is the proper motion of Vega, in arcsec/century?
• What is the tangential speed of Vega through space relative to the Sun?

Conlusions

The best large set of parallax measurements come from the Hipparcos satellite, which measured the position and brightness of relatively bright (brighter than tenth magnitude or so) stars over the entire sky during the period 1989-1993. A large team of scientists turned its millions of raw measurements into a consistent catalog of distances and luminosities.

• Access the catalog via the Hipparcos site's search tool
• To access the catalog via the Vizier service, which allows for more sophisticated searches, go to http://vizier.u-strasbg.fr/viz-bin/VizieR and type into the "Words matching author's name, etc." box

             I/239/hip_main/
         

  then press the "Find Catalogue" button.

The precision of the Hipparcos measurements of parallax is about 0.001 arcsecond. You might think that such precision would allow us to measure distances to stars as far away as 1000 pc. However, as we shall see, it turns out that the true range for accurate distances is quite a bit smaller.