13.2: Triangles
( \newcommand{\kernel}{\mathrm{null}\,}\)
I shall start with a geometric theorem involving triangles, which will be useful as we progress towards our aim of computing orbital elements.
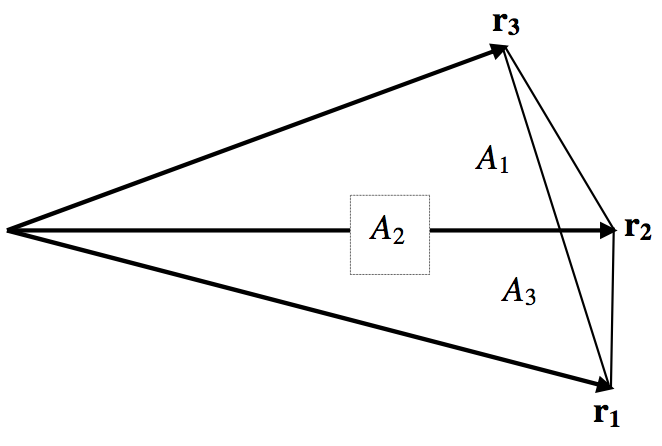
FIGURE XIII.1
Figure XIII.1 shows three coplanar vectors. It is clearly possible to express r2 as a linear combination of the other two. That is to say, it should be possible to find coefficients such that
r2=a1r1+a3r3.
The notation I am going to use is as follows:
- The area of the triangle formed by joining the tips of r2 and r3 is A1.
- The area of the triangle formed by joining the tips of r3 and r1 is A2.
- The area of the triangle formed by joining the tips of r1 and r2 is A3.
To find the coefficients in Equation ???, multiply both sides by r1×:
r1×r2=a3r1×r3.
The two vector products are parallel vectors (they are each perpendicular to the plane of the paper), of magnitudes 2A3 and 2A2 respectively. (2A3 is the area of the parallelogram of which the vectors r1 and r2 form two sides.)
∴
Similarly by multiplying both sides of Equation \ref{13.2.1} by \textbf{r}_3 \times it will be found that
a_1 = A_1/ A_2 . \label{13.2.4}
Hence we find that
A_2 \textbf{r}_2 = A_1 \textbf{r}_1 + A_3 \textbf{r}_3 . \label{13.2.5}


