11.1: Introduction to Curve of Growth
( \newcommand{\kernel}{\mathrm{null}\,}\)
The curve of growth (die Wachstumskurve) is a graph showing how the equivalent width of an absorption line, or the radiance of an emission line, increases with the number of atoms producing the line.
In an optically thin gas, the equivalent width of an absorption line, or the radiance of an emission line, is linearly proportional to the number of atoms in the initial level of the line. Let us imagine, for example, that we have a continuous source of radiation, and, in front of it, we have a homogeneous, isothermal slab of gas, and that there are N1 atoms per unit area in the line of sight in the lower level of some absorption line. We could double N1 either by doubling the thickness of the slab, or by doubling the density of the gas within the slab. Either way, if doubling the number of atoms per unit area (the column density) in level 1 results in a doubling of the equivalent width of the line, then the gas is said to be optically thin. More precisely, the line is optically thin – for there may well be other lines in the spectrum which are not optically thin. I suppose one could say that a gas is optically thin at the wavelength of a particular line if you can see all of the atoms – even those at the back. In Chapter 9, where we were developing formulas for the equivalent width of a line, and in Chapter 10, where we were studying line profiles, we were limiting our attention to optically thin lines. We shall depart from this assumption in this Chapter, although we shall still assume that our slab of gas is homogeneous (same temperature and pressure throughout) and in thermodynamic equilibrium.
We can see, by referring to figure XI.1, why it is that the equivalent width of an absorption line cannot continue to increase indefinitely and linearly as the column density increases. The figure represents the profile of an absorption line. (Strictly speaking, the ordinate should read “radiance per unit wavelength interval”, rather than “intensity”.) Profile a is a weak line (actually a gaussian profile) that is optically thin. In profile b, we have greatly increased the column density N1, and we see that the intensity at the centre of the line is almost zero. Hardly any of the background light from the continuous source is getting through. At this wavelength, the background is black. Increasing the column density will make no difference at all to the central intensity, and hardly any change in the equivalent width. Thus a graph of equivalent width versus column density will no longer be a linearly increasing function, but will be almost horizontal.
But it will not remain horizontal. As we see in profile c, when yet further atoms have been added, although the central depth does not and cannot become any deeper, the wings of the profile start to add to the equivalent width, so that the equivalent width starts to increase again, although rather more slowly than during the optically thin stage. Thus we might expect three stages in the curve of growth. At first, the equivalent width increases linearly with the column density of absorbers. Then there will be a stage in which the equivalent width is scarcely increasing. Finally, there will be a third stage in which the equivalent width increases, but not as rapidly as in the optically thin case.
It will also be noticed that, as soon as the profile (which was gaussian when it was optically thin) ceases to be optically thin, the profile becomes distorted and is no longer the same as it was in the optically thin region.
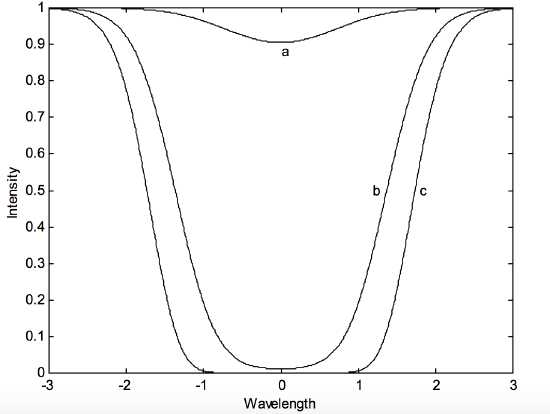
FIGURE XI.1
From our qualitative description of the curve of growth, it will be evident that the form of the curve of growth will depend on the form of the original line profile. For example, it will be recalled that the gaussian profile is “all core and no wings”, whereas the lorentzian profile is “narrow core and extensive wings”. Thus the onset of the third stage of the curve of growth will occur sooner for a lorentzian profile than for a gaussian profile. We shall find, as we proceed, that for a pure gaussian profile, the third stage of the classic curve of growth is scarcely evident, whereas for a pure lorentzian profile, the second stage is scarcely evident. The classic three-stage curve of growth is exhibited for a Voigt profile in which the gaussian and lorentzian contributions are comparable.
It will be part of the aim of this chapter to predict the curve of growth for gaussian and lorentzian profiles, and also for Voigt profile for different Gauss/Lorentz ratios.
This by itself will be an interesting intellectual exercise – but can it be taken further? Yes it can. Imagine a situation is which we have a spectrum in which the resolution is not sufficient to measure the profiles of individual lines with any great precision. No great imagination is in fact needed, for this will usually be the case with a stellar spectrum. If we can somehow construct a curve of growth, we might be able to deduce the line profiles, or at least the FWHm (full width at half minimum) of the gaussian component (which will tell us the kinetic temperature) and of the lorentzian component (which will tell us the mean time between collisions and hence the pressure). We cannot, of course, change the column density of a stellar atmosphere. However, some lines of a given element will be weak (because they have a high excitation potential, or a small oscillator strength, or both) and others will be strong (because they have a low excitation potential, or a large oscillator strength, or both), and perhaps a curve of growth can be constructed from many lines of a given atom, and so we will be able to deduce the temperature and the pressure, even though we cannot resolve the details of individual line profiles.
So far, I have discussed the curve of growth for an absorption line. What about an emission line? We understand that the intensity of the centre of an absorption line cannot drop below the “floor” corresponding to zero intensity. But is there a “ceiling” that will stop the growth of the centre of an emission line, or can we go on increasing the intensity of an emission line indefinitely? The answer is that, for a gas in thermodynamic equilibrium, there is indeed a “ceiling”, and that occurs when the radiance per unit wavelength interval of the centre of the emission line reaches the ordinate of the Planck blackbody curve having a blackbody temperature equal to the kinetic and excitation temperature of the gas. When the line centre is completely optically thick, it radiates like a black body at that wavelength. Adding more atoms to the column density will not increase the central intensity. What happens is that photons emitted by atoms near the back of the slab of gas are re-absorbed as they struggle forward towards the front.


