11.5: Curve of Growth for Lorentzian Profiles
( \newcommand{\kernel}{\mathrm{null}\,}\)
The optical depth of a line broadened by radiation damping is given, as a function of wavelength, by
τ(x)=τ(0)l2x2+l2,
where the HWHM is
l=Γλ204πc
and the optical thickness at the line center is
τ(0)=e2N1f12mϵ0cΓ.
Here x=λ−λ0, and the damping constant Γ may include a contribution from pressure broadening. As in Section 11.4, in figure XI.4 I draw line profiles for optical thicknesses at the line center τ(0)=116,18,14,12,1,2,4,8.
We see that the wings continue to add to the equivalent width as soon as, and indeed before, the central depth has reached unity. On combining equations 11.3.4, ???,2 and 3, we obtain the following expression for the equivalent width:
W=Γλ202πc∫∞0(1−exp{−τ(0)y2+1})dy,
in which y=x/l - i.e. distance from the line center in units of the HWHM.
If we now substitute y=tanθ, the expression for the equivalent width becomes
W=Γλ202πc∫π/201−exp[−τ(0)cos2θ]cos2θdθ.
Now that we have a finite upper limit, the expression can be integrated numerically without artificial and unjustified truncation. As described in the Appendix to Chapter 10, calculation of the trigonometric function cos can be avoided, and hence the integration much speeded up, by the substitution of t=tan(12θ). Although the denominator of the integrand is obviously zero at the upper limit, so is the numerator, and the value of the integrand at the upper limit is finite and equal to τ(0). Figure XI.5 shows the equivalent width, in units of Γλ202πc as a function of τ(0).
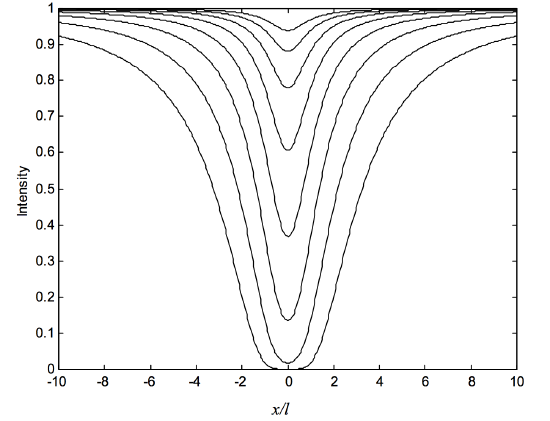
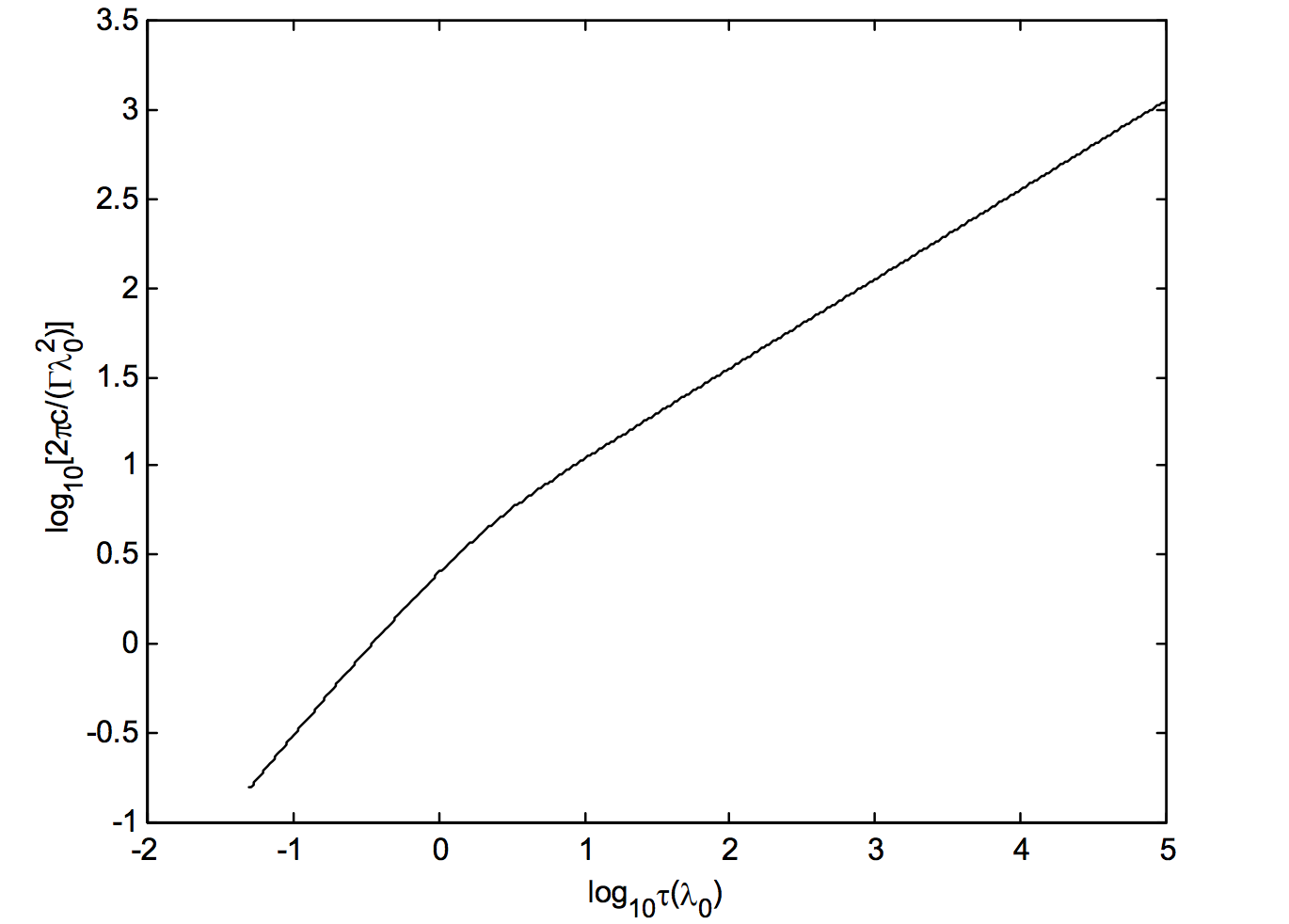
FIGURE XI.4 FIGURE XI.5


