6.2: Simple Models of the Atmosphere to Explain Limb Darkening
( \newcommand{\kernel}{\mathrm{null}\,}\)
1. The Sun consists of a spherical body emitting continuous blackbody radiation of radiance (specific intensity) Bν surrounded by a shallow ("plane parallel") atmosphere which absorbs light and is of optical thickness τ(ν) but does not emit. See figure VI.3.
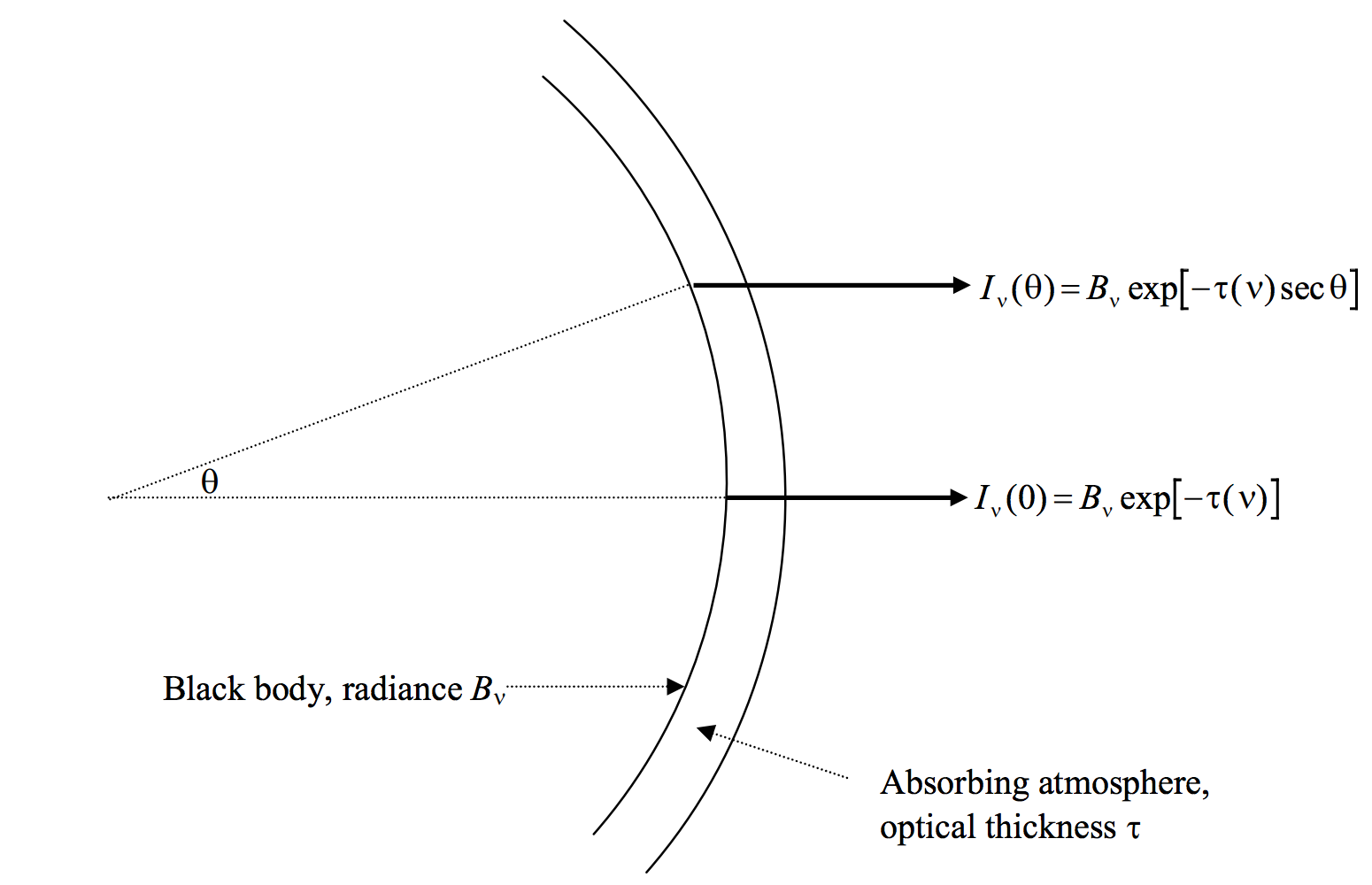
FIGURE VI.3
The emergent specific intensity at the centre of the disc is
Iν(0)=Bνe−τ(ν)
and at a position on the disc given by θ is
Iν(θ)=Bνe−τ(ν)secθ
so that the limb darkening is given by
Iν(θ)=Iv(0)e−τ(ν)(secθ−1)
If the limb darkening is indeed like this, then a graph of ln[Iν(θ)/Iν(θ)] versus 1−secθ will be a straight line whose slope will be the optical thickness of the atmosphere. However, in practice such a graph does not yield a straight line, and a comparison of Equation ???, which is shown in figure VI.4, with the observed limb darkening shown in figure VI.2, suggests that this is not at all a promising model.
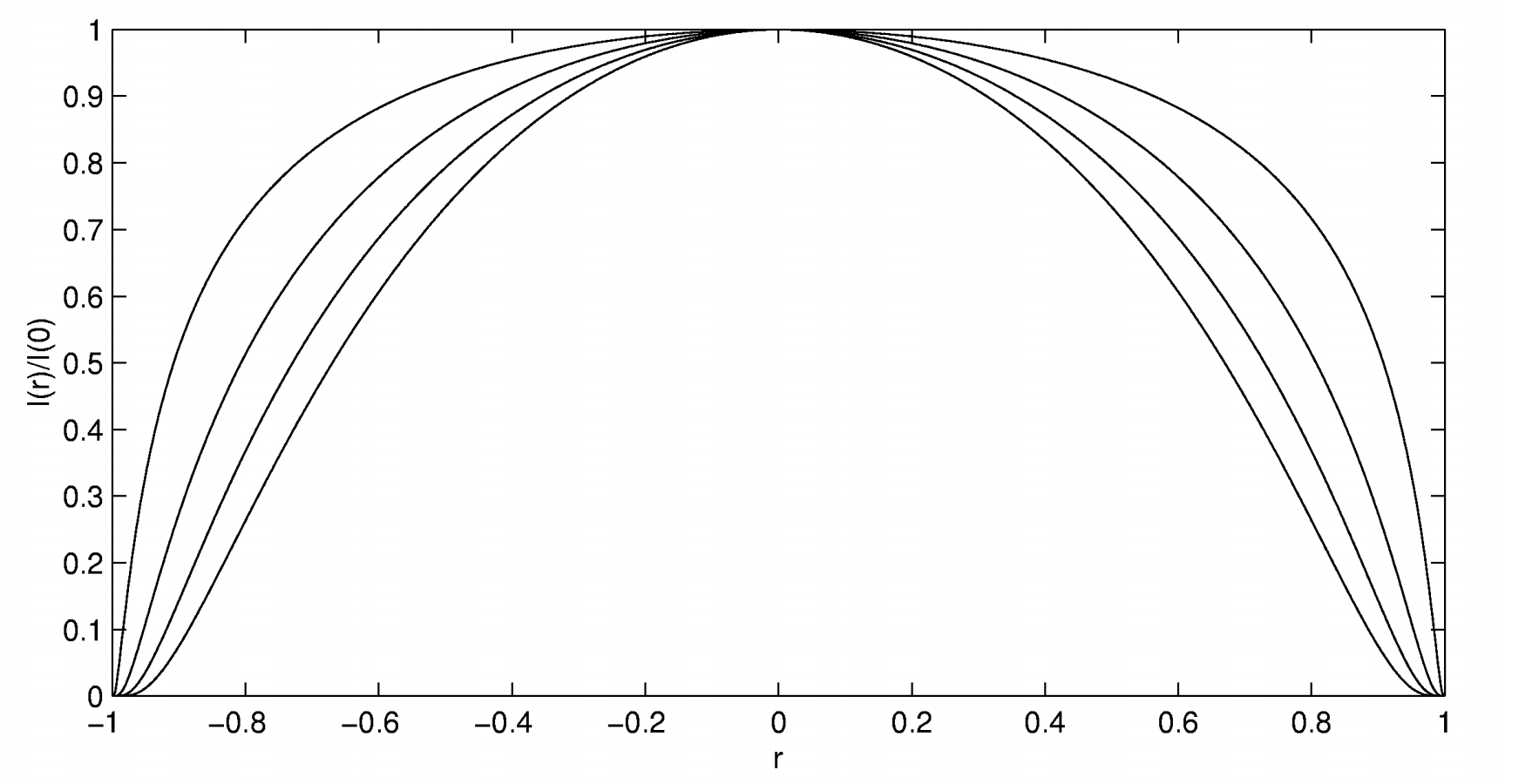
FIGURE VI.4
Equation ??? for four values of the optical thickness τ of the atmosphere. The curves are drawn for τ=0.2,0.4,0.6 and 0.8. The curves do not greatly resemble the empirical, observed curves of figure VI.2, suggesting that this is not a very good atmospheric model.
2. This second model is similar to the first model, except that the atmosphere emits radiation as well as absorbing it. We suppose that the surface of the Sun is a black body of specific intensity B1. The subscript 1 refers to the surface of the Sun. I have omitted a subscript ν. The argument is the same whether we are dealing with the specific intensity per unit frequency interval (Planck function) or the integrated specific intensity (Stefan's law). Suppose that the atmosphere, of optical thickness τ, is an emitting, absorbing atmosphere, of source function B2, being a Planck function corresponding to a cooler temperature than the surface. The emergent specific intensity will be the sum of the emergent intensity of the atmosphere (see Equation 5.7.2) and the specific intensity of the surface reduced by its passage through the atmosphere. At the centre of the disc, this will be
I(0)=B1e−τ+B2(1−e−τ)
and at a position θ on the disc it will be
I(θ)=B1e−τsecθ+B2(1−e−τsecθ)
and so the limb darkening will be given by
I(θ)I(0)=(B1−B2)e−τsecθ+B2(B1−B2)e−τ+B2
In attempting to find a good fit between Equation ??? and the observed limb darkening, we now have two adjustable parameters, τ and the ratio B2/B1. In figure VI.5 we show the limb darkening for τ=0.5,1.0, 1.5 and 2.0 for a representative ratio B2/B1=0.5. If we are dealing with radiation integrated over all wavelengths, this would imply an atmospheric temperature equal to (0.5)1/4=0.84 times the surface temperature. There is no combination of the two parameters that gives a limb darkening very similar to the observed limb darkening, so this model is not a specially good one.
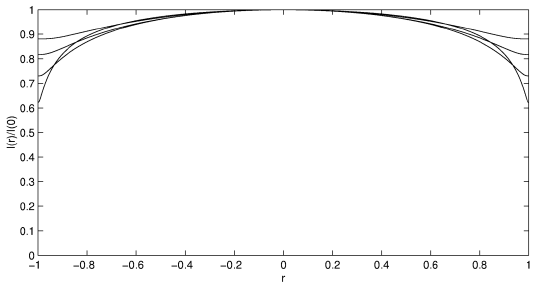
FIGURE VI.5
Equation ??? for B2/B1=0.5, and τ=0.5, 1.0, 1.5 and 2.0.
3. In this model we do not assume a hard and fast photosphere surrounded by an atmosphere of uniform source function; rather, we suppose that the source function varies continuously with depth. In figure VI.6 we draw two levels in the atmosphere, at optical depths τ and τ+dτ. The reader should recall that we are dealing only with a "plane parallel" atmosphere - i.e. one that is shallow compared with the radius of the star. The geometric distance between the two levels is therefore much exaggerated in the figure.
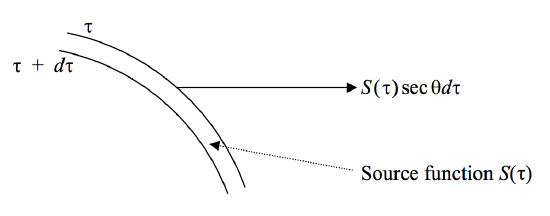
FIGURE VI.6
The source function of the shell between optical depths τ and τ+dτ is S(τ). In the direction θ the radiance (specific intensity) of an elemental shell of optical thickness dτ is S(τ)secθdτ.. (I have not explicitly indicated in this expression the dependence on frequency or wavelength of the source function or optical depth.) By the time the radiation from this shell reaches the outermost part of the atmosphere (i.e. where τ=0), it has been reduced by a factor e−τsecθ. The specific intensity resulting from the addition of all such elemental shells is
I(θ)=secθ∫∞0S(τ)e−τsecθdτ
This important Equation, attributed to Karl Schwarzschild, gives the limb darkening as a function of the way in which the source function varies with optical depth. The usual situation is that it is the limb darkening that is known and it is required to find S(τ), so that Equation ??? has to be solved as an integral Equation. This, however, is not as difficult as it may first appear because it will be noticed that if we write s=secθ, the Equation is merely a Laplace Transform:
I(s)=sL[S(τ)]
so that the source function is the inverse Laplace transform of the limb darkening.
If we assume that the source function can be expressed as a polynomial in the optical depth:
S(τ)=I(0)(a0+a1τ+a2τ2...)
we find for the limb darkening (remembering that 1/s=cosθ)
I(θ)=I(0)(a0+a1cosθ+2a2cos2θ...)
If we compare this with the empirical limb darkening Equation 6.1.3 we find the a coefficients in terms of the limb darkening coefficients, as follows:
a0=1−u′−ν′
a1=u′
a2=12ν′
If we extend this analysis a little further, we find that if the source function is given by
S(τ)=I(0)N∑0anτn
the limb darkening is
I(θ)=I(0)N∑0unμn
where μ=cosθ and it is left to the reader to determine a general relation between the an and the un.
If the limb darkening is given by Equation ???, calculate the mean specific intensity (radiance) ˉI over the solar disc in terms of I(0) and u. If the limb darkening is given by Equation ???, what is the mean specific intensity in terms of I(0), u′ and ν′? This is an important calculation because if, for example, you need to calculate the irradiance of a planet or a comet by the Sun, the intensity of the Sun is the mean radiance times the projected area of the solar disc


