6.1: Introduction. The Empirical Limb-darkening

The Sun is not equally bright all over, but it is darkened towards the limb. The effect is more pronounced at the blue end of the spectrum and less pronounced at the red. A reasonably good empirical representation of the form of the limb darkening is given by an equation for the specific intensity of the form

\[I(r) = I(0) \left[ 1 - u \left( 1 - \sqrt{\frac{a^2-r^2}{a^2}} \right) \right] \label{6.1.1}\]

Here, \(a\) is the radius of the solar disc, \(r\) is radial distance from the center of the disc and \(u\) is the limb darkening coefficient. This is often written in terms of \(\theta\) (see Figure \(\text{VI.1}\)) or of \(\mu = \cos \theta\):

\[\begin{align} I(\theta) &= I(0) \left[ 1-u(1-\cos \theta) \right] \\[5pt] &= I(0) [1-u(1-\mu)] \label{6.1.2} \end{align}\]

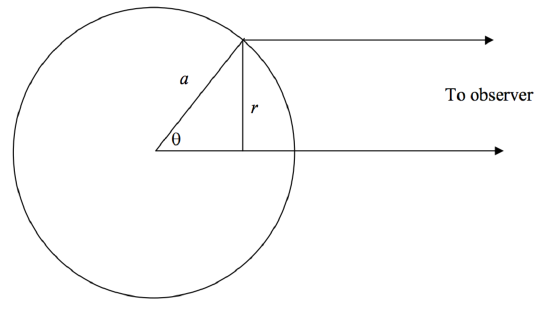
\(\text{FIGURE VI.1}\)

Whether written in the form of Equation \(\ref{6.1.1}\) or \(\ref{6.1.2}\), \(I(0)\) is the specific intensity at the center of the disc. The specific intensity at the limb (where \(r = a\) or \(\theta = 90^\circ\) ) is \(I(0)(1−u)\). The limb darkening coefficient can be written as

\[u = \dfrac{I(\text{center}) - I(\text{limb})}{I(\text{center})}.\]

Equation \(\ref{6.1.1}\) is shown in graphical form in figure \(\text{VI.2}\) for different values of the limb darkening coefficient.

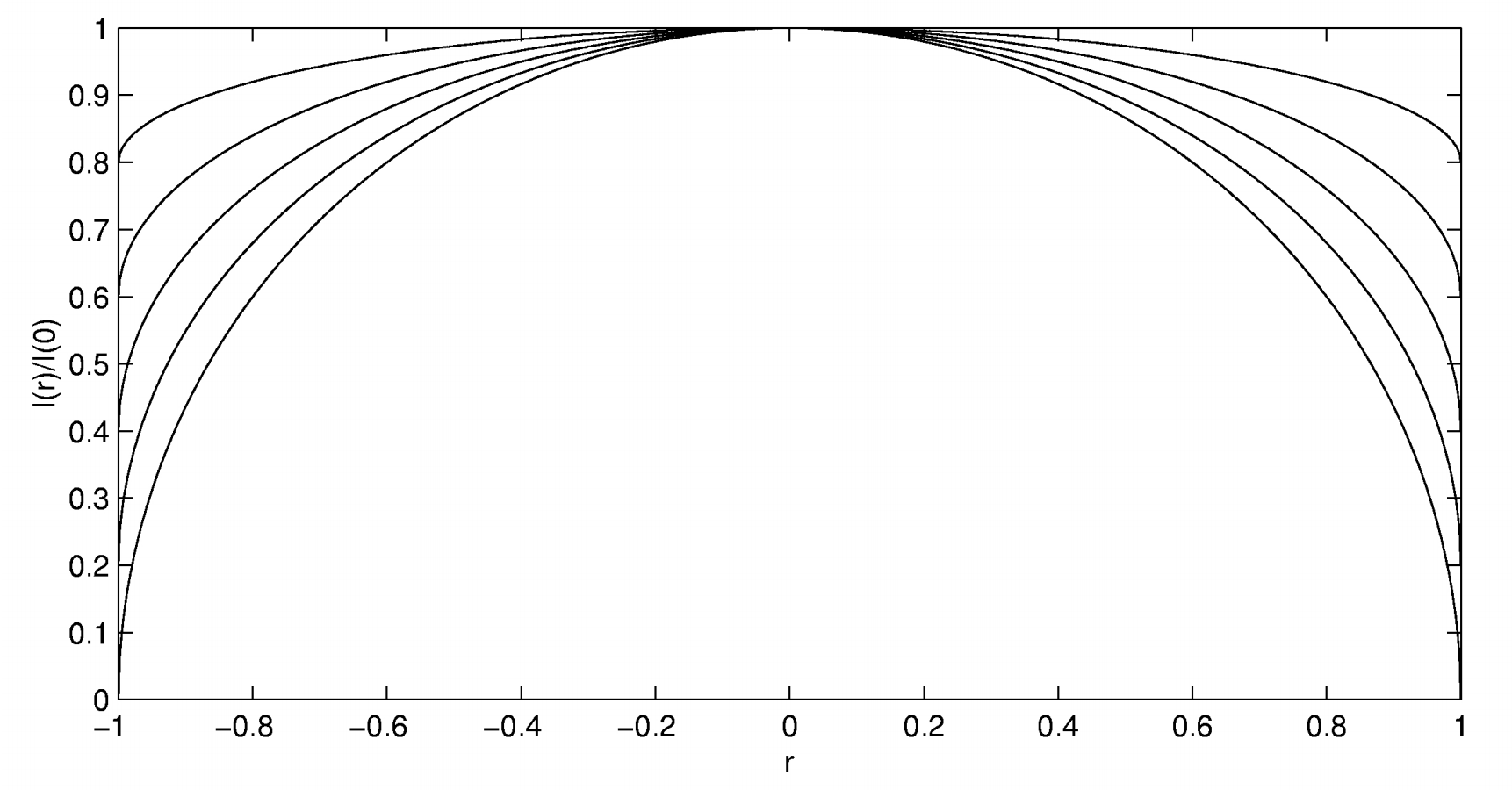
\(\text{FIGURE VI.2}\). Equation \(\ref{6.1.1}\) for six limb darkening coefficients, from the lowest curve upwards, \(u = 1.0, 0.8, 0.6, 0.4, 0.2 \ \text{and} \ 0.0\). The "curve" for the last of these (no limb darkening) is formed from three of the boundary lines. The curve for \(u = 1\) is a circle. The radius of the disc is taken to be \(1\), \(r = 0\) is the center of the disc and \(r = \pm 1\) is the limb.

Limb-darkening is much greater in the violet and near ultraviolet than in the red. For example, at a wavelength of \(600 \ \text{nm}\), \(u = 0.56\), whereas at \(320 \ \text{nm} \ u = 0.95\).

A slightly better empirical representation of the limb darkening can be obtained with two parameters, \(u^\prime\) and \(\nu^\prime\):

\[I(\theta) = I(0) \left[ 1 - u^\prime (1 - \cos \theta ) - \nu^\prime \sin^2 \theta \right] \label{6.1.3}\]

Why is the Sun darkened towards the limb?

We may perhaps imagine that the surface of the Sun radiates like a black body with uniform lambertian radiance, but it is surrounded by an absorbing atmosphere. Light from near the limb has to traverse a greater length of atmosphere than light from near the center of the disk and this accounts for the limb darkening. If that is the explanation, we should be able to calculate what form of limb darkening to expect, and see how well it agrees with what is observed. If the agreement is only moderately good, perhaps we could assume that the atmosphere is not only an absorbing atmosphere, but it also emits radiation of its own, and we could see if we could adjust the ratio of emission to extinction (the source function) to obtain good agreement with the model and the observations. Or perhaps, rather than thinking of a uniform radiating surface sharply separated from a surrounding atmosphere, we may imagine that there is no such sharp boundary, but, rather, the density and temperature of the solar gases increase continuously with depth. In that case, suppose that we can see everywhere to a given optical depth, say to \(\tau = 1\). Near the limb, an optical depth of unity does not take us very deep (in terms of kilometers) into the atmosphere, because we are looking almost tangentially at the surface of the Sun, so we reach only relatively high levels in the atmosphere where the temperature is relatively cool. Near the center, on the other hand, where we are peering down perpendicularly into the Sun, an optical depth of one reaches deep down (in terms of kilometers) to places where the atmosphere is very hot. Thus the center appears brighter than the limb.

At any rate, the point is that, by making precise measurements of the form of the limb darkening and comparing these measurements with the predictions of different models, we should in principle be able to deduce something about the run of density and temperature with optical depth in the atmosphere.

One practical difficulty of doing this is that it turns out that it is necessary to make quite precise measurements of the exact form of the limb darkening very close to the limb to be able to distinguish convincingly between different models.

Are there any prospects of being able to measure the limb darkening of stars other than the Sun? The future will tell whether advances in technology, such as adaptive optics, may enable us to observe the limb darkening of other stars directly. Other methods are possible. For example, the detailed light curve of an eclipsing binary star undoubtedly gives us information on the limb darkening of the star that is being eclipsed. There are many factors that affect the form of the light curve of an eclipsing binary star, and the detailed interpretation of light curves is not at all easy - but no one ever claimed that astronomy was easy. In principle lunar or asteroidal occultations of stars might enable us to determine the limb darkening of a star. Another possible method is from a careful examination of the line profiles in the spectrum of a rotating star. If a star is of uniform brightness and is rotating rapidly, the intensity profiles of its spectrum lines are broadened and have a semi-elliptical profile. However, if the star is darkened towards the limb, the line profile is affected. If the star's disk is completely limb darkened (\(u = 1\), so that the specific intensity at the limb is zero), it is an interesting exercise to show that the line profile is parabolic. For intermediate limb darkening, the profile is neither elliptical nor parabolic; an exact analysis of its shape could in principle tell us the limb darkening coefficient.