13.7: Power Applied by a Constant Force

Suppose that an applied force \(\overrightarrow{\mathbf{F}}^{a}\) acts on a body during a time interval \(\Delta t\) and the displacement of the point of application of the force is in the x -direction by an amount \(\Delta x\). The work done, \(\Delta W^{a}\), during this interval is

\[\Delta W^{a}=F_{x}^{a} \Delta x \nonumber \]

where \(F_{x}^{a}\) is the x -component of the applied force. (Equation (13.7.1) is the same as Equation (13.4.2).)

The average power of an applied force is defined to be the rate at which work is done,

\[P_{a v e}^{a}=\frac{\Delta W^{a}}{\Delta t}=\frac{F_{x}^{a} \Delta x}{\Delta t}=F_{x}^{a} v_{\text {ave }, x} \nonumber \]

The average power delivered to the body is equal to the component of the force in the direction of motion times the component of the average velocity of the body. Power is a scalar quantity and can be positive, zero, or negative depending on the sign of work. The SI units of power are called watts [W] and \([1 \mathrm{W}]=\left[1 \mathrm{J} \cdot \mathrm{s}^{-1}\right]\).

The instantaneous power at time t is defined to be the limit of the average power as the time interval \([t, t+\Delta t]\) approaches zero,

\[P^{a}=\lim _{\Delta t \rightarrow 0} \frac{\Delta W^{a}}{\Delta t}=\lim _{\Delta t \rightarrow 0} \frac{F_{x}^{a} \Delta x}{\Delta t}=F_{x}^{a}\left(\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}\right)=F_{x}^{a} v_{x} \nonumber \]

The instantaneous power of a constant applied force is the product of the component of the force in the direction of motion and the instantaneous velocity of the moving object.

Example \(\PageIndex{1}\): Gravitational Power for a Falling Object

Suppose a ball of mass \(m=0.2 \mathrm{kg}\) starts from rest at a height \(y_{0}=15 \mathrm{m}\) above the surface of the earth and falls down to a height \(y_{f}=5.0 \mathrm{m}\) above the surface of the earth. What is the average power exerted by the gravitation force? What is the instantaneous power when the ball is at a height \(y_{f}=5.0 \mathrm{m}\) above the surface of the Earth? Make a graph of power vs. time. You may ignore the effects of air resistance.

Solution

There are two ways to solve this problem. Both approaches require calculating the time interval \(\Delta t\) for the ball to fall. Set \(t_{0}=0\) for the time the ball was released. We can solve for the time interval \(\Delta t=t_{f}\) that it takes the ball to fall using the equation for a freely falling object that starts from rest,

\[y_{f}=y_{0}-\frac{1}{2} g t_{f}^{2} \nonumber \]

Thus the time interval for falling is

\[t_{f}=\sqrt{\frac{2}{g}\left(y_{0}-y_{f}\right)}=\sqrt{\frac{2}{9.8 \mathrm{m} \cdot \mathrm{s}^{-2}}(15 \mathrm{m}-5 \mathrm{m})}=1.4 \mathrm{s} \nonumber \]

First approach: we can calculate the work done by gravity,

\[\begin{aligned}
W^{g} &=-m g\left(y_{f}-y_{0}\right) \\
&=\left(-2.0 \times 10^{-1} \mathrm{kg}\right)\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(5 \mathrm{m}-15 \mathrm{m})=2.0 \times 10^{1} \mathrm{J}
\end{aligned} \nonumber \]

Then the average power is

\[P_{\text {ave }}^{g}=\frac{\Delta W}{\Delta t}=\frac{2.0 \times 10^{1} \mathrm{J}}{1.4 \mathrm{s}}=1.4 \times 10^{1} \mathrm{W} \nonumber \]

Second Approach. We calculate the gravitation force and the average velocity. The gravitation force is

\[F_{y}^{g}=-m g=-\left(2.0 \times 10^{-1} \mathrm{kg}\right)\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)=-2.0 \mathrm{N} \nonumber \]

The average velocity is

\[v_{\text {ave } y}=\frac{\Delta y}{\Delta t}=\frac{5 \mathrm{m}-15 \mathrm{m}}{1.4 \mathrm{s}}=-7.0 \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber \]

The average power is therefore

\[\begin{aligned}
P_{\text {ave }}^{g} &=F_{y}^{g} v_{\text {ave } y}=(-m g) v_{\text {ave }, y} \\
&=(-2.0 \mathrm{N})\left(-7.0 \mathrm{m} \cdot \mathrm{s}^{-1}\right)=1.4 \times 10^{1} \mathrm{W}
\end{aligned} \nonumber \]

In order to find the instantaneous power at any time, we need to find the instantaneous velocity at that time. The ball takes a time \(t_{f}=1.4 \mathrm{s}\) to reach the height \(y_{f}=5.0 \mathrm{m}\). The velocity at that height is given by

\[v_{y}=-g t_{f}=-\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(1.4 \mathrm{s})=-1.4 \times 10^{1} \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber \]

So the instantaneous power at time \(t_{f}=1.4 \mathrm{s}\) is

\[\begin{aligned}
P^{g} &=F_{y}^{g} v_{y}=(-m g)\left(-g t_{f}\right)=m g^{2} t_{f} \\
&=(0.2 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)^{2}(1.4 \mathrm{s})=2.7 \times 10^{1} \mathrm{W}
\end{aligned} \nonumber \]

If this problem were done symbolically, the answers given in Equation (13.7.11) and Equation (13.7.12) would differ by a factor of two; the answers have been rounded to two significant figures.

The instantaneous power grows linearly with time. The graph of power vs. time is shown in Figure 13.8. From the figure, it should be seen that the instantaneous power at any time is twice the average power between t = 0 and that time.

Figure 13.8 Graph of power vs. time

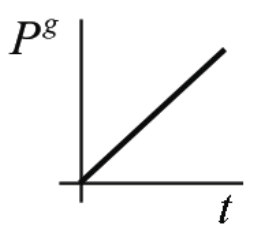
Example \(\PageIndex{2}\): Power Pushing a Cup

A person pushes a cup of mass 0.2 kg along a horizontal table with a force of magnitude 2.0 N at an angle of \(30^{\circ}\) with respect to the horizontal for a distance of 0.5 m , as in Example 13.4. The coefficient of friction between the table and the cup is \(\mu_{k}=0.1\). What is the average power of the pushing force? What is the average power of the kinetic friction force?

Solution

We will use the results from Examples 13.4 and 13.7 but keeping extra significant figures in the intermediate calculations. The work done by the pushing force is

\[W^{a}=F_{x}^{a}\left(x_{f}-x_{0}\right)=(1.732 \mathrm{N})(0.50 \mathrm{m})=8.660 \times 10^{-1} \mathrm{J} \nonumber \]

The final speed of the cup is \(v_{x, f}=2.860 \mathrm{m} \cdot \mathrm{s}^{-1}\). Assuming constant acceleration, the time during which the cup was pushed is

\[t_{f}=\frac{2\left(x_{f}-x_{0}\right)}{v_{x, f}}=0.3496 \mathrm{s} \nonumber \]

The average power of the pushing force is then, with \(\Delta t=t_{f}\),

\[P_{\text {ave }}^{a}=\frac{\Delta W^{a}}{\Delta t}=\frac{8.660 \times 10^{-1} \mathrm{J}}{0.3496 \mathrm{s}}=2.340 \mathrm{W} \nonumber \]

or 2.3W to two significant figures. The work done by the friction force is

\[\begin{aligned}
W^{f} &=f_{\mathrm{k}}\left(x_{f}-x_{0}\right) \\
&=-\mu_{\mathrm{k}} N\left(x_{f}-x_{0}\right)=-\left(9.6 \times 10^{-2} \mathrm{N}\right)(0.50 \mathrm{m})=-\left(4.8 \times 10^{-2} \mathrm{J}\right)
\end{aligned} \nonumber \]

The average power of kinetic friction is

\[P_{\text {ave }}^{f}=\frac{\Delta W^{f}}{\Delta t}=\frac{-4.8 \times 10^{-2} \mathrm{J}}{0.3496 \mathrm{s}}=-1.4 \times 10^{-1} \mathrm{W} \nonumber \]

The time rate of change of the kinetic energy for a body of mass m moving in the x-direction is

\[\frac{d K}{d t}=\frac{d}{d t}\left(\frac{1}{2} m v_{x}^{2}\right)=m \frac{d v_{x}}{d t} v_{x}=m a_{x} v_{x} \nonumber \]

By Newton’s Second Law, \(F_{x}=m a_{x}\) and so Equation (13.7.18) becomes

\[\frac{d K}{d t}=F_{x} v_{x}=P \nonumber \]

The instantaneous power delivered to the body is equal to the time rate of change of the kinetic energy of the body.