13.8: Work and the Scalar Product

We shall introduce a vector operation, called the scalar product or “dot product” that takes any two vectors and generates a scalar quantity (a number). We shall see that the physical concept of work can be mathematically described by the scalar product between the force and the displacement vectors.

Scalar Product

Let $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ be two vectors. Because any two non-collinear vectors form a plane, we define the angle θ to be the angle between the vectors $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ as shown in Figure 13.9. Note that θ can vary from 0 to $\pi$.

Figure 13.9 Scalar product geometry.

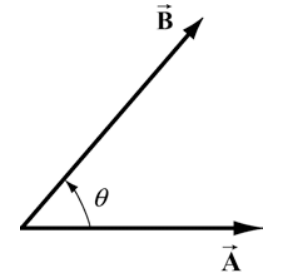
The scalar product $\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}$ of the vectors $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ is defined to be product of the magnitude of the vectors $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ with the cosine of the angle θ between the two vectors:

$$\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A B \cos (\theta) \nonumber$$

where $A=|\overrightarrow{\mathbf{A}}| \text { and } B=\mid \overrightarrow{\mathbf{B}}$ represent the magnitude of $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ respectively. The scalar product can be positive, zero, or negative, depending on the value of $\cos \theta$. The scalar product is always a scalar quantity.

The angle formed by two vectors is therefore

$$\theta=\cos ^{-1}\left(\frac{\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}}{|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{B}}|}\right) \nonumber$$

The magnitude of a vector $\overrightarrow{\mathbf{A}}$ is given by the square root of the scalar product of the vector $\overrightarrow{\mathbf{A}}$ with itself.

$$|\overrightarrow{\mathbf{A}}|=(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})^{1 / 2} \nonumber$$

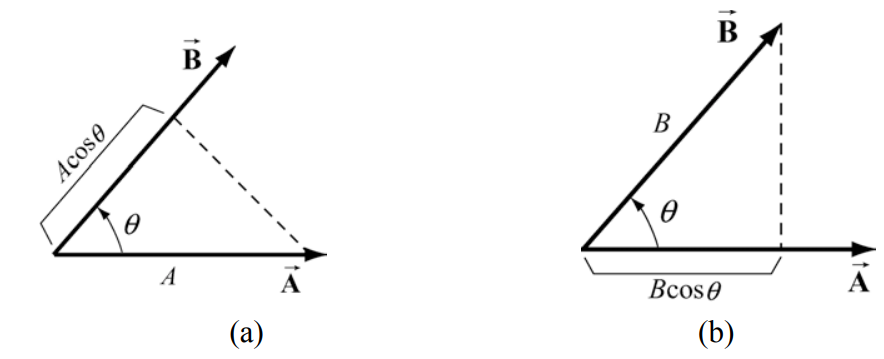
We can give a geometric interpretation to the scalar product by writing the definition as

$$\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=(A \cos (\theta)) B \nonumber$$

In this formulation, the term Acosθ is the projection of the vector $\overrightarrow{\mathbf{B}}$ in the direction of the vector $\overrightarrow{\mathbf{B}}$. This projection is shown in Figure 13.10a. So the scalar product is the product of the projection of the length of $\overrightarrow{\mathbf{A}}$ in the direction of $\overrightarrow{\mathbf{B}}$ with the length of $\overrightarrow{\mathbf{B}}$. Note that we could also write the scalar product as

$$\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A(B \cos (\theta)) \nonumber$$

Now the term $B \cos (\theta)$ is the projection of the vector $\overrightarrow{\mathbf{B}}$ in the direction of the vector $\overrightarrow{\mathbf{A}}$ as shown in Figure 13.10b. From this perspective, the scalar product is the product of the projection of the length of $\overrightarrow{\mathbf{B}}$ in the direction of $\overrightarrow{\mathbf{A}}$ with the length of $\overrightarrow{\mathbf{A}}$.

Figure 13.10 (a) and (b) Projection of vectors and the scalar product

From our definition of the scalar product we see that the scalar product of two vectors that are perpendicular to each other is zero since the angle between the vectors is $\pi / 2$ and $\cos (\pi / 2)=0$.

We can calculate the scalar product between two vectors in a Cartesian coordinates system as follows. Consider two vectors $\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}}$ and $\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}}+B_{y} \hat{\mathbf{j}}+B_{z} \hat{\mathbf{k}}$. Recall that

$$\begin{array}{l} \hat{\mathbf{i}} \cdot \hat{\mathbf{i}}=\hat{\mathbf{j}} \cdot \hat{\mathbf{j}}=\hat{\mathbf{k}} \cdot \hat{\mathbf{k}}=1 \\ \hat{\mathbf{i}} \cdot \hat{\mathbf{j}}=\hat{\mathbf{j}} \cdot \hat{\mathbf{k}}=\hat{\mathbf{i}} \cdot \hat{\mathbf{k}}=0 \end{array} \nonumber$$

The scalar product between $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ is then

$$\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z} \nonumber$$

The time derivative of the scalar product of two vectors is given by

$$\begin{array}{l} \frac{d}{d t}(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}})=\frac{d}{d t}\left(A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}\right) \\ =\frac{d}{d t}\left(A_{x}\right) B_{x}+\frac{d}{d t}\left(A_{y}\right) B_{y}+\frac{d}{d t}\left(A_{z}\right) B_{z}+A_{x} \frac{d}{d t}\left(B_{x}\right)+A_{y} \frac{d}{d t}\left(B_{y}\right)+A_{z} \frac{d}{d t}\left(B_{z}\right) \\ =\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right) \cdot \overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{A}} \cdot\left(\frac{d}{d t} \overrightarrow{\mathbf{B}}\right) \end{array} \nonumber$$

In particular when $\overrightarrow{\mathbf{A}}=\overrightarrow{\mathbf{B}}$, then the time derivative of the square of the magnitude of the vector $\overrightarrow{\mathbf{A}}$ is given by

$$\frac{d}{d t} A^{2}=\frac{d}{d t}(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})=\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right) \cdot \overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{A}} \cdot\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right)=2\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right) \cdot \overrightarrow{\mathbf{A}} \nonumber$$

Kinetic Energy and the Scalar Product

For an object undergoing three-dimensional motion, the velocity of the object in Cartesian components is given by $\overrightarrow{\mathbf{v}}=v_{x} \hat{\mathbf{i}}+v_{y} \hat{\mathbf{j}}+v_{z} \hat{\mathbf{k}}$. Recall that the magnitude of a vector is given by the square root of the scalar product of the vector with itself,

$$A \equiv|\overrightarrow{\mathbf{A}}| \equiv(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{A}})^{1 / 2}=\left(A_{x}^{2}+A_{y}^{2}+A_{z}^{2}\right)^{1 / 2} \nonumber$$

Therefore the square of the magnitude of the velocity is given by the expression

$$v^{2} \equiv(\overrightarrow{\mathbf{v}} \cdot \overrightarrow{\mathbf{v}})=v_{x}^{2}+v_{y}^{2}+v_{z}^{2} \nonumber$$

Hence the kinetic energy of the object is given by

$$K=\frac{1}{2} m(\overrightarrow{\mathbf{v}} \cdot \overrightarrow{\mathbf{v}})=\frac{1}{2} m\left(v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\right) \nonumber$$

Work and the Scalar Product

Work is an important physical example of the mathematical operation of taking the scalar product between two vectors. Recall that when a constant force acts on a body and the point of application of the force undergoes a displacement along the x -axis, only the component of the force along that direction contributes to the work,

$$W=F_{x} \Delta x \nonumber$$

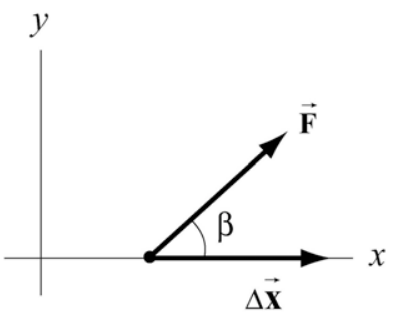
Suppose we are pulling a body along a horizontal surface with a force $\overrightarrow{\mathbf{F}}$. Choose coordinates such that horizontal direction is the x -axis and the force $\overrightarrow{\mathbf{F}}$ forms an angle $\beta$ with the positive x -direction. In Figure 13.11 we show the force vector $\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}+F_{y} \hat{\mathbf{j}}$ and the displacement vector of the point of application of the force $\Delta \overrightarrow{\mathbf{x}}=\Delta x \hat{\mathbf{i}}$. Note that $\Delta \overrightarrow{\mathbf{x}}=\Delta x \hat{\mathbf{i}}$ is the component of the displacement and hence can be greater, equal, or less than zero (but is shown as greater than zero in the figure for clarity). The scalar product between the force vector $\overrightarrow{\mathbf{F}}$ and the displacement vector $\Delta \overrightarrow{\mathbf{x}}$ is

$$\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}}=\left(F_{x} \hat{\mathbf{i}}+F_{y} \hat{\mathbf{j}}\right) \cdot(\Delta x \hat{\mathbf{i}})=F_{x} \Delta x \nonumber$$

Figure 13.11 Force and displacement vectors

The work done by the force is then

$$\Delta W=\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}} \nonumber$$

In general, the angle $\beta$ takes values within the range $-\pi \leq \beta \leq \pi$ (in Figure 13.11, $0 \leq \beta \leq \pi / 2$). Because the x -component of the force is $F_{x}=F \cos (\beta)$ where $F=|\overrightarrow{\mathbf{F}}|$ denotes the magnitude of $\overrightarrow{\mathbf{F}}$, the work done by the force is

$$W=\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}}=(F \cos (\beta)) \Delta x \nonumber$$

Example 13.10 Object Sliding Down an Inclined Plane

An object of mass m = 4.0 kg , starting from rest, slides down an inclined plane of length l = 3.0 m . The plane is inclined by an angle of $\theta=30^{\circ}$ to the ground. The coefficient of kinetic friction is $\mu_{k}=0.2$ (a) What is the work done by each of the three forces while the object is sliding down the inclined plane? (b) For each force, is the work done by the force positive or negative? (c) What is the sum of the work done by the three forces? Is this positive or negative?

Solution: (a) and (b) Choose a coordinate system with the origin at the top of the inclined plane and the positive x -direction pointing down the inclined plane, and the positive y - direction pointing towards the upper right as shown in Figure 13.12. While the object is sliding down the inclined plane, three uniform forces act on the object, the gravitational force which points downward and has magnitude $F_{g}=m g$, the normal force N which is perpendicular to the surface of the inclined plane, and the friction force which opposes the motion and is equal in magnitude to $f_{k}=\mu_{k} N$. A force diagram on the object is shown in Figure 13.13.

Figure 13.12 Coordinate system for object sliding down the inclined plane

Figure 13.13 Free-body force diagram for object

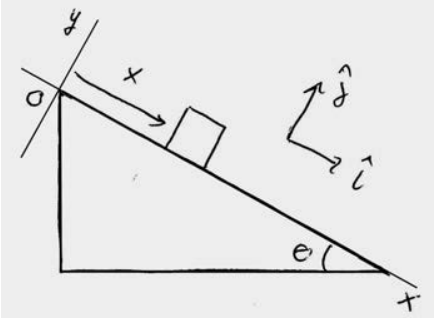
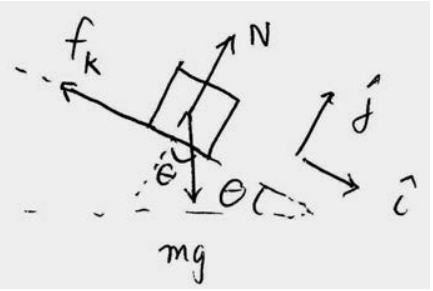
In order to calculate the work we need to determine which forces have a component in the direction of the displacement. Only the component of the gravitational force along the positive x -direction $F_{g x}=m g \sin \theta$ and the friction force are directed along the displacement and therefore contribute to the work. We need to use Newton’s Second Law to determine the magnitudes of the normal force. Because the object is constrained to move along the positive x -direction, $a_{y}=0$, Newton’s Second Law in the $\hat{\mathbf{j}}$-direction $N-m g \cos \theta=0$. Therefore $N=m g \cos \theta$ and the magnitude of the friction force is $f_{k}=\mu_{k} m g \cos \theta$.

With our choice of coordinate system with the origin at the top of the inclined plane and the positive x -direction pointing down the inclined plane, the displacement of the object is given by the vector $\Delta \overrightarrow{\mathbf{r}}=\Delta x \hat{\mathbf{i}}$ (Figure 13.14).

Figure 13.14 Force vectors and displacement vector for object

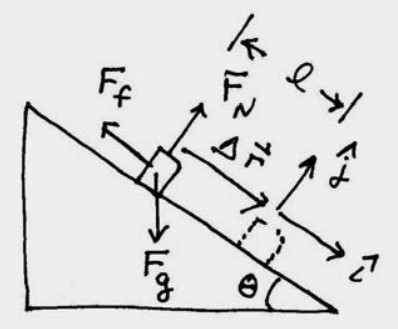
The vector decomposition of the three forces are $\overrightarrow{\mathbf{F}}^{g}=m g \sin \theta \hat{\mathbf{i}}-m g \cos \theta \hat{\mathbf{j}}$, $\overrightarrow{\mathbf{F}}^{f}=-\mu_{k} m g \cos \theta \hat{\mathbf{i}}$, and $\overrightarrow{\mathbf{F}}^{N}=m g \cos \theta \hat{\mathbf{j}}$. The work done by the normal force is zero because the normal force is perpendicular the displacement

$$W^{N}=\overrightarrow{\mathbf{F}}^{N} \cdot \Delta \overrightarrow{\mathbf{r}}=m g \cos \theta \hat{\mathbf{j}} \cdot l \hat{\mathbf{i}}=0 \nonumber$$

Then the work done by the friction force is negative and given by

$$W^{f}=\overrightarrow{\mathbf{F}}^{f} \cdot \Delta \overrightarrow{\mathbf{r}}=-\mu_{k} m g \cos \theta \hat{\mathbf{i}} \cdot l \hat{\mathbf{i}}=-\mu_{k} m g \cos \theta l<0 \nonumber$$

Substituting in the appropriate values yields

$$W^{f}=-\mu_{k} m g \cos \theta l=-(0.2)(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(3.0 \mathrm{m})\left(\cos \left(30^{\circ}\right)(3.0 \mathrm{m})=-20.4 \mathrm{J}\right. \nonumber$$

The work done by the gravitational force is positive and given by

$$W^{g}=\overrightarrow{\mathbf{F}}^{g} \cdot \Delta \overrightarrow{\mathbf{r}}=(m g \sin \theta \hat{\mathbf{i}}-m g \cos \theta \hat{\mathbf{j}}) \cdot l \hat{\mathbf{i}}=m g l \sin \theta>0 \nonumber$$

Substituting in the appropriate values yields

$$W^{g}=m g l \sin \theta=(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(3.0 \mathrm{m})\left(\sin \left(30^{\circ}\right)=58.8 \mathrm{J}\right. \nonumber$$

(c) The scalar sum of the work done by the three forces is then

$$\begin{array}{l} W=W^{g}+W^{f}=m g l\left(\sin \theta-\mu_{k} \cos \theta\right) \\ W=(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(3.0 \mathrm{m})\left(\sin \left(30^{\circ}\right)-(0.2)\left(\cos \left(30^{\circ}\right)\right)=38.4 \mathrm{J} .\right. \end{array} \nonumber$$