3.4: Notation
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section I am going to suppose that we n particles scattered through three-dimensional space. We shall be deriving some general properties and theorems – and, to the extent that a solid body can be considered to be made up of a system of particles, these properties and theorems will apply equally to a solid body.
In the Figure III.5, I have drawn just two of the particles, (the rest of them are left to your imagination) and the centre of mass C of the system.
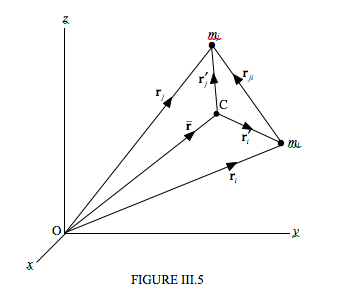
A given particle may have an external force Fi acting upon it. (It may, of course, have several external forces acting on it, but I mean by Fi the vector sum of all the external forces acting on the i th particle.) It may also interact with the other particles in the system, and consequently it may have internal forces Fij acting upon it, where j goes from 1 to n except for i. I define the vector sum F=∑Fi as the total external force acting upon the system.
I am going to establish the following notation for the purposes of this chapter.
- Mass of the i th particle = mi
- Total mass of the system M=∑mi
- Position vector of the i th particle referred to a fixed point O: ri=xiˆx+yiˆy+ziˆz
- Velocity of the i th particle referred to a fixed point O: ri or vi (Speed = vi)
- Linear momentum of the i th particle referred to a fixed point O: pi=mivi
- Linear momentum of the system: P=∑Pi=∑mivi
- External force on the i th particle: Fi
- Total external force on the system: F=∑Fi
- Angular momentum (moment of momentum) of the i th particle referred to a fixed point O: li=ri×pi
- Angular momentum of the system: L=∑li=∑ri×pi
- Torque on the i th particle referred to a fixed point O: τi=ri×Fi
- Total external torque on the system with respect to the origin: τ=∑τi=∑ri×Fi
Kinetic energy of the system: (We are dealing with a system of particles – so we are dealing only with translational kinetic energy – no rotation or vibration):
T=∑12miv2i
Position vector of the centre of mass referred to a fixed point O: ¯ri=¯xˆx+¯yˆy+¯zˆz
The centre of mass is defined by M¯r=∑miri
Velocity of the centre of mass referred to a fixed point O: ¯r=¯v (Speed = ¯v )
For position vectors, unprimed single-subscript symbols will refer to O. Primed single-subscript symbols will refer to C. This will be clear, I hope, from Figure III.5.
Position vector of the i th particle referred to the centre of mass C: r′i=ri−¯ri
Position vector of particle j with respect to particle i: rij=rj−ri
(Internal) force exerted on particle i by particle j: Fij
(Internal) force exerted on particle j by particle i: Fji
If the force between two particles is repulsive (e.g. between electrically-charged particles of the same sign), then Fji and rji are in the same direction. But if the force is an attractive force, Fji and rji are in opposite directions.
According to Newton’s Third Law of Motion (Lex III), Fij=−Fji
Total angular momentum of system referred to the centre of mass C: LC
Total external torque on system referred to the centre of mass C: τC
For the velocity of the centre of mass I may use either ˙¯r or ¯v
O is an arbitrary origin of coordinates. C is the centre of mass.
Note that
ri=¯r+r′i
and therefore
˙¯ri=˙¯r+˙r′i;
that is to say
vi=¯v+v′i
Note also that
∑mir′i=0
Note further that
∑miv′i=∑mi(vi−¯v)=∑mivi−¯v∑mi=M¯v−¯vM=0
That is, the total linear momentum with respect to the centre of mass is zero.
Having established our notation, we now move on to some theorems concerning systems of particles. It may be more useful for you to conjure up a physical picture in your mind what the following theorems mean than to memorize the details of the derivations.


