4.6: Force-free Motion of a Rigid Asymmetric Top
( \newcommand{\kernel}{\mathrm{null}\,}\)
By “asymmetric top” I mean a body whose three principal moments of inertia are unequal. While we often think of a “top” as a symmetric body spinning on a table, in this section the “top” will not necessarily be symmetric, and it will not be in contact with any table, nor indeed subjected to any external forces or torques.
A complete description of the motion of an asymmetric top is quite complicated, and therefore all that we shall attempt in this chapter is a qualitative description of certain aspects of the motion. That our description is going to be “qualitative” does not by any means imply that this section is not going to be replete with equations or that we can give our poor brains a rest.
The first point that we can make is that, provided that no external torques act on the body, its angular momentum L is constant in magnitude and direction. A second point is that, provided the body is rigid and has no internal degrees of freedom, the rotational kinetic energy T is constant. I deal briefly with nonrigid bodies in Section 4.7. Although the angular velocity vector ω is by no means fixed in either magnitude and direction, and the body can tumble over and over, these two conditions impose some constraints of the magnitude and direction of ω.
We are going to examine these two conditions to see what constraints are imposed on ω. One of the things we shall find is that rotation of a body about a principal axis of greatest or of least moment of inertia is stable against small displacements, whereas rotation about the principal axis of intermediate moment of inertia is unstable.
Absence of an external torque means that the angular momentum is constant:
L2=L21+L22+L23=constant,
so that, at all times,
I21ω21+I22ω22+I23ω23=L2
Thus, for a given L. the angular velocity components always satisfy
ω21(L/I1)2+ω22(L/I2)2+ω23(L/I3)2=1.
That is to say, the angular velocity vector is constrained such that the tip of the vector ω is always on the surface of an ellipsoid of semi axes LI1, LI2, LI3,
In addition to the constancy of angular momentum, the kinetic energy is also constant:
12I1ω21+12I2ω22+12I3ω23=T
Thus the tip of the angular velocity vector must also be on the surface of the ellipsoid
ω21(√2T/I1)2+ω22(√2T/I2)2+ω23(√2T/I3)2=1.
This ellipsoid (which is similar in shape to the momental ellipsoid) has semi axes √2T/I1,√2T/I2,√2T/I3.
Thus, how ever the body tumbles over and over, ω is constrained in magnitude and direction so that its tip is on the curve where these two ellipses intersect.
Suppose, that we have a rigid body with
- I1 = 0.2 kgm2
- I2 = 0.3 kgm2
- I3 = 0.5 kgm2
and that we set it in motion such that the angular momentum and kinetic energy are L = 4 J s and T = 20 J.
(The angular momentum and kinetic energy will be determined by the magnitude and direction of the initial velocity vector by which it is set in motion.)
The tip of ω is constrained to be on the curve of intersection of the two ellipsoids
ω21202+ω2213.32+ω2382=1
and
ω2114.142+ω2211.552+ω238.942=1
It is not easy (or I do not find it so) to imagine what this curve of intersection looks like in three-dimensional space, but one of my students, Leif Petersen, prepared the drawing below, and I am grateful to him for permission to reproduce it here. You can see that the curve of intersection is not a plane curve.
In case it’s of any help, you might want to note that equations 4.6.6 and 4.6.7 can be written
4ω21+9ω22+25ω23=1600
and
2ω21+3ω22+5ω23=400
but I’m going to leave the equations in the form 4.6.6 and 4.6.7, and in figure IV.7, I’ll sketch one octant of the two ellipsoidal surfaces.
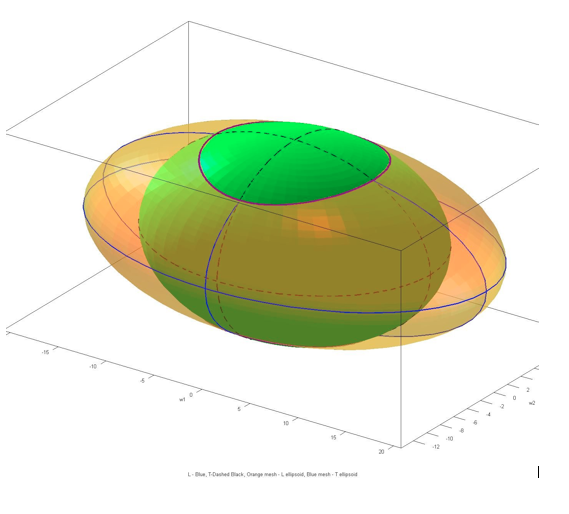
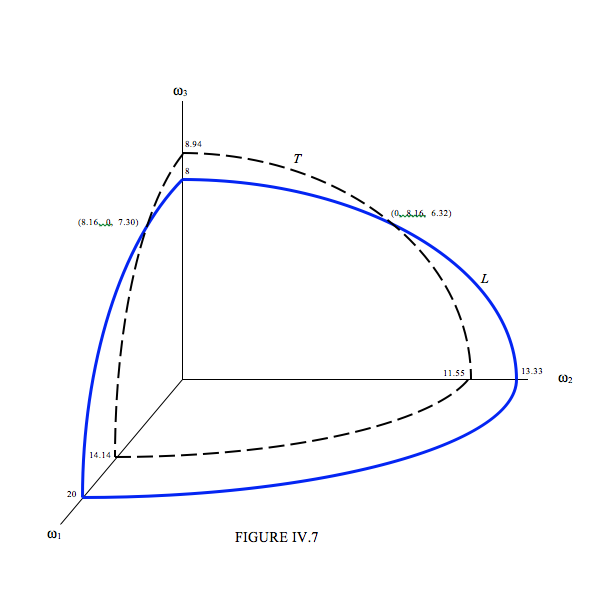
The continuous blue curve shows an octant of the ellipsoid L = constant, and the dashed black curve shows an octant of the ellipsoid T = constant. The angular momentum vector can end only on the curve (not drawn) where the two ellipsoids intersect. Two points on the curve are indicated in Figure IV.7. If, for example, ω is oriented so that ω1 = 0, the other two components must be ω2 = 8.16 and ω3 = 6.32. If it is oriented so that ω3 = 0, the other two components must be ω3 = 7.30 and ω1 = 8.16. If ω3 = 0, there are no real solutions for ω1 and ω2. This means that, for the given values of L and T, ω3 cannot be zero.
Now I’m going to address myself to the stability of rotation when a symmetric top is initially set to spin about one of its principal axes, which I’ll take to be the z-axis. We’ll suppose that initially ω1 = ω2 = 0, and ω3 = Ω. In that case the angular momentum and the kinetic energy are L=I3Ω In any subsequent motion, the tip of T=I3Ω2 is restricted to move along the curve of intersection of the ellipsoids given by equations 4.6.3 and 4.6.5. That is to say, along the curve of intersection of the ellipsoids
ω21(I3I1Ω)2+ω22(I3I2Ω)2+ω23Ω2=1
and
ω21(√I3I1Ω)2+ω22(√I3I2Ω)2+ω23Ω2=1
For a specific example, I’ll suppose that the moments of inertia are in the ratio 2:3:5, and we’ll consider three cases in turn.
Case I. Rotation about the axis of least moment of inertia. That is, we’ll take I3=2, I1=3, I2=5. Since I3 is the smallest moment of inertia, each of the ratios I3I1 and I3I2 are less than 1, and √I3I1>I3I1and√I3I2>I3I2 The two ellipsoids are
ω21(0.667Ω)2+ω22(0.400Ω)2+ω23Ω2=1
and
ω21(0.816Ω)2+ω22(0.632Ω)2+ω23Ω2=1
I’ll try and sketch these:
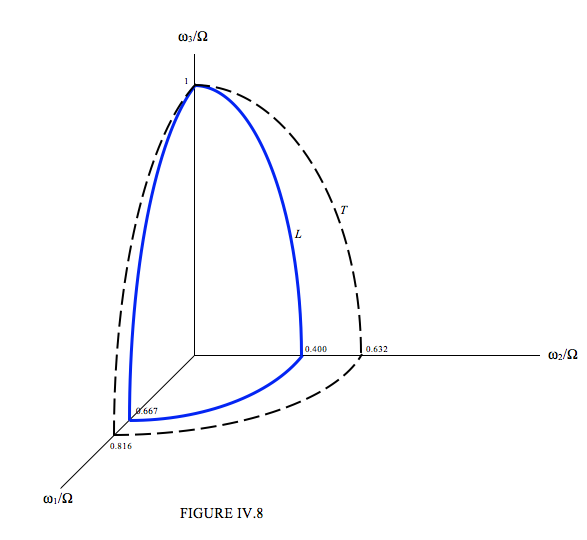
Initially, we suppose, the body was set in motion rotating about the z-axis with angular speed Ω, which determines the values of L and T, which will remain constant. The tip of the vector ω is constrained to remain on the surface of the ellipsoid L = 0 and on the ellipsoid T = 0, and hence on the intersection of these two surfaces. But these two surface touch only at one point, namely (ω1,ω2,ω3) = (0 , 0 , Ω). Thus there the vector ω remains, and the rotation is stable.
Case II. Rotation about the axis of greatest moment of inertia. That is, we’ll take I3=5, I1=2, I2=3. Since I3 is the greatest moment of inertia, each of the ratios I3I1 and I3I2 are greater than 1, and √I3I1<I3I1 and √I3I2<I3I2 The two ellipsoids are
ω21(2.50Ω)2+ω22(1.67Ω)2+ω23Ω2=1
and
ω21(1.58Ω)2+ω22(1.29Ω)2+ω23Ω2=1
I’ll try and sketch these:
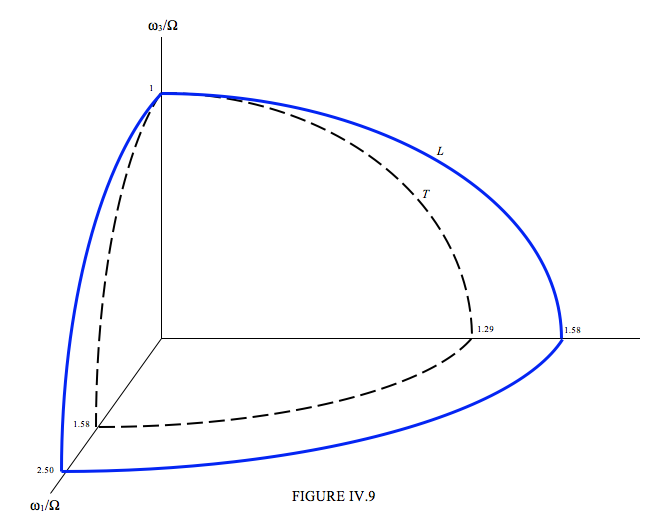
Again, and for the same reason as for Case I, we see that this motion is stable.
Case III. Rotation about the intermediate axis. That is, we’ll take I3=3, I1=5, I2=2. This time I3I1 is less than 1 and I3I2 is less than 1, and √I3I1<I3I1 and √I3I2<I3I2 The two ellipsoids are
ω21(0.60Ω)+ω22(1.50Ω)2+ω23Ω2=1
and
ω21(0.77Ω)2+ω22(1.22Ω)2+ω23Ω2=1
I'll try and sketch these:
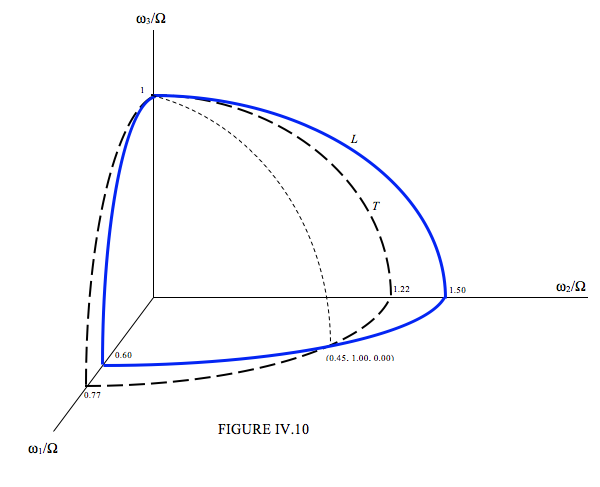
Unlike the situation for Cases I and II, in which the two ellipsoids touch at only a single point, the two ellipses for Case III intersect in the curve shown as a dotted line in figure IV.10. Thus ω is not restricted to lying along the z-axis, but it can move anywhere along the dotted line. The motion, therefore, is not stable.
You should experiment by throwing a body in the air in such a manner as to let it spin around one of its principal axes. A rectangular block will do, though the effect is particularly noticeable with something like a table-tennis bat.
Here is another approach to reach the same result. We imagine an asymmetric top spinning about one of its principal axes with angular velocity \( \boldsymbol\omega \ = \omega \hat{\bf z}). It is then given a small perturbation, so that its angular velocity is now.
ω=ϵˆx+ηˆy+ωzˆz
Here the “hatted” quantities are the unit orthogonal vectors; ϵ and η are supposed small compared with ωz. Euler’s equations are :
I1˙ϵ=ηωZ(I2−I3),
I1˙η=ωZϵ(I3−I1),
I1˙ωZ=ϵη(I1−I2).
If ϵη<<˙ωZ, then ωZ is approximately constant. Elimination of η from the first two equations yields
¨ϵ=−[(I2−I3)(I1−I3)ω2zI1I2]ϵ
Elimination of ϵ instead results in a similar equation in η.
If I3 is either the largest or the smallest of the three moments of inertia, the two parentheses in the denominator have the same sign, so the expression in the brackets is positive. Equation 4.6.22 is then the equation for simple harmonic motion, and the motion is stable. If, however, I3 is intermediate between the other two, the two parentheses have opposite sign, and the expression in brackets in negative. In that case ϵ and η increase exponentially, and the motion is unstable.
Mr Neil Honkanen of the University of Victoria conducted an experiment to illustrate the stability of rotation about the three principal axes. The body in question was a small “brick” of mild steel (density 7.83 g/cm3) of dimensions 3/8 inch × 3/4 inch × 1 1/2 inch, mass 54.1 g. In round figures, this corresponds to principal moments of inertia A0 = 2 ×10-6 kg m2, B0 = 7 × 10-6 kg m2, C0 = 8 × 10-6 kg m2. He suspended it from an electromagnet, which he set in rotation at about 25 revolutions per second, and then let it fall, while photographing it stroboscopically. He did three experiments rotation respectively about the three principle axes. You can see from the photographs below that the rotation is stable when the rotation is about the axes of greatest or least moment of inertia, but is unstable when the rotation is about the axis of intermediate moment of inertia.





