1.4: Plane Curves
- Page ID
- 6928
Plane Curves Expressed in \( x-y\) coordinates
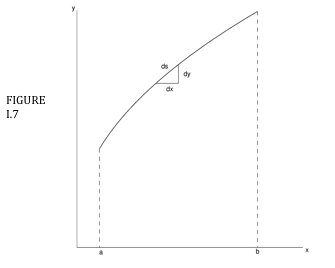
Figure I.7 shows how an elemental length \( \delta s \) is related to the corresponding increments in \( x \) and \( y \):
\[ \delta s = \sqrt{\delta x^{2} + \delta y^{2}} = \sqrt{1+\left(\dfrac{dy}{dx}\right)^{2}} \delta x = \sqrt{ \left(\dfrac{dx}{dy}\right)^{2} + 1} \, dy \label{eq:1.4.1} \]
Consider a wire of mass per unit length (linear density) \( \lambda \) bent into the shape \( y = y(x) \) between \( x = a \) and \( x=b \). The mass of an element \( ds \) is \( \lambda \delta s \), so the total mass is
\[ \int \lambda \,ds = \int_a^b \lambda \sqrt{1 + \left(\dfrac{dy}{dx}\right)^{2}} \, dx \label{eq:1.4.2} \]
The first moments of mass about the \( y \) - and \( x \) -axes are respectively
\[ \int_a^b \lambda x \sqrt{ 1+ \left(\dfrac{dy}{dx}\right)^2} \, dx \label{eq:1.4.3A} \]
and
\[ \int_a^b \lambda y \sqrt{ 1+ \left(\dfrac{dy}{dx}\right)^2} \, dx \label{eq:1.4.3B} \]
If the wire is uniform and \( \lambda \) is therefore not a function of \( x \) or \( y \), \( \lambda \) can come outside the integral signs in Equations \( \ref{eq:1.4.2}\) - \( \ref{eq:1.4.3B}\), and we hence obtain
\[ \overline{x} = \dfrac{\displaystyle \int_a^b x \sqrt{ 1+\left( \dfrac{dy}{dx} \right)^2} dx } { \displaystyle \int_a^b \sqrt{ 1+ \left(\dfrac{dy}{dx}\right)^2} dx} \label{eq:1.4.4A} \]
and
\[ \overline{y} = \dfrac{\displaystyle \int_a^b y \sqrt{ 1+\left( \dfrac{dy}{dx} \right)^2} dx } { \displaystyle \int_a^b \sqrt{ 1+ \left(\dfrac{dy}{dx}\right)^2} dx} \label{eq:1.4.4B} \]
the denominator in each of these expressions merely being the total length of the wire.
Consider a uniform wire bent into the shape of the semicircle \( x^{2} + y^{2} = a^{2} \), \( x >0 \).
First, it might be noted that one would expect \( \overline{x} > 0.4244a \) (the value for a plane semicircular lamina).
The length (i.e. the denominators in Equations \( \ref{eq:1.4.4A}\) and \( \ref{eq:1.4.4B}\)) is just \( \pi a \). Since there are, between \( x \) and \( x + \delta x \), two elemental lengths to account for, one above and one below the \( x \) axis, the numerator of Equation \( \ref{eq:1.4.4A}\) must be
\[2 \int_0^a x \sqrt{1+ \left(\dfrac{dy}{dx}\right)^{2}} dx \nonumber \]
In this case
\[y = \sqrt{a^2 - x^2} \nonumber \]
and
\[ \dfrac{dy}{dx} = \dfrac{-x}{ \sqrt{a^2 - x^2} } \nonumber \]
The first moment of length of the entire semicircle is
\[\overline{x} = 2 \int_0^a x \sqrt{ 1 + \dfrac{x^2}{a^2-x^2} } dx = 2a \int_0^a \dfrac{x\,dx}{ \sqrt{ a^2-x^2 }} \nonumber \]
From this point the student is left to his or her own devices to solve this integral and derive \( \overline{x} = \dfrac{2a}{\pi} = 0.6366a \).
Plane Curves Expressed in Polar Coordinates
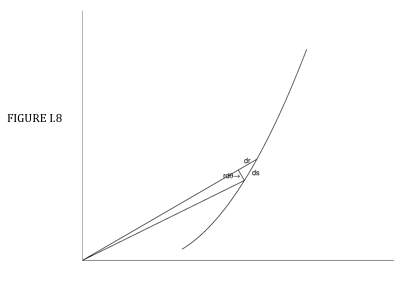
Figure I.8 shows how an elemental length \( \delta s \) is related to the corresponding increments in \( r \) and \( \theta \):
\[ \delta s = \sqrt{( \delta r)^{2} + (r \delta \theta )^{2}} = \sqrt{\left( \dfrac{dr}{d \theta }\right)^{2} + r^{2}} \, \delta \theta = \sqrt{1+\left(r \dfrac{d \theta }{dr}\right)^{2}} \,\delta r. \label{eq:1.4.5} \]
The mass of the curve (between \( \theta = a \) and \( \theta = b \) ) is
\[ \int_ \alpha ^ \beta \lambda \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} \, d \theta. \nonumber \]
The first moments about the \( y \) - and \( x \) -axes are (recalling that \( x = r \cos \theta \) and \( y = r \sin \theta \) )
\[ \int_ \alpha ^ \beta \lambda r \cos \theta \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} \, d \theta \nonumber \]
and
\[ \int_ \alpha ^ \beta \lambda r \sin \theta \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} \, d \theta. \nonumber \]
If \( \lambda \) is not a function of \( r \) or \( \theta \) , we obtain
\[ \overline{x} = \dfrac{1}{L} \int_ \alpha ^ \beta r \cos \theta \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} \, d \theta \label{eq:1.4.6A} \]
and
\[ \overline{y} = \dfrac{1}{L} \int_ \alpha ^ \beta r \sin \theta \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} d \theta \label{eq:1.4.6B} \]
where \(L\) is the length of the wire.
Again consider the uniform wire of Figure I.8 bent into the shape of a semicircle. The equation in polar coordinates is simply \( r = a \), and the integration limits are \( \theta = \dfrac{- \pi}{2} \) to \( \theta = \dfrac{+ \pi}{2} \) and the length is \( \pi a \).
Thus
\[ \overline{x} = \dfrac{1}{ \pi a} \int_{- \pi/2} ^{+ \pi/2} acos \theta [ 0 - a^{2}]^ \frac{1}{2} d \theta = \dfrac{2a}{ \pi } . \nonumber \]
The reader should now find the position of the center of mass of a wire bent into the arc of a circle of angle \( 2 \alpha \). The expression obtained should go to \( \dfrac{2 a }{\pi} \) as \( \alpha \) goes to \( \dfrac{\pi}{2} \), and to \( a \) as \( \alpha \) goes to zero.