17.3: Two Masses, Two Springs and a Brick Wall
( \newcommand{\kernel}{\mathrm{null}\,}\)
The system is illustrated in Figure XVII.2, first in its equilibrium (unstretched) position, and then at some instant when it is not in equilibrium and the springs are stretched. You can imagine that the masses are resting upon and can slide upon a smooth, horizontal table. I could also have them hanging under gravity, but this would introduce a distracting complication without illustrating any further principles. I also want to assume that all the motion is linear, so we could have them sliding on a smooth horizontal rail, or have them confined in the inside of a smooth, fixed drinking-straw. For the present, I do not want the system to bend.
The displacements from the equilibrium positions are x1 and x2, so that the two springs are stretched by x1 and x2−x1 respectively. The velocities of the two masses are ˙x1 and ˙x2. We now start the lagrangian calculation in the usual manner:
T=12m1˙x21+12m2˙x22,
V=12k1x21+12k2(x2−x1)2.
Apply Lagrange’s equation to each coordinate in turn, to obtain the following equations of motion:
m1¨x1=−(k1+k2)x1+k2x2
and
m2¨x2=k2x1−k2x2.
Now we seek solutions in which the system is vibrating in simple harmonic motion at angular frequency ω; that is, we seek solutions of the form ¨x1=−ω2x1 and ¨x2=−ω2x2.
When we substitute these in Equations ??? and ???, we obtain
(k1+k2−m1ω2)x1−k2x2=0
an\
k2x1−(k2−m2ω2)x2=0.
Either of these gives us the displacement ratio x2x1 (and hence amplitude ratio). The first gives us
x2x1=−m1ω2+k1+k2k2
and the second gives us
x2x1=k2k2−m2ω2.
These are equal, and, by equating the right hand sides, we obtain the following equation for the angular frequencies of the normal modes:
m1m2ω4−(m1k2+m2k1+m2k2)ω2+k1k2 = 0.
This equation can also be derived by noting, from the theory of equations, that Equations ??? and ??? are consistent only if the determinant of the coefficients is zero.
The meaning of these equations and of the expression “normal modes” can perhaps be best illustrated with a numerical example. Let us suppose, for example, that k1 = k2 = 1 and m1 = 3 and m2 = 2. In that case Equation ??? is 6ω4−7ω2+1=0. This is a quartic equation in ω, but it is also a quadratic equation in ω2, and there are just two positive solutions for ω. These are 1√6=0.4082 (slow, low frequency) and 1 (fast, high frequency). If you put the low frequency ω into either of Equations ??? or ??? (or in both, to check for arithmetic or algebraic mistakes) you find a displacement ratio of +1.5; but if you put the high frequency ω into either equation, you find a displacement ratio of -1.0. The first of these normal modes is a low-frequency slow oscillation in which the two masses oscillate in phase, with m2 having an amplitude 50% larger than m1. The second normal mode is a high-frequency fast oscillation in which the two masses oscillate out of phase but with equal amplitudes.
So, how does the system actually oscillate? This depends on the initial conditions. For example, if you displace the first mass by one inch to the right and the second mass by 1.5 inches to the right (this implies stretching the first spring by 1 inch and the second by 0.5 inches), and then let go, the system will oscillate in the slow, in-phase mode. But if you start by displacing the first mass by one inch to the right and the second mass by one inch to the left (this implies stretching the first spring by 1 inch and compressing the second by 2 inches), the system will oscillate in the fast, out-of-phase mode. For other initial conditions, the system will oscillate in a linear combination of the normal modes.
Thus, m1 might oscillate with an amplitude A in the slow mode, and an amplitude B in the fast mode:
x1=Acos(ω1t+α1) + Bcos(ω2t+α2) ,
in which case the oscillation of m2 is given by
x2=1.5Acos(ω1t+α1) − Bcos(ω2t+α2).
In our example, ω1 and ω2 are 1√6 and 1 respectively.
Let’s suppose that the initial conditions are that, at t = 0, ˙x1 and ˙x2 are both zero. This means that α1 and α2 are both zero or π (I’ll take them to be zero), so that
x1=Acosω1t + Bcosω2t
and
x2=1.5Acosω1t − Bcosω2t.
Suppose further that at t=0, x1 and x2 are both +1, which means that we start by stretching both springs equally. Equations ??? and ??? then become 1 = A + B and 1 = 1.5A − B. That is, A = 0.8 and B = 0.2. I’ll leave you to draw graphs of x1 and x2 versus time.
Here’s an exercise that might be useful if, perhaps, you wanted to construct a real system with two equal masses m and two equal springs, each of constant k, to demonstrate the vibrations. Show that in that case, the angular frequency (which is, of course, 2π times the actual frequency) of the slow, in phase, mode is
ω1=12(√5−1)√km = 0.6180√km
with a displacement ratio x2x1=12(√5 + 1) = 1.6180;
and the angular frequency of the fast, out of phase, mode is
ω2=12=(√5+1)√km=1.6180√km
with a displacement ratio, x2/x1=−12(√5−1)=−0.6180.
Knowing these displacements ratios will enable you to start with the appropriate initial conditions for each normal mode.
If you were to start at t = 0 with a displacements x1 = 1 and x2 = 2 which isn’t right for either normal mode, you can show that the subsequent displacements would be
x1=1.170820cosω1t−0.170820cosω2t
x2=1.894427cosω1t−0.105572cosω2t.
That looks like
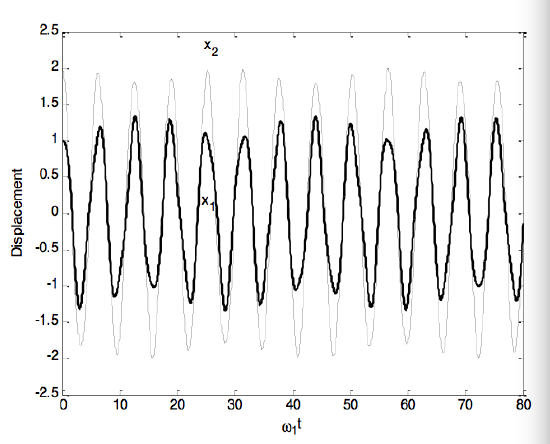
Although at first it looks like fast in-phase mode for both of them, you can see the influence of the slow mode, which has about 2.6 times the period of the last mode, in the slow amplitude modulation. If you look carefully at the modulation amplitudes of both displacements, you will see that the amplitude of the x1 displacement is out of phase with the amplitude of the x2 displacement.


