17.5: Double Pendulum
( \newcommand{\kernel}{\mathrm{null}\,}\)
This is another similar problem, though, instead of assuming Hooke’s law, we shall assume that angles are small ( sinθ≈θ,cosθ≈1−12θ2 ). For clarity of drawing, however, I have drawn large angles in Figure XVIII.4.
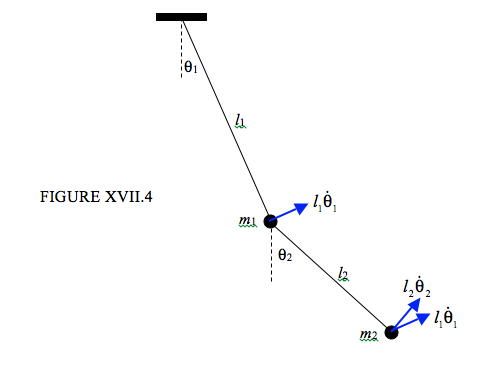
Because I am going to use the lagrangian equations of motion, I have not marked in the forces and accelerations; rather, I have marked in the velocities. I hope that the two components of the velocity of m2 that I have marked are self-explanatory; the speed of m2 is given by v22=l21˙θ21+l22˙θ22+2l1l2˙θ1˙θ2cos(θ2−θ1). The kinetic and potential energies are
T=12m1l21˙θ21+12m1[l21˙θ21+l22˙θ22+2l1l2˙θ1˙θ2cos(θ2−θ1)],
V=constant−m1gl1cosθ1−m2g(l1cosθ1+l2cosθ2).
If we now make the small angle approximation, these become
T=12m1l21˙θ21+12m2(l1˙θ1+l2˙θ2)2
and
V=contant+12m1gl1θ21+12m1g(l1θ21+l2θ22)−m1gl1−m2gl2.
Apply the lagrangian equation in turn to θ1 and θ2:
(m1+m2)l21¨θ1+m2l1l2¨θ=−(m1+m2)gl1θ1
and
m2l1l2¨θ1+m2l22¨θ2=−m2gl2θ2.
Seek solutions in the form of ˙θ1=−ωθ1 and ˙θ2=−ω2θ2.
Then
(m1+m2)(l2ω2−g)θ1+m2l1l2ω2θ2=0
and
l1ω2θ1+(l2ω2−g)θ2=0.
Either of these gives the displacement ratio θ2/θ1. Equating the two expressions for the ratio θ2/θ1, or putting the determinant of the coefficients to zero, gives the following equation for the frequencies of the normal modes:
m1l1l2ω4−(m1+m2)g(l1+l2)ω2+(m1+m2)g2=0.
As in the previous examples, there is a slow in-phase mode, and fast out-of-phase mode.
For example, suppose m1 = 0.01 kg, m2 = 0.02 kg, l1 = 0.3 m, l2 = 0.6 m, g = 9.8 m s−2.
Then 0.0018ω4−0.02446ω2=0. The slow solution is ω = 3.441 rad s−1 ( P = 1.826 s), and the fast solution is ω = 11.626 rad s−1 (P =0.540 s). If we put the first of these (the slow solution) in either of equations 17.5.7 or 8 (or both, as a check against mistakes) we obtain the displacement ratio θ2/θ1 = 1.319, which is an in-phase mode. If we put the second (the fast solution) in either equation, we obtain θ2/θ1 = −0.5689 , which is an out-of-phase mode. If you were to start withθ2/θ1 = 1.319 and let go, the pendulum would swing in the slow in-phase mode. If you were to start with θ2/θ1 = −0.5689 and let go, the pendulum would swing in the fast out-of-phase mode. Otherwise the motion would be a linear combination of the normal modes, with the fraction of each determined by the initial conditions, as in the example in Section 17.3.


