17.7: Two Masses, Three Springs, Two brick Walls

The three masses are equal, and the two outer springs are identical. Figure XVII.6 shows the equilibrium position.

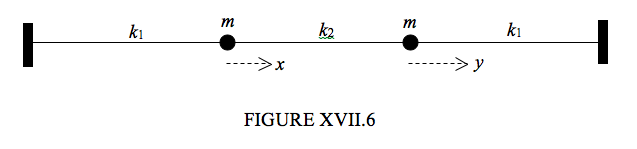
Suppose that at some instant the first mass is displaced a distance $x$ to the right and the second mass is displaced a distance $y$ to the right. The extensions of the first two springs are $x$ and $y − x$respectively, and the compression of the third spring is $y$. If the speeds of the masses are $\dot{x}$ and $\dot{y}$, we have for the kinetic and potential energies:

$$T = \frac{1}{2}m\dot{x}^2 + \frac{1}{2} m \dot{y} ^2 \label{17.7.1}$$

and

$$V = \frac{1}{2}k_1x^2 +\frac{1}{2}k_2(y - x)^2 + \frac{1}{2}k_1y^2. \label{17.7.2}$$

Apply Lagrange’s equation in turn to x and to y.

$$m \ddot{x} + (k_1 + k_2)x - k_2y = 0 \label{17.7.3}$$

and

$$m \ddot{y} + (k_1 + k_2)y - k_2x = 0. \label{17.7.4}$$

Seek solutions of the form $\ddot{x} = -\omega^2 x$ and $\ddot{y} = -\omega ^2 y$.

$$(-m \omega^2 + k_{1} + k_2) - k_2y = 0 \label{17.7.5}$$

and

$$-k_2x+(-m\omega^2 + k_1 + k_2)y = 0. \label{17.7.6}$$

On putting the determinant of the coefficients to zero, we find for the frequencies of the normal modes

$$\omega^2 = \frac{k_1}{m} \qquad \text{and} \qquad \omega^2 = \frac{k_1 + 2k_2}{m}, \label{17.7.7a, b}$$

corresponding to displacement ratios

$$\frac{x}{y} = 1 \qquad \text{and} \qquad \frac{x}{y} = -1. \label{17.7.8a,b}$$

In the first, slow, mode, the masses move in phase and there is no extension or compression of the connecting spring. In the second, fast, mode, the masses move in antiphase and the compression or extension of the coupling spring is twice the extension or compression of the outer springs.

The general motion is a linear combination of the normal modes:

$$x = A\cos(\omega_1 t+ \alpha_1) + B\cos(\omega_2 t + \alpha_2), \label{17.7.9}$$

$$y = A\cos(\omega_1 t+ \alpha_1) - B\cos(\omega_2 t + \alpha_2), \label{17.7.10}$$

$$\dot{x} = -A\sin(\omega_1 t+ \alpha_1) - B\sin(\omega_2 t + \alpha_2), \label{17.7.11}$$

$$\dot{y} = -A\sin(\omega_1 t+ \alpha_1) + B\sin(\omega_2 t + \alpha_2), \label{17.7.12}$$

Suppose that the initial condition is at $t = 0, y = \dot{y} = 0, x = x_0, \dot{x} = 0$. That is, we pull the first mass a little to the right (keeping the second mass fixed) and then we let go. The second two equations establish that $\alpha_1 = \alpha_2 = 0$, and the first two equations tell us that $A = B = x_0/2$. The displacements are then given by

$$x = \frac{1}{2} x_0(\cos \omega_1t + \cos \omega_2t) = x_0\cos\frac{1}{2}( \omega_1-\omega_2)t\cos\frac{1}{2}( \omega_1+\omega_2)t \label{17.7.13}$$

and

$$y = \frac{1}{2} x_0(\cos \omega_1t + \cos \omega_2t) = -x_0\sin\frac{1}{2}( \omega_1-\omega_2)t\sin\frac{1}{2}( \omega_1+\omega_2)t. \label{17.7.14}$$

Let us imagine, for example, that $k_2$ is much less than $k_1$ (but not negligible), so that we have two weakly-coupled oscillators. In that case equations $\ref{17.7.7a, b}$ tell us that the frequencies of the two normal modes are nearly equal. What equation $\ref{17.7.13}$ describes, then, is a rapid oscillation of the first mass with angular frequency $\frac{1}{2}(\omega_1 + \omega_2$ whose amplitude is modulated with a slow angular frequency $\frac{1}{2} (\omega_1 - \omega_2 )$. Equation $\ref{17.7.14}$ describes the same sort of motion for the second mass, except that the modulation is out of phase by 90^o with the modulation of the motion of the first mass. For a while the first mass will oscillate with a large amplitude. This will gradually decrease, while the amplitude of the motion of the second mass increases until the motion of the first mass momentarily ceases. After that, the amplitude of the motion of the second mass starts to decrease, while the first mass starts up again. And so the motion continues, with the first mass and the second mass alternately taking up the motion.