17.10: Water
( \newcommand{\kernel}{\mathrm{null}\,}\)
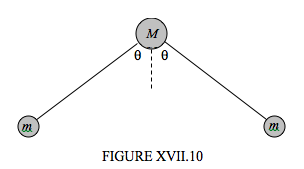
Water consists of a mass M (“oxygen”) connected to two smaller equal masses m (“hydrogen”) by two equal springs of force constants k, the angle between the springs being 2θ. The equilibrium length of each spring is r. The torque needed to increase the angle between the springs by 2δθ is 2cδθ. See Figure XVII.10. (θ is about 52°.)
At any time, let the coordinates of the three masses (from left to right) be
(x1,y1),(x2,y2),(x3,y3)
and let the equilibrium positions be
(x10,y10),(x20,y20),(x30,y30), wherey30=y10
We suppose that these coordinates are referred to a frame in which the centre of mass of the system is stationary.
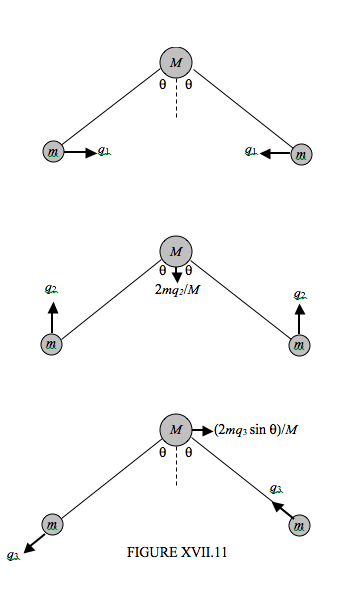
Let us try and imagine, in Figure XVII.11, the vibrational modes. We can easily imagine a mode in which the angle opens and closes symmetrically. Let is resolve this mode into an x-component and a y-component. In the x-component of this motion, one hydrogen atom moves to the right by a distance q1 while the other moves to the left by and equal distance q1. In the y-component of this symmetric motion, both hydrogens move upwards by a distance q2, while, in order to keep the centre of mass of the system unmoved, the oxygen necessarily moves down by a distance 2mq2/M. We can also imagine an asymmetric mode in which one spring expands while the other contracts. One hydrogen moves down to the left by a distance q3, while the other moves up to the left by the same distance. In the meantime, the oxygen must move to the right by a distance (2mq3sinθ)/M, in order to keep the centre of mass unmoved.
We are going to try to write down the kinetic and potential energies in terms of the internal coordinates q1,q2 and q3.
It is easy to write down the kinetic energy in terms of the (x,y) coordinates:
T = 12m(˙x21 + ˙y21) + 12M(˙x22 + ˙y22) +12m(˙x23 + ˙y23).
From geometry we have:
˙x1= ˙q1−˙q3sinθ˙y1=˙q2−˙q3cosθ˙x2=2m˙q3sinθM˙y2=−2m˙q2M˙x3=−˙q1−˙q3sinθ˙y3=˙q2 + ˙q3cosθ
On putting these into equation ??? we obtain
T = m˙q21 + m(1+2mM)˙q22 + m(1+(2msin2θ)M)˙q23
For short, I am going to write this as
T=a11˙q21+a22˙q22+a33˙q23
Now for the potential energy.
The extension of the left hand spring is
δr1=−q1sinθ−q2cosθ−2mq2cosθM+q3+2mq3sinθcosθM=−q1sinθ−q2(1+2mM)cosθ+q3(1+(2msin2θ)M)
The extension of the right hand spring is
δr2=−q1sinθ−q2cosθ−2mq2cosθM−q3−2mq3sin2θM=−q1sinθ−q2(1+2mM)cosθ−q3(1+(2msin2θ)M).
The increase in the angle between the springs is
2δθ=−2q1cosθr + 2(1+2mM)q2sinθr.
The potential energy (above the equilibrium position) is
V=12k(δr1)2 + 12k(δr2)2 + 12c(2δθ)2.
On substituting Equations ???, ??? and ??? into this, we obtain an equation of the form
V=b11q21 + 2bq12q1q2 + b22q22 + b33q23,
where I leave it to the reader, if s/he wishes, to work out the detailed expressions for the coefficients. We still have a cross term, so we can’t completely separate the coordinates, but we can easily apply Lagrange’s equation to Equations ??? and ???, and then seek simple harmonic solutions in the usual way. Setting the determinant of the coefficients to zero leads to the following equation for the angular frequencies of the normal modes:
[b11−ω2a11b120b12b22−ω2a22000b33−ω2a33] = 0.
Thus, given the masses and r,θ,k and c, one can predict the frequencies of the normal modes. Can one calculate k and c given the frequencies? I do not know, to tell the truth. Can I leave it to the reader to investigate further?


