19.4: Variations
- Page ID
- 7054
In Sections 19.1,2,3, we imagined that the cycloid was generated by a circle that was rolling counterclockwise along the line \(y = 2a\). We can also imagine variations such as the circle rolling clockwise along \(y = 0\), or we can start with P at the top of the circle rather than at the bottom. I summarise in this section four variations. The distinction between \( \psi \) and \( \theta \) is as follows. The angle that the tangent to the cycloid makes with the positively-directed \(x\)-axis is \( \psi \); that is to say, \( dx/dy = tan \psi \).The circle rolls through an angle \(2 \theta \). There is a simple relation between \( \psi \) and \( \theta \), which is different for each case.
In each figure, \(x\) and \(y\) are plotted in units of \(a\). The vertical height between vertices and cusps is \(2a\), the horizontal distance between a cusp and the next vertex is \( \pi a\), and the arc length between a cusp and the next vertex is \(4a\).
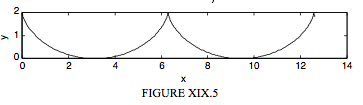
I. Circle rolls counterclockwise along \(y = 2a\). P starts at the bottom. The cusps are up. A vertex is at the origin.
\[\begin{align*} x &= a(2 \theta + \sin 2 \theta ) \\[4pt] y &= 2 a \sin^2 \theta \label{19.4.2}\tag{19.4.2} \\[4pt] s &= 4a \sin \theta \label{19.4.3}\tag{19.4.3} \\[4pt] ^2 &= 8 ay \label{19.4.4}\tag{19.4.4} \\[4pt] \psi &= \theta . \label{19.4.5}\tag{19.4.5} \end{align*} \]
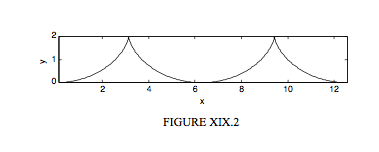
II. Circle rolls clockwise along \(y = 0\). P starts at the bottom. The cusps are down. A cusp is at the origin.
\[ x = a(2\theta - sin 2\theta ) \label{19.4.6}\tag{19.4.6} \]
\[ y = 2a sin^2 \theta \label{19.4.7}\tag{19.4.7} \]
\[ s = 4a(1-cos \theta) \label{19.4.8}\tag{19.4.8} \]
\[ s^2 = 8a(y-s) \label{19.4.9}\tag{19.4.9} \]
\[ \psi = 90 \circ - \theta. \label{19.4.10}\tag{19.4.10} \]
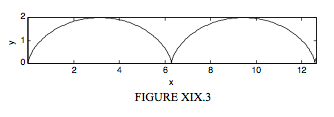
III. Circle rolls clockwise along \(y = 0\). P starts at the top. The cusps are down. A vertex is at \(x = 0\).
\[ x = a( 2 \theta + \sin 2 \theta \label{19.4.11}\tag{19.4.11} \]
\[ y = 2 a \cos^2 \theta \label{19.4.12}\tag{19.4.12} \]
\[ s = 4 a \sin \theta \label{19.4.13}\tag{19.4.13} \]
\[ s^2 = 8a(2a-y) \label{19.4.14}\tag{19.4.14} \]
\[ \psi = 180 \circ - \theta . \label{19.4.15}\tag{19.4.15} \]
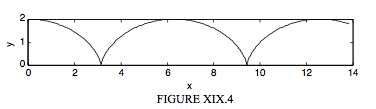
IV. Circle rolls counterclockwise along \(y = 2a\). P starts at the top. The cusps are up. A cusp is at \(x = 0\).
\[ x = a (2 \theta - \sin 2 \theta) \label{19.4.16}\tag{19.4.16} \]
\[ y = 2a \cos^2 \theta \label{19.4.17}\tag{19.4.17} \]
\[ s = 4a (1-\cos \theta) \label{19.4.18}\tag{19.4.18} \]
\[ s^2 - 8as + 8a(2a - y) = 0 \label{19.4.19}\tag{19.4.19} \]
\[ \psi = 90 \circ + \theta \label{19.4.20}\tag{19.4.20} \]