19.5: Motion on a Cycloid, Cusps Up

We shall imagine either a particle sliding down the inside of a smooth cycloidal bowl, or a bead sliding down a smooth cycloidal wire, Figure XIX.6.

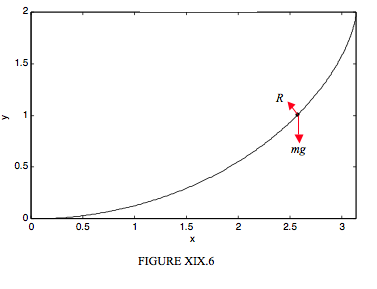
We shall work in intrinsic coordinates to obtain the tangential and normal Equations of motion. These Equations are, respectively:

$$\ddot{s} = -g \sin \psi \label{19.5.1}\tag{19.5.1}$$

and

$$\dfrac{mv^2}{ \rho} = R - mg \cos \psi. \label{19.5.2}\tag{19.5.2}$$

Here R is the normal (and only) reaction of the bowl or wire on the particle and $\rho$ is the radius of curvature. The radius of curvature is $ds/d \psi$, which, from Equation 19.3.1, (or Equations 19.4.3 and 19.4.5) is

$$\rho = 4 a \cos \psi \label{19.5.3}\tag{19.5.3}$$

From Equations 19.3.1 and $\ref{19.5.1}$ we see that the tangential Equation of motion can be written, without approximation:

$$\ddot{s} = -\dfrac{g}{4a}s. \label{19.5.4}\tag{19.5.4}$$

This is simple harmonic motion of period $4 \pi \sqrt{a/g}$, independent of the amplitude of the motion. This is the isochronous property of the cycloid. Likewise, if the particle is released from rest, it will reach the bottom of the cycloid in a time $\pi \sqrt{a/g}$ whatever the starting position.

Let us see if we can find the value of R where the generating angle is $\psi$. Let us suppose that the particle is released from rest at a height $y_0$ above the $x$-axis (generating angle = $\psi_0$ ); what is its speed $v$ when it has reached a height $y$ (generating angle $\psi$ )? Clearly this is given by

$$\dfrac{1}{2} mv^2 = mg(y_0 - y), \label{19.5.5}\tag{19.5.5}$$

and, following Equation 19.3.2, and recalling that $\theta = \psi$, this is

$$v^2 = 2ga(cos2 \psi - cos2 \psi_0 ). \label{19.5.6}\tag{19.5.6}$$

On substituting this and Equation $\ref{19.5.3}$ into Equation $\ref{19.5.2}$, we find for R:

$$R = \frac{mg}{2 \cos \psi }(1+ 2 \cos 2 \psi - \cos 2 \psi_0) \label{19.5.7}\tag{19.5.7}$$