22.8: Appendix B
( \newcommand{\kernel}{\mathrm{null}\,}\)
Solutions to Miscellaneous Problems
By proportions, hk=nx and hl=mx and therefore hk+hl=1.
Therefore by Pythagoras:
h(1√a2−x2+1√b2−x2)=1..
Everything but x is known in this equation, which can therefore be solved for x. There are several ways of solving it; here’s a suggestion. If we put in the numbers, the equation becomes
3(1√64−x2+1√100−x2)−1=0.
Put X=100−x2, and the equation becomes
3(1√X−36+1√X)−1=0.
This can be written f(X)=3(A+B)−1=0, where A and B are obvious functions of X. Differentiation with respect to X gives f′(X)=−32(A3+B3) and Newton-Raphson iteration (X=X−ff′) soon gives X, from which it is then found that x= 6.326 182 m.
In the corotating frame the bob is in equilibrium under the action of three forces – its weight, the tension in the string and the centrifugal force. (If you do not like rotating reference frames and centrifugal force, it will be easy for you to do it “properly”.) Resolve the forces perpendicular to the string: ml0sinαΩ2.cosα = mgsinα and the problem is finished.
Raising or lowering the board does not apply any torques to the system, so the angular momentum L is conserved. That is,
L=ml2sin2θ.ωis constant.
We also have that
g = lcosθ.ω.
i. Eliminate w from these equations. This gives:
l3sin3θtanθ=L2gm2
which is constant.
ii. Eliminate l from equations (1) and (2). This gives:
ω3cot2θ=mg2L,
which is constant.
iii. Eliminate θ from equations (1) and (2). This gives:
ω3(ωl2−Lm)=g2.
(Check the dimensions of all the equations.) Then we can get Lm from equation (1) and hence
ω3(ωl2−Ωl20sin2α)=g2,
which is constant.
l3sin3θtanθ=l30sin3αtanα=0.023675 m3.
Although we are asked to plot θ vertically versus l horizontally, it is easier, when working out numerical values, to calculate l as a function of θ. That is,
l = 0.287142sinθ3√tanθ.
(The number in the numerator is the cube root of 0.023675.)
For l = 40 cm = 0.4 m, the semivertical angle is given by
sin3θtanθ=0.369 923.
The solution to this is
θ=45∘ 31′.
(See Section 1.4 of Celestial Mechanics if you need to know how to solve the equation f(x)=0.)
ω3cot2θ=Ω3cot2α
With the given data, this is ω3=199.385tan2θ.
iii. ω3(ωl2−Ωl20sin2α)= Ω3(Ωl20 − Ωl20sin2α)=Ω4l20cos2α.
That is, ω3(ωl2 −a)= g2 where, with the given initial data,
a=0.48168 m2s−1 and g2 = 96.04 m2s−4.
Although we are asked to plot ω vertically versus l horizontally, it is easier, when working out numerical values, to calculate l as a function of ω. That is,
l2 = g2ω4+aω.
To solve the above equation for ω might be slightly easier with the substitution of u for 1ω:
g2u4 + au −l2=0.
With l = 0.6 m, this gives u= 0.226121 rad-1 s, and hence ω = 4.422 rad s-1. As in part (b) i, it is necessary to know how to solve the equation f(x)=0. See Section 1.4 of Celestial Mechanics if you need to know how.
There are no horizontal forces, because the table is smooth. Therefore the centre of mass of the rod falls vertically.centre of mass of the rod falls vertically.
From energy considerations
12m˙y2 + 12(13ml2)˙θ2 + mgy =constant.
But y = lcosθ and therefore ˙y=−lsinθ.˙θ.
(3sin2θ + 1)l˙θ2 + 6gsinθ=C.
Initially θ=˙θ=0,∴C=6g.
˙θ2 = 6g(1−cosθ)l(3sin2θ+1)__
Also, since ˙y2=l2sin2θ˙θ2 and ˙x2=l2cos2θ˙θ2, we obtain
˙y2 = 6glsin2θ(1−cosθ)3sin2θ+1__
and
˙x2 = 6glcos2θ(1−cosθ)3sin2θ+1__
Of course ˙θ and ˙y increase monotonically with θ; but ˙x starts and finishes at zero, and must go through a maximum. With c = cosθ, Equation (5) can be written
˙x2 = 6glc(1−c)4−3c2,
and by differentiating ˙x2 with respect to c, we see that ˙x2 is greatest at an angle θ given by
3c2 −12c+8=0,
the solution of which is θ = 37∘ 50′__.
If the length of the rod is 1 m (l = 0.5 m) and ˙x = 1 m s-1, Equation 4 becomes
26.4c2 −29.4c + 4 = 0,
and the two solutions are θ = 17∘ 15′__ and 80∘ 52′__.
The reader who has done all the problems so far will be aware of the importance of being able instantly to solve the equation f(x)=0. If you have not already done so, you should write a computer or calculator program that enables you to do this instantly and at a moment’s notice. See Section 1.4 of Celestial Mechanics if you need to know how.
If you want to find the normal reaction N of the table on the lower end of the rod, you could maybe start with the vertical equation of motion m¨y=N−mg. Differentiate Equation (4): 2˙y¨y= whatever, and the use equation
4 again for ˙y. This looks like rather heavy and uninteresting algebra to me, so I shan’t pursue it. There may be a better way...
In the figure below I have marked in red the forces on the rod, namely its weight mg and the horizontal and vertical components X and Y of the reaction of the hinge on the rod. I have also marked, in green, the transverse and radial components of the acceleration of the centre of mass. The transverse component is l¨θ and the radial component is the centripetal acceleration l˙θ2.centre of mass. The transverse component is l¨θ and the radial component is the centripetal acceleration l˙θ2.
From consideration of the moment of the force mg about the lower end of the rod, it is evident that the angular acceleration is
¨θ=3gsinθ4l
and by writing ¨θ as ˙θd˙θdθ and integrating (with initial conditions θ = ˙θ = 0), or from energy considerations, we obtain the angular speed:
˙θ2=3g(1−cosθ)2l.
The horizontal and vertical equations of motion are:
X=ml(¨θcosθ−˙θ2sinθ)
and
mg − Y = ml(¨θsinθ + ˙θ2cosθ).
(As ever, check the dimensions - and count the dots!)
After substitution for ¨θ and ˙θ2 we find
X = 34mgsinθ(3sinθ−2)
and
Y = 14mg(1−3cosθ)2.
The results follow immediately.
Call the length of the rod 2l. Initially the height above the table of its centre of mass is lcos40°, and its gravitational potential energy is mg l cos40∘. When it hits the table at angular speed w, its kinetic energy is 12Iω2 = 12(43ml2)ω2 = 23ml2ω2. Therefore,
ω = √3gcos40∘2l = 4.746 rad s−1 =271.9 deg s−1__.
To find the time taken, you can use Equation 9.2.10:
t = √I2∫90∘40∘dθ√E−V(θ).
Here, I = 34ml2, E=mglcos40∘, V(θ) = mglcosθ and therefore
t = √2l3g∫9040dθ√cos40∘−cosθ.
The magnitude of the quantity before the integral sign is 0.184428 s. To find the value of the integral requires either that you be an expert in elliptic integrals or (more likely and more useful) that you know how to integrate numerically (see Celestial Mechanics 1.2.) I make the value of the integral 2.187314, so that the time taken is 0.4034 seconds. When integrating, note that the value of the integrand is infinite at the lower limit. How to deal with this difficulty is dealt with in Celestial Mechanics 1.2. It cannot be glossed over.
Here is the diagram. The forces are the weight mg of the rod, and the force of the table on the rod. However, I have resolved the latter into two components – the normal reaction N of the table on the rod, and the frictional force F, which may be either to the left or the right, depending on whether rod is tending to slip towards the right or the left. The magnitude of F is less than μN as long as the rod is not jus about the slip. When the rod is just about to slip, F=μN, μ being the coefficient of limiting static friction.
Just as in Problem 5, the equations of motion, as long as the rod does not slip, are
F = 34mgsinθ(3cosθ−2)
and
N = 14mg(1−3cosθ)2.
FN=3sinθ(3cosθ−2)(1−3cosθ)2.
The figure below shows FN as a function of θ. One sees that, as the rod falls over, FN increases, and, as soon as it attains a value of μ, the rod will slip. We see, however, that FN reaches a maximum value, and by calculus we can determine that it reaches a maximum value of 15√10128 = 0.3706 when θ = θ−1(911)=35∘06′. If μ < 0.3706, the bottom of the rod will slip before θ=35∘06′. If, however, μ > 0.3706, the rod will not have slipped by the time θ=35∘06′, and it is safe for a while as FN starts to decrease. When θ reaches cos−1(23)=48∘11′, the frictional force changes sign and thereafter acts to the left. (The frictional force of the table on the rod acts to the left; the frictional force of the rod on the table acts to the right.) We know by now (since the rod survived slipping before θ=35∘06′ that the magnitude of FN can be at least as large
as 0.3706, and it does not reach this until θ=51∘15′. Therefore, if the rod hasn’t slipped by θ=51∘15′ it won’t slip before θ=51∘15′. But after that it is in danger again of slipping. FN becomes infinite (N=0) when θ=cos−1(13)=70∘32′, so it will certainly slip (to the right) before then.
If μ=0.25, the rod will slip to the left when
3sinθ(3cosθ−2)(1−3cosθ)2 = 14, or θ=19∘39′__.
If μ=0.75, the rod will slip to the right when
3sinθ(3cosθ−2)(1−3cosθ)2 = −34, or θ=53∘07′__.
Again, it is very necessary that you prepare for yourself a program that will instantly solve the equation f(x)=0.
Let the length of the ladder be 2l. By geometry, the distance OC remains equal to l throughout the motion; therefore C describes a circle of radius l, centre O. I have marked in, in green, the radial and transverse components of the acceleration of C, namely l˙θ2 and l¨θ. The angular speed of the ladder is ˙θ and the linear speed of the centre of mass C is l¨θ. I have also marked, in red, the three forces acting on the ladder, namely its weight and the reactions of the floor and the wall on the ladder.centre O. I have marked in, in green, the radial and transverse components of the acceleration of C, namely l˙θ2 and l¨θ. The angular speed of the ladder is ˙θ and the linear speed of the centre of mass C is l¨θ. I have also marked, in red, the three forces acting on the ladder, namely its weight and the reactions of the floor and the wall on the ladder.
The angular speed ˙θ can be obtained from energy considerations. That is, the loss of potential energy in going from angle a to the vertical to angle θ is equal to the gain in translational and rotational kinetic energies:
mgl(cosα−cosθ)=12m(l˙θ)2 + 12(12ml2)˙θ2.
˙θ2=3g2l(cosα−cosθ).
The angular acceleration ¨θ can be obtained from the following equation:
mglsinθ=43ml2¨θ
The derivation of Equation (2) raises some points of interest, and I discuss it in an Appendix at the end of the problem.
The vertical and horizontal equations of motion are:
N2 = m(l¨θcosθ−l˙θ2sinθ)
and
mg − N1 =m(l¨θsinθ + l˙θcosθ),
although we need only the first of these, because we wish to find out when N2 = 0.
On substitution for ¨θ and ˙θ2 we find that
N2 = 34mgsinθ(3cosθ−2cosα)
and
N1 = 14mg(1−6cosαcosθ+9cos2θ)
We need only the first of these to see that N2 becomes zero (and hence the upper end loses contact with the wall) when cosθ=23cosα.
Appendix: Derivation of equation (2).
In my original posting of this solution I had derived Equation (2) by considering that the total moment of all forces about Q is mglsinθ, and the rotational inertia with respect to Q is 43ml2. I then equated mglsinθ to 43ml2¨θ. I am indebted to correspondent Amin Rezaee Zadeh for pointing out a flaw in this argument, and for supplying a correct derivation. The flaw is that I am applying the equation τ=˙L to a moving point Q. In Section 3.12 of Chapter 3 of these notes it is pointed out that τ=˙L can be applied to a moving point only if the moving point satisfies one or more of three conditions, and it is evident in this problem that Q satisfies none of these conditions. I present Mr Rezaee’s correct derivation of Equation (2 ) below.
I shall be making use of Equations ??? and ???:
˙LQ = τQ + Mr′q × ¨rQ.
LQ = Σ(ri−rQ)×[mi(vi−vQ)].
I shall also be making use of the notation used in Section 3.12, and I reproduce here Figure III.7 from that Section, and I also draw the relevant vectors appropriate to this ladder problem.
In the figure below, I have indicated an elemental portion ds of the ladder at a distance s from the upper end of the ladder. Its mass is evidently dm=mds2l. I have drawn the position vectors ri and rO of ds and of Q. This notation corresponds to the same notation used in Section 3.12. From the geometry of the figure, we can determine that
ri = ssinθi + (2l−s)cosθj
and
rQ = 2lsinθi + 2lcosθj,
where i and j are the unit vectors in the x− and y− directions respectively.
On differentiation with respect to time, we find the following expressions for the velocities of the element ds and the point Q, in which I again retain the notation used in Section 3.12:
vi = s˙θcosθi − (2l−s)˙θsinθj
and
vQ = 2l˙θcosθi − 2l˙θsinθj
On making use of Equation 3.12.2, we obtain for the angular momentum of the element ds with respect to Q:
dLQ = m2l(ri−rQ)×[(vi−vQ)]ds.
The instantaneous angular momentum of the entire ladder about Q is therefore
LQ = m2l∫2l0(ri−rQ)×[(vi−vQ)]ds.
On substitution of Equations (A1) – (A4) into equation (A6) and a modest amount of algebra, we obtain
LQ = mθk2l∫2l0s(s−2l)ds = −23ml2˙θk,
where k is the unit vector in the z−direction. (The z−direction is out of the plane of the “paper”, and therefore LQ is into the plane of the “paper”. It is worth spending a moment or two trying to imagine this. The ladder is rotating counterclockwise about C, while C and Q are moving in clockwise trajectories. It may not be immediately obvious to decide whether one would expect LQ to be directed into or out of the plane of the “paper”. Equation (A7) answers this question.)
We now make use of Equation 3.12.1:
˙LQ = τQ + mr′QרrQ.
Let us find expressions for the four vector quantities in this equation.
By differentiation of Equation (A7) with respect to time, we obtain
˙LQ = −23ml2¨θk.
The torque about Q is
τQ = mglsinθk
We can see from the geometry of the figure (see especially the second of our figures, in which we see that r′Q and ¯r are the same in magnitude and direction) that
r′Q = lsinθi + lcosθj.
Finally, by differentiation of Equation (A4) (in which ), we obtain
¨rQ = 2l[(¨θcosθ−˙θ2sinθ)i − (¨θsinθ−˙θ2cosθ)j].
Substitution of Equations (A9) to (A12) into Equation (A8) gives, after some algebra,
mglsinθ = 43ml2¨θ.
This is Equation (2), quod erat demonstrandum.
It will, I think, be agreed that the point O remains fixed in space as long as the semicylinder remains in contact with wall and floor. Therefore the centre of mass C moves in a circle around O. We’ll call the radius of the circle, which is the distance between O and C, b, which, for a semicylinder, equals centre of mass C moves in a circle around O. We’ll call the radius of the circle, which is the distance between O and C, b, which, for a semicylinder, equals 4a(3π) (see Chapter 1), where a is the radius of the semicylinder. I have marked, in red, the three forces on the semicylinder, and also, in green, the radial and transverse components of the acceleration.
The angular speed ˙θ can be obtained from energy considerations. The gain in kinetic energy in going from rest to an angular speed ˙θ is 12(mk2)˙θ2 and the gain in potential energy when the centre of mass drops through a vertical distance b sinθ is mgbsinθ. Here k is the radius of gyration about O, which, for a semicylinder, is given by k2=12a2.
[I have left b and k as they are in the equations, so that the analysis could easily be adapted, if needed, for a hollow semicylinder, or a solid hemisphere, or a hollow hemisphere. From Chapters 1 and 2 we recall:
| Solid semicylinder: | b=4a3π | k2 = 12a | b2k2 = 329π2 |
| Hollow semicylinder: | b=2aπ | k2 = a2 | b2k2 = 4π2 |
| Solid hemisphere: | b=3a8 | k2 = 25a2 | b2k2 = 45128 |
| Hollow hemisphere: | b=12a |
k2 = 23a2 |
b2k2 = 38 |
On equating the gain in kinetic energy to the loss in potential energy, we obtain
˙θ2 = 2bgk2sinθ.
The angular acceleration ¨θ can be obtained from applying τ = I¨θ about O:
mgbcosθ = mk2¨θ,
from which
¨θ = bgk2cosθ
The horizontal and vertical equations of motion are
N2 = mb(˙θ2cosθ +¨θsinθ)
and
N2 = mb(˙θ2cosθ +¨θsinθ)
We do not really need Equation (4), because we are trying to determine when N2=0.
On substitution from Equations (1) and (2), Equation (3) becomes
N1=6mb2ga2sinθcosθ.
This is zero when θ = 0∘ (which was the initial condition) or when θ = 0∘, at which point contact with the wall is lost, which it was required to show.
At this instant, the rotational velocity is √2bgk2 counterclockwise.
and the linear velocity of C is b√2bgk2 horizontally to the right.
The rotational kinetic energy is 12Iω2 where ω = √2bgk2, and I is the rotational inertia about the centre of masscentre of mass, which is m(k2−b2).
Krot=mbg(k2−b2)k2.
The translational kinetic energy is 12mv2 where v = √2bgk2.
Ktr = mb3gk2
The sum of these is mbg, which is just equal to the loss of the original potential energy, which serves as a check on the correctness of our algebra.
There are now no horizontal forces, so the horizontal component of the velocity of C remains constant. The semicylinder continues to rotate, however, until the rotational kinetic energy is converted to potential energy and C rises to its maximum height. If the base then makes an angle ϕ with the vertical, the gain in potential energy is mbgsinϕ, and equating this to the rotational kinetic energy gives
sinϕ = 1 − b2k2.
This gives the following results:
| Solid semicylinder: | ϕ = 39∘ 46′ |
| Hollow semicylinder: | ϕ = 36∘ 30′ |
| Solid hemisphere: | ϕ = 40∘ 25′ |
| Hollow hemisphere: | ϕ = 38∘ 41′ |
Add text here. For the automatic number to work, you need to add the "AutoNum" template (preferably at the end) to the page.
It is well known that if α > tan−1μ the particle will slide down the plane unless helped by an extra force. I have drawn the three forces acting on the particle. Its weight mg. The reaction R of the plane on the particle; if the particle is in limiting static equilibrium, this reaction will make an angle λ (“the angle of friction”) with the plane such that tanλ = μ. It therefore makes an angle α−θ with the vertical. Finally, the additional force P needed; we do not initially know the direction of this force.
When three (or more) coplanar forces are in equilibrium and are drawn head-to-tail, they form a closed triangle (polygon). I draw the triangle of forces below.
It will be clear from the triangle that P is least when the angle between P and R is 90∘:
The least value of P is therefore mg(sinαcosλ − cosαsinλ). But tanλ=μ and therefore sinλ=μ√1+μ2 and cosλ=1√1+μ2.
Pmin=mg(sinα−μcosα)√1−μ2
and P then makes an angle \( \lambda\) with the plane.
You may, if you wish, go further, and show that when P makes an angle β with the plane, it must have magnitude
P=sinα−μcosαμsinβ + cosβmg.
You can then differentiate this with respect to β (you need only differentiate the denominator) and show that this is a minimum when \beta\ =\ \lambda. That is just a harder way of finding what we already found by using the triangle of forces.
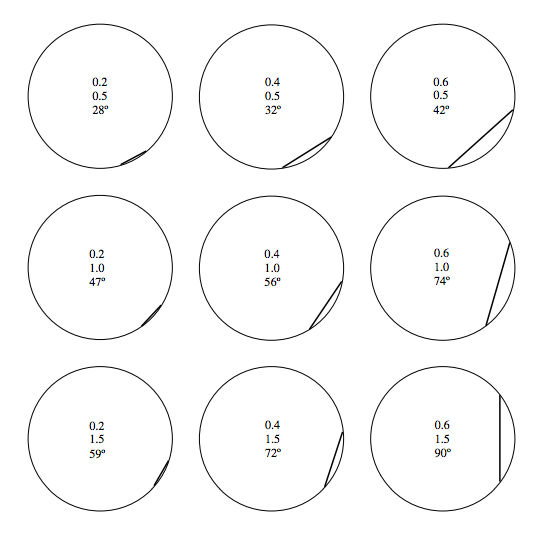
For \alpha\ =\ 70^{\circ} and \mu\ =\ 0.8, P varies with \beta like this:
This goes through a minimum of P_{\text{min}}=0.520m\text{g} at \beta\ =\ \tan^{-1}0.8=38^{\circ}.7.
_________________________
Add text here. For the automatic number to work, you need to add the "AutoNum" template (preferably at the end) to the page.
As the cylinder rolls down the plane, the wedge, because its base is smooth, will slide towards the left. Since there are no external horizontal forces on the system, the centre of mass of the system will not move horizontally (or, rather, it won’t accelerate horizontally.)centre of mass of the system will not move horizontally (or, rather, it won’t accelerate horizontally.)
As usual, we draw a large diagram, using a ruler , and we mark in the forces in red and the accelerations in green, after which we’ll apply F\ =\ ma to the cylinder, or to the wedge, or to the system as a whole, in two directions. It should be easy and straightforward.
I have drawn the linear acceleration \ddot{s} of the cylinder down the slope, and its angular acceleration \ddot{\theta}. I have drawn the linear acceleration \ddot{x} of the wedge, which is also shared with the cylinder. I have drawn the gravitational force mg on the cylinder. There is one more force on the cylinder, namely the reaction of the wedge on the cylinder. But I’m not sure in which direction to draw it. Is it normal to the plane? That would mean there is no frictional force between the cylinder and the plane. Is that correct (remembering that both the cylinder and the wedge are accelerating)? Of course I could calculate the moment of the force mg about the point of contact of the cylinder with the plane, and then I wouldn’t need to concern myself with any forces at that point of contact.
But then that point of contact is not fixed. Oh, dear, I’m getting rather muddled and unsure of myself.
This problem, in fact, is ideally suited to a lagrangian rather than a newtonian treatment, and that is what we shall do. Lagrange proudly asserted that it was not necessary to draw any diagrams in mechanics, because it could all be done analytically. We are not quite so talented as Lagrange, however, so we still need a large diagram drawn with a ruler. But, instead of marking in the forces and accelerations in red and green, we mark in the velocities in blue.
No frictional or other nonconservative forces do any work, so we can use Lagrange’s equations of motion for a conservative holonomic system; \frac{d}{dt}\left(\frac{\partial T}{\partial \dot{q}}\right)-\left(\frac{\partial T}{\partial q}\right)=-\left(\frac{\partial V}{\partial q}\right).
The speed of the wedge is \dot{x} and the speed of the centre of mass of the cylinder is centre of mass of the cylinder is \sqrt{\dot{s}^{2}+\dot{x}^{2}-2\dot{s}\dot{x}\cos\alpha} and the angular speed of the cylinder is \frac{\dot{s}}{a}.
The kinetic energy of the system is
T\ =\ \frac{1}{2}m(\dot{s}^{2}+\dot{x}^{2}-2\dot{s}\dot{x}\cos\alpha)\ +\ \frac{1}{2}(mk^{2})\left(\frac{\dot{s}}{a}\right)\ +\ \frac{1}{2}M\dot{x}^{2},
or
T\ =\ \frac{1}{2}m\left(1+\frac{k^{2}}{a^{2}}\right)\dot{s}^{2}\ -\ m\dot{s}\dot{x}\cos\alpha\ +\ \frac{1}{2}(m\ +\ M)\dot{x}^{2},
and the potential energy is
V\ =\ \text{constant}\ -\ m\text{g}s\sin\alpha
Application of Lagrange’s equation to the coordinate x gives us
\left(1+\frac{k^{2}}{a^{2}}\right)\ddot{s}=\ddot{x}\cos\alpha\ +\ \text{g}\sin\alpha.
and application of Lagrange’s equation to the coordinate s gives us
m\ddot{s}\cos\alpha\ =\ (m+M)\ddot{x}
Elimination of \ddot{s} from these two equations gives us
\ddot{x}=\frac{m\text{g}\sin\alpha\cos\alpha}{(m+M)\left(1+\frac{k^{2}}{a^{2}}\right)-m\cos^{2}\alpha}
You can also easily find an expression for \ddot{s} is you wish.
There is no acceleration normal to the plane, and therefore N\ =\ m\text{g}\cos\alpha. The frictional force F acts along the tangent to the path and is equal to \mu N, or \mu m\text{g}\cos\alpha, where \mu is the coefficient of moving friction. We are told to ignore the difference between the coefficients of moving and limiting static friction. Since the particle was originally at rest in limiting static friction, we must have \mu\ =\ \tan\alpha. Therefore F\ =\ m\text{g}\sin\alpha. The tangential equation of motion is
m\ddot{s}\ =\ -F\ + whatever the component of m\textbf{g} is in the tangential direction in the sloping plane.
The component of m\textbf{g} down the plane would be (look at the left hand drawing) m\text{g}\sin\alpha, and so its tangential component (look at the right hand drawing) is m\text{g}\sin\alpha\sin\psi. So we have, for the tangential equation of motion,
m\ddot{s}=-m\text{g}\sin\alpha\ +\ m\text{g}\sin\alpha\sin\psi,
or
\ddot{s}=-\text{g}\sin\alpha(1-\sin\psi).
We are seeking a relation between V and \psi, so, in the now familiar fashion, we write V\frac{dV}{ds} for \ddot{s}, so the tangential equation of motion is
V\frac{dV}{ds}=-\text{g}\sin\alpha(1-\sin\psi). \tag{1}\label{12.1}
We also need the equation of motion normal to the trajectory. The component of m\textbf{g} in that direction is m\text{g}\sin\alpha\cos\psi, and so the normal equation of motion is
\frac{mV^{2}}{\rho}\ =\ m\text{g}\sin\alpha\cos\psi.
Here \rho is the radius of curvature of the path, which is the reciprocal of the curvature \frac{ds}{d\psi}. The normal equation of motion is therefore
V^{2}\frac{d\psi}{ds}\ =\ \text{g}\sin\alpha\cos\psi. \tag{2}\label{12.2}
Divide Equation ( \ref{1}) by Equation ( \ref{2}) to eliminate s and thus get a desired differential equation between V and \psi:
\frac{1}{V}\frac{dV}{d\psi}\ =\ -\frac{(1-\sin\psi)}{\cos\psi}. \tag{3}\label{12.3}
This is easily integrated; a convenient (not the only) way is to multiply top and bottom by 1\ +\ \sin\psi. In any case we soon arrive at
\ln V\ =\ -\ln(1+\sin\psi)\ +\ \text{constant}, \tag{4}\label{12.4}
and with the initial condition V\ =\ V_{0} when \psi\ =\ 0, this becomes
\underline{\underline{V=\frac{V_{0}}{1+\sin\psi}}}. \tag{5}\label{12.5}
In the limit, as \psi\rightarrow90^{\circ},\ V\rightarrow\frac{1}{2}V_{0}. The particle is then moving at constant velocity and is in equilibrium under the forces acting upon it just when it was initially at rest.
13.
M_{1} = mass of complete sphere of radius a.
M_{1} = mass of missing inner sphere of radius xa.
M = mass of given hollow sphere.
We have M\ =\ M_{2}-M_{1} and \frac{M_{2}}{M_{1}}=x^{3} and therefore
M_{1}\ =\ \frac{M}{1-x^{3}} and M_{2}\ =\ \frac{Mx^{3}}{1-x^{3}}.
Also I=\frac{2}{5}M_{1}a^{2}\ -\ \frac{2}{5}M_{2}x^{2}a^{2}\ =\ \frac{2}{5}a^{2}(M_{1}-M_{2}x^{2}).
Hence I=\frac{2}{5}Ma^{2}\times\frac{1-x^{5}}{1-x^{3}}.
If x=0,\ I\ =\ \frac{2}{5}Ma^{2}, as expected. If x\rightarrow1, you may have to use de l’Hôpital’s rule to show that I\rightarrow\frac{2}{5}Ma^ {2} as expected.
M_{1} = mass of mantle.
M_{2} = mass of core.
M = mass of entire planet.
We have M=M_{1}+M_{2} and \frac{M_{1}}{M_{2}}=\frac{s(1-x^{3})}{x^{3}} and therefore
M_{2}\ =\ M\times\frac{x^{3}}{x^{3}\ +\ s(1-x^{3})} and M_{1}\ =\ M\times\frac{s(1-x^{3})}{x^{3}\ +\ s(1-x^{3})}
Also
I\ =\ I_{\text{core}}\ +\ I_{\text{mantle}}\ =\ \frac{2}{5}M_{2}x^{2}a^{2}\ +\ \frac{2}{5}M_{1}a^{2}\times\frac{1-x^{5}}{1-x^{3}},
where I have made use of the result from the previous problem. On substitution of the expressions for M_{1} and M_{2}, we quickly obtain
I\ =\ \frac{2}{5}Ma^{2}\times\frac{s\ +\ (1-s)x^{5}}{s\ +\ (1-s)x^{3}} \tag{1}\label{14.1}
A hollow planet would correspond to \frac{1}{s}=0. Divide top and bottom by s and it is immediately seen that the expression for a hollow planet would be identical to the expression obtained for the previous problem.
Note that both x\ =\ 0 and x\ =\ 1 correspond to a uniform sphere, so that in either case, I\ =\ \frac{2}{5}Ma^{2} for all other cases, the moment of inertia is less than \frac{2}{5}Ma^{2}.
The core size for minimum moment of inertia is easily found by differentiation of the above expression for I, and the required expression follows after some algebra. For s\ =\ 0.6, the equation becomes 9-15x^{2}-4x^{5}\ =\ 0, of which the only positive real root is x\ =\ 0.73682, which corresponds to a moment of inertia of 0.90376 % \frac{2}{5}Ma^{2}. Note that. for s\ =\ 0.6, the moment of inertia, expressed in units of \frac{2}{5}Ma^{2} varies very little as the core size goes from 0 to 1, so that measurement of the moment of inertia places very little restriction on the possible core size.
The inverse of Equation ( \ref{1}) is
(1-s)x^{5}\ -\ I(1-s)x^{3}\ +\ (1-I)s\ =\ 0, \tag{2}\label{14.2}
where I is expressed in units of \frac{2}{5}Ma^{2}. For I\ =\ 0.911, there are two positive real roots (look at the graph); they are x\ =\ 0.64753 and 0.81523. For I\ =\ 0.929, the roots are 0.55589 and 0.87863. Thus the core size could be anything between 0.55589 and 0.64753 or between 0.81523 and 0.87863 a rather large range of uncertainty. Even if I were known exactly (which does not happen in science), there would be two solutions for x.
This is just a matter of geometry. If, when you make a small angular displacement, you raise the centre of mass of the brick the equilibrium is stable. For, while the brick is in its vertical position, it is evidently at a potential minimum, and you have to do work to raise the centre of mass. If, on the other hand, your action in making a small angular displacement results in a lowering of the centre of mass, the equilibrium is unstable.centre of mass of the brick the equilibrium is stable. For, while the brick is in its vertical position, it is evidently at a potential minimum, and you have to do work to raise the centre of mass. If, on the other hand, your action in making a small angular displacement results in a lowering of the centre of mass, the equilibrium is unstable.
When the brick is in its vertical position, the height h_{0} of its centre of mass above the base of the semicylinder is justcentre of mass above the base of the semicylinder is just
h_{0}\ =\ R\ +\ l.
When it is displaced from the vertical by an angle \theta, the point of contact between brick and semicylinder is displaced by a distance R\theta, and, by inspection of the drawing, the new height h is
h\ =\ R\cos\theta\ +\ R\theta\sin\theta\ +l\cos\theta.
h-h_{0}\ =\ R\theta\sin\theta\ -\ (R+l)(1-\cos\theta).
If you Maclaurin expand this as far as \theta^{2}, you arrive at
h-h_{0}\approx\frac{1}{2}(R-l)\theta^{2}.
This is positive, and therefore the equilibrium is stable, if l\ <\ R, or 2l\ <\ 2R, i.e. if the length of the brick is less than the diameter of the semicylinder.
As in the previous question, it is just a matter of geometry. If rolling the Thing results in raising its centre of mass, the equilibrium is stable. Initially, the height of the centre of mass is H_{0}\ =\ b\ + l.centre of mass, the equilibrium is stable. Initially, the height of the centre of mass is H_{0}\ =\ b\ + l.
After rolling, the dashed line, which joins the centres and is of length a+b, makes an angle \theta with the vertical. The short line joining the centre of mass of the Thing to the centre of curvature of its bottom is of length l-a and it makes an angle \theta+\\phi with the vertical. The height of the centre of mass is therefore nowcentre of mass of the Thing to the centre of curvature of its bottom is of length l-a and it makes an angle \theta+\\phi with the vertical. The height of the centre of mass is therefore now
h\ =\ (a+b)\cos\theta+(l-a)\cos(\theta+\phi)
The centre of mass has therefore rise through a heightcentre of mass has therefore rise through a height
h\ -\ h_{0}\ = (a+b)\cos\theta\ +\ (l-a)\cos(\theta+\phi)\ -b-l.
Also, the two angles are related by a\phi\ =\ b\theta, so that
h\ -\ h_{0}\ = (a+b)\cos\theta\ +\ (l-a)\cos\left[\left\{1+\left(\frac{b}{a}\right)\right\}\theta\right]\ -b-l
h\ -\ h_{0}\ = -\frac{1}{2}\theta^{2}[a+b\ +\ (l-a)(1+\frac{b}{a})^{2}].
For stability this must be positive, and hence \frac{1}{l}\ >\ \frac{1}{a}\ +\ \frac{1}{b}.
If a\ =\ b, this becomes l\ <\ \frac{1}{2}a.
| For a hollow semicylinder, | l\ =\ (1-\frac{2}{\pi})a=0.363a | \Box Stable |
| For a hollow hemisphere, | l=0.5a | \Box Borderline stable |
| For a solid semicylinder, | l\ =\ [1-\frac{4}{(3\pi)}]a=0.576a | \Box Unstable |
| For a solid hemisphere, | l=\frac{5}{8}a=0.625a | \Box Unstable |
We need to find the height h of the centre of mass above the level of the pegs as a function of \theta. See drawing on next page.centre of mass above the level of the pegs as a function of \theta. See drawing on next page.
Angels:
\text{BAC}\ =\ 45^{\circ}-\theta
\text{ABX}\ =\ 45^{\circ}+\theta
Distances:
\text{AB}\ =\ 2ka
\text{AC}\ =\ 2ka\ \cos(45^{\circ}-\theta)
\text{EF}\ =\ 2ka\ \cos(45^{\circ} -\theta)\cos(45^{\circ}+\theta)=ak\cos2\theta
\text{DC}\ =\ a\sqrt{2}
\text{DF}\ =\ a\sqrt{2}\cos\theta
h\ =\ \text{DF}\ -\ \text{EF}\ =\ a(\sqrt{2}\cos\theta-k\cos2\theta)
h_{0}= height of centre of mass above pegs when \theta = 0 centre of mass above pegs when \theta\ =\ 0^{\circ}\ =\ a(\sqrt{2}-k)
y\ =\ \frac{h}{h_{0}}\ =\frac{\sqrt{2}\cos\theta-k\cos2\theta}{\sqrt{2}-k}
There are three forces acting on the hemisphere: Its weight m\text{g}. The reaction N of the wall, which is perpendicular to the wall since the wall is smooth. The reaction R of the floor, which acts at an angle \lambda to the floor, where \mu\ =\ \tan\lambda. Three forces in equilibrium must act through a point; therefore all three forces act through the point P. It is thus clear that
\sin\ \theta\ =\ \frac{\text{OP}}{\text{OC}}\ =\ \frac{a\mu}{\frac{3}{8}a}\ =\ \frac{8\mu}{3}.
If \mu\ =\ \frac{1}{4},\ \theta\ =\ 41^{\circ}48'. If \mu\ =\ \frac{3}{8},\ \theta\ =\ 90^{\circ}. If \mu\ >\ \frac{3}{8} the hemisphere can rest in any position, the equilibrium not being limiting static equilibrium.
This solution uses the same method that Professor Marsh (Warwick University) showed me for Problem 20. I believe it to be clearer than an earlier solution that I had posted.
At an instant when the rod is tilted at angle \theta, the coordinates of C with respect to the fixed point O are:
\overline{x}\ =\ a(\sin\theta\ -\ \theta\cos\theta), \tag{1}\label{19.1}
\overline{y}\ =\ a(\cos\theta\ +\ \theta\sin\theta) \tag{2}\label{19.2}
and so its velocity components are
\dot{\overline{x}}\ =\ a\theta\sin\theta\dot{\theta} \tag{3}\label{19.3}
and
\dot{\overline{y}}\ =\ a\theta\cos\theta\dot{\theta}. \tag{4}\label{19.4}
The moment of inertia of the rod about the centre of mass is \frac{1}{3}ml^{2}.
The kinetic energy T is the sum of the translational kinetic energy and the rotational kinetic energy about the centre of mass:centre of mass:
T\ =\ \left(\frac{1}{2}a^{2}\theta^{2}\ +\ \frac{1}{6}l^{2}\right)m\dot{\theta}^{2}, \tag{5}\label{19.5}
and the potential energy V is
V\ =\ m\text{g}a(\cos\ \theta\ +\ \theta\sin\ \theta). \tag{6}\label{19.6}
One can now get the equation of motion either by Lagrangian means or by equating the derivative with respect to \theta of the total energy to zero, since there are no nonconservative forces and hence the total energy is independent of \theta. In carrying out the differentiation, note that \frac{d}{d\theta}\dot{\theta}^{2}\ =\ 2\dot{\theta}\frac{d\dot{\theta}}{d\theta}\ =\ 2\ddot{\theta}. We obtain, for the equation of motion:
a^{2}\theta\dot{\theta}^{2}\ +\ (a^{2}\theta^{2}+\frac{2}{3}l^{2})\ddot{\theta}\ +\ \text{g}a\theta\cos\theta\ =\ 0 \tag{7}\label{19.7}
For small \theta (neglecting second and higher powers of \theta), \cos\theta\rightarrow 1 and a^{2}\theta^{2} is negligible compared with l^{2}, so the equation of motion becomes, approximately, \ddot{\theta}=-\frac{3\text{g}a}{l^{2}}, and so the period is \underline{\underline{P\ =\ \frac{2\pi l}{\sqrt{3\text{g}a}}}}.
I am much indebted to Professor T. R. Marsh of Warwick University not only for finding a mistake in an earlier posted solution to this problem, but for providing the following solution.
I\ =\ ma^{2}\left(\frac{7}{5}\ -\ \frac{3}{4}\cos\theta\right). \tag{2}\label{20.2b}
x\ =\ \frac{3a\theta}{8}
We are going to refer the motion to a fixed point Q, which is the point of contact between hemisphere and table when the hemisphere is in its equilibrium position.
At an instant when the hemisphere is tilted at an angle \theta, the distance between A and Q is a\theta, and the coordinates of C relative to Q are
\overline{x}\ =\ a\theta\ -\ \frac{3}{8}a\sin\theta, \tag{1}\label{20.1}
\overline{y}\ =\ a -\ \frac{3}{8}a\cos\theta. \tag{2}\label{20.2}
Therefore the velocity components of C are
\dot{\overline{x}}\ =\ a\left(1-\frac{3}{8}\cos\theta\right)\dot{\theta}, \tag{3}\label{20.3}
\dot{\overline{y}}\ =\ \frac{3}{8}a\sin\theta\dot{\theta}. \tag{4}\label{20.4}
By the parallel axes theorem, the moment of inertia around the centre of mass iscentre of mass is
I\ =\ \frac{2}{5}ma^{2}\ -\ m\left(\frac{3}{8}a\right)^{2}\ =\ \frac{83}{320}ma^{2} \tag{5}\label{20.5}
The kinetic energy T is the sum of the translational kinetic energy and the rotational kinetic energy about the centre of mass:centre of mass:
T\ =\ \frac{1}{2}ma^{2}\left[\left(1-\frac{3}{8}\cos\theta\right)^{2}\ +\ \left(\frac{3}{8}\sin\theta\right)^{2}\ +\ \frac{83}{230}\right]\dot{\theta}^{2}\ =\ ma^{2}\left(\frac{7}{10}-\frac{3}{8}\cos\theta\right)\dot{\theta}^{2} \tag{6}\label{20.6}
The potential energy V is
V\ =\ m\text{g}a(1-\frac{3}{8}\cos\theta). \tag{7}\label{20.7}
We can the get the equation of motion either by using the Lagrangian equations, or by calculating the derivative with respect to \theta of the total energy T\ +\ V. The derivative is zero, because there are no nonconservative forces and total energy is constant. Note that (as in Problem 19) the derivative of \dot{\theta}^{2} with respect to \theta is 2\dot{\theta}\frac{d\dot{\theta}}{d\theta}, which is 2\ddot{\theta}. Either method results in the equation of motion:
\left(\frac{7}{5}\ -\ \frac{3}{4}\cos\theta\right)\ddot{\theta}\ + \frac{3}{8}\sin\theta\dot{\theta}^{2}\ + \frac{3}{8}\text{g}\sin\theta\ = 0. \tag{8}\label{20.8}
In the small angle limit, \cos\theta\rightarrow 1, and \sin\theta\rightarrow \theta is negligible compared with \text{g}, so the equation of motion becomes
\ddot{\theta}\ =\ -\frac{15\text{g}}{26a}\theta \tag{9}\label{20.9}
\underline{\underline{P\ =\ 2\pi\sqrt{\frac{26a}{15\text{g}}}}}. \tag{10}\label{20.10}
The (second) moment of inertia with respect to the centre (see centre (see Section 2.19 of Chapter 2) is
I_{\text{centre}} = 4 \pi \rho_0 \int^a_0 (r^4-r^5/a)dr = \frac{2}{15}\pi\rho_0a^5..
The moment of inertia with respect to an axis through the centre is 2/3 of this:centre is 2/3 of this:
I_{\text{axis}}\ =\ \frac{4}{45}\pi\rho_{0}a^{5}.
\therefore \qquad \qquad \qquad \underline{\underline{I_{\text{axis}}\ =\ \frac{4}{15}Ma^{2}}}.
Left-hand particle: T\ =\ m\text{g}[\mu\cos(\alpha-\theta)\ +\ \sin(\alpha-\theta)].
Right-hand particle: T\ =\ m\text{g}[\sin(\alpha+\theta)\ -\ \mu\cos(\alpha+\theta)].
\therefore \qquad \mu[\cos(\alpha-\theta)\ +\ \cos(\alpha+\theta)]\ =\ \sin(\alpha+\theta)\ -\ \sin(\alpha-\theta),
and, by the “sum and difference” trigonometrical formulae, we obtain
2\mu\cos\alpha\cos\theta\ =\ 2\cos\alpha\sin\theta,
from which
\underline{\underline{\tan\ \theta\ =\ \mu.}}
Consider a portion of the rope between \theta and \delta\theta. There are four forces on this portion. The tension T at \theta. The tension T\ +\ \delta T at \theta\ +\ \delta\theta ( \delta T is negative). The normal reaction \delta N of the cylinder on the rope. The frictional force \mu\delta N of the cylinder on the rope. Note that the rope is about to slip downwards, so the friction force is upwards as shown.
We have
\delta N\ =\ (2T\ +\ \delta T)\sin\left(\frac{1}{2}\theta\right)
and
(T\ +\ \delta T)\cos\left(\frac{1}{2}\delta\theta\right)\ +\ \mu\delta N\ =\ T\cos\left(\frac{1}{2}\delta\theta\right).
To first order, these become
\delta N\ =\ T\delta\theta
\delta T\ =\ -\mu\delta N
and
\delta T\ =\ -\mu T\delta\theta
and hence by integration
\underline{\underline{F\ =\ M\text{g}e^{-\mu\alpha}}}.
Area of square = 4a^{2}
Area of rectangle = 4a^{2}(1-x)
Area of triangle = 2a^{2}(x+y-1)
Area of trapezoid = 2a^{2}(1-x+y)
The weight of the cube is 8a^{3}\rho s\text{g}, and it acts downward through C, the centre of mass. The hydrostatic upthrust is 4a^{3}(1-x+y)\rho\text{g} and it acts upward through the centre of buoyancy H. Here \rho is the density of the fluid, and \rho s is the density of the wood. We evidently must find the centre of mass. The hydrostatic upthrust is 4a^{3}(1-x+y)\rho\text{g} and it acts upward through the centre of buoyancy H. Here \rho is the density of the fluid, and \rho s is the density of the wood. We evidently must find the X'- coordinate of C and of H. Let’s first of all find the X- and Y- coordinates (see the next figure).
The X- and Y-coordinates of C are trivial and quite easy respectively:
X_{C}\ =\ a \qquad \qquad Y_{C}\ =\ a(1-2x)
You are going to have to work quite hard at it to find the X- and Y- coordinates of H, the centre of buoyancy, which is the centroid of the trapezoid. “After some algebra” you should findcentre of buoyancy, which is the centroid of the trapezoid. “After some algebra” you should find
X_{H}\ =\ \frac{2(1-x+2y)a}{3(1-x+y)} \qquad \qquad Y_{H}\ =\ \frac{2(2-4x+2y+2x^{2}-2xy-y^{2})a}{3(1-x+y)}
To find the X'- coordinates of C and of H, we use the usual formulas for rotation of axes, being sure to get it the right way round:
\begin{pmatrix}X'\\Y'\end{pmatrix}\ =\ \begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{pmatrix}\begin{pmatrix}X\\Y\end{pmatrix},
together with
\tan\ \theta\ =\ x\ +\ y-1.
Take moments about the axle (origin):
8a^{3}\rho s\text{g}X'_{C}\ =\ 4a^{3}\rho\text{g}(1-x+y).
After a little more algebra, you should eventually arrive at
\underline{\underline{s=\frac{3-7x+2y+6x^{2}-3y^{2}-2x^{3}+y^{3}+3xy^{2}}{3(2-3x-y+2x^{2}+2xy)}}}
Let the radii of the cylinder and sphere be a and b respectively, and the mass of the sphere be M. The angles \theta and \phi are related by a\theta\ =\ b\phi. I have drawn the three forces on the sphere, namely its weight, the normal reaction of the cylinder on the sphere, and the frictional force on the sphere. The transverse acceleration of the centre of the sphere is (a+b)\ddot{\theta} and the centripetal acceleration is (a+b)\dot{\theta}^{2}. The equations of motion are:centre of the sphere is (a+b)\ddot{\theta} and the centripetal acceleration is (a+b)\dot{\theta}^{2}. The equations of motion are:
M\text{g}\sin\theta\ -\ F\ =\ M(a+b)\ddot{\theta} \tag{1}\label{25.1}
and
M\text{g}\cos\theta\ -\ N\ =\ M(a+b)\dot{\theta}^{2} \tag{2}\label{25.2}
The angular acceleration of the sphere about its centre is \ddot{\theta}\ +\ \ddot{\phi}\ =\ \left(1+\frac{a}{b}\right)\ddot{\theta}, and its rotational inertia is \frac{2Mb^{2}}{5}. The torque that is causing this angular acceleration is Fb, and therefore the rotational equation of motion is
Fb =\ \frac{2}{5}Mb^{2}\left(1+\frac{a}{b}\right)\ddot{\theta} \tag{3}\label{25.3}
Elimination of F between Equations ( \ref{20.1}) and ( \ref{20.3}) yields
\ddot{\theta} = \frac{5\text{g}}{7(a+b)}\sin\theta. \tag{4}\label{20.4}
Write \ddot{\theta} as \dot{\theta}\frac{d\dot{\theta}}{d\theta} in the usual way and integrate with initial conditions \theta=\dot{\theta}=0 or from energy considerations:
\dot{\theta}^{2} =\frac{10\text{g}}{7(a+b)}(1-\cos\theta) \tag{5}\label{20.5}
Substitute for \ddot{\theta} and \dot{\theta}^{2} into Equation ( \ref{20.2}) to obtain
N =\ M\text{g}(17\cos\theta-10). \tag{6}\label{20.6}
This is zero, and the sphere leaves the cylinder, when \cos\theta\ =\ \frac{10}{17}, \theta\ =\ 53^{\circ}58'.
Surface density = \sigma g cm-2
Original sandwich:
Mass = 54 \sigma g
x-coordinate of centre of mass = 3 cm centre of mass = 3 cm
y-coordinate of centre of mass = 4 cm centre of mass = 4 cm
Bite:
Mass = \frac{1}{2}\pi3^{2}\sigma =14.137 166 94 \sigma g
Distance of centre of mass from hypotenuse = centre of mass from hypotenuse= \frac{4}{3\pi}\times 3\ =\ \frac{4}{\pi} = 1.273 239 545 cm
x-coordinate of centre of mass = 4.5 -centre of mass = 4.5\ -\ \frac{4}{\pi}\sin\theta=4.5-\frac{16}{5\pi} = 3.481 408 364 cm
y-coordinate of centre of mass = 6- centre of mass = 6\ -\ \frac{4}{\pi}\cos\theta\ =\ 6-\frac{12}{5\pi} = 5.236 056 273 cm
Remainder:
Mass = (54 - 14.137 166 94) \sigma = 39.862 833 06 \sigma g
x-coordinate of centre of mass = \overline{x}centre of mass = \overline{x}![]()
y-coordinate of centre of mass = \overline{y}centre of mass = \overline{y}![]()
Moments:
39.862 833 06 \overline{x} + 14.137 166 94 × 3.481 408 364 = 54 × 3. \underline{\underline{\overline{x} = 2.829\ 270\ 780\ \text{cm}}}
39.862 833 06 \overline{y} + 14.137 166 94 × 5.236 056 273 = 53 × 4. \underline{\underline{\overline{y}\ =\ 3.561\ 638\ 436\ \text{cm}}}
This point is very close to the edge of the bite. The centre of the bite is at (4.5, 6), and its radius is 3. Its equation is thereforecentre of the bite is at (4.5, 6), and its radius is 3. Its equation is therefore
(x-4.5)^{2}\ +\ (y-6)^{2}\ =9, or x^{2}\ +\ y^{2}\ -9x\ -12y\ +\ 47.25=0.
The line x = 2.829 270 780 cuts the circle where y^{2}-12y\ +\ 29.791\ 336\ 13\ =\ 0. The lower of the two points of intersection is at y = 3.508 280 941 cm. The centre of mass is slightly higher than this and is therefore just inside the bite.centre of mass is slightly higher than this and is therefore just inside the bite.
Consider a portion of the band within the angle \delta\theta. Its mass is \frac{m\delta\theta}{2\pi} When the band is spinning at angular speed \omega and its radius is r, the centrifugal force on that portion is \delta F\ =\ \frac{mr\omega^{2}\delta\theta}{2\pi}. (I leave it to the philosophers and the schoolteachers to debate as to whether there “really” is “such thing” as centrifugal force – I want to get this problem done, and I’m referring to a co-rotating frame.) The y-component of this force is \frac{mr\omega^{2}\delta\theta}{2\pi}. Also, the tension in the band when its radius is r is T=2\pi k(r-a).
Consider the equilibrium of half of the band. The y-component of the centrifugal force on it is \frac{mr\omega^{2}}{2\pi}\int_{-\frac{\pi}{2}}^{+\frac{\pi}{2}}\cos\theta d\theta=\frac{mr\omega^{2}}{\pi}. The opposing force is 2T\ =\ 4\pi k(r-a). Equating these gives \underline{\underline{\omega^{2}\ =\ \frac{4\pi^{2}k(r-a)}{mr}}}.
Let the distance AB be l and the distance AC be c. Let the mass of the rod be m.
Consider an elemental portion \delta x of the rod at P at a distance x from A. Its weight is \frac{m\delta x}{l}. When the rod is about to move, it will experience a frictional force \delta f\ =\ \frac{\mu m\text{g}\delta x}{l}, which will be in the direction shown if P is to the left of C, and in the opposite direction if P is to the right of C. When the rod is just about to move (but has not yet done so) it is still in equilibrium. Consider the moment about A of the frictional forces on the rod. The clockwise moment of the frictional forces on AC must equal the counterclockwise moment of the frictional forces on CB. Thus
\frac{\mu m\text{g}}{l}\int_{0}^{c}x\ dx=\frac{\mu m\text{g}}{l}\int_{c}^{l}x\ dx.
\therefore \qquad\qquad \underline{\underline{c=\frac{l}{\sqrt{2}}}}.
The net force on the rod is
F\ -\ \frac{\mu m\text{g}}{l}\int_{0}^{c}dx\ +\ \frac{\mu m\text{g}}{l}\int_{c}^{l} dx,
and this is zero, and therefore
\underline{\underline{F\ =\ \frac{\mu m\text{g}(2c-l)}{l}=(\sqrt{2}-1)\mu m\text{g}.}}
The cone slips when \tan\theta\ >\ \mu.
It tips when C (the centre of mass) is to the left of M. centre of mass) is to the left of M.
The distance OC is \frac{h}{4}. (See Chapter 1, Section 1.7). Therefore it tips when \tan\theta>4\frac{a}{h}.
Thus it slips if \mu<4\frac{a}{h} and it tips if \mu<4\frac{a}{h}.
When the block is just about to tip, the reaction of the table on the block acts at A and it is directed towards the point K, because, when three coplanar forces are in equilibrium they must act through a single point. The angle \lambda is given by \tan\lambda\ =\ \frac{a}{x}. However, by the usual laws of friction, the block will slip as soon as \tan\lambda\ =\ \mu. Thus the block will slip if \mu<\frac{a}{x}, and it will tip if \mu>\frac{a}{x}. Expressed otherwise, it will slip if x<\frac{a}{\mu} and it will tip if x>\frac{a}{\mu}. The greatest possible value of x is 2a; therefore the block will inevitably slip if \mu < \frac{1}{2}
+
When or if the cylinder is just about to tip, it is about to lose contact with the left hand peg. The only forces on the cylinder are the torque, the weight, and the reaction R of the right hand peg on the cylinder, which must be vertical and equal to m\text{g}. But the greatest possible angle that the reaction R can make with the surface of the cylinder is the angle of friction \lambda given by \tan\ \lambda\ =\ \mu. From geometry, we see that \sin\ \theta\ =\ k, or \tan\ \theta\ =\ \frac{k}{\sqrt{1-k^{2}}}. Thus the cylinder will slip before it tips if \mu\ <\ \frac{k}{\sqrt{1-k^{2}}} and it will tip before it slips if \mu\ >\ \frac{k}{\sqrt{1-k^{2}}}.
If the cylinder tips (which it will do if \mu\ >\ \frac{k}{\sqrt{1-k^{2}}}), the clockwise torque t at that moment will equal the counterclockwise torque of the couple ( R and m\text{g}), which is m\text{g}ka. Thus the torque when the cylinder tips is
TIP:
\tau\ =\ m\text{g}ak. \tag{1}\label{31.1}
When or if the cylinder is just about to slip, the forces are as shown above, in which I have resolved the reactions of the pegs on the cylinder into a normal reaction (towards the axis of the cylinder) and a frictional force, which, when slipping is about to occur, is equal to m times the normal reaction. The equilibrium conditions are
\mu(N_{1}\ +\ N_{2})\cos\theta\ +\ (N_{1}-N_{2})\sin\theta\ =\ 0,
\mu(N_{1}\ -\ N_{2})\sin\theta\ -\ (N_{1}+N_{2})\cos\theta\ +\ m\text{g}=\ 0
and
\mu(N_{1}\ +\ N_{2})a\ =\ \tau.
We can find N_{1}\ +\ N_{2} by eliminating N_{1}\ -\ N_{2} from the first two equations, and then, writing \sqrt{1-k^{2}} for \cos\theta, we find that, when slipping is about to occur,
SLIP:
\tau\ =\ m\text{g}a\ \times\ \frac{\mu}{1+\mu^{2}}\ \times\ \frac{1}{\sqrt{1-k^{2}}}. \tag{2}\label{31.2}
I have drawn below the functions
\frac{\tau}{m\text{g}a}\ =\ k\ \text{(tip) and}\ \frac{\tau}{m\text{g}a}\ =\ \frac{\mu}{1\ +\ \mu^{2}}\times\frac{1}{\sqrt{1-k^{2}}}\ \text{(slip)}
for k\ =\ 0.1,\ 0.3,\ 0.5,\ \frac{1}{\sqrt{2}} and 0.9. The horizontal lines are the tip functions, and the curves are the slip functions. As long as \mu\ <\ \frac{k}{\sqrt{1-k^{2}}} the cylinder will slip. As soon as \mu\ <\ \frac{k}{\sqrt{1-k^{2}}} the cylinder will tip.
We’ll leave to the philosophers the question as to whether centrifugal force “really exists”, and we’ll work in a co-rotating reference frame, so that the car, when referred to that frame, is in static equilibrium under the six forces shown. Clearly, N_{1} and N_{2}\ =\ m\text{g} and F_{1}\ +\ F_{2}\ =\ \frac{mv^{2}}{R}.
The car slips when F_{1}\ +\ F_{2}\ =\ \mu(N_{1}+N_{2}); that is, when v\ =\ \sqrt{\mu\text{g}R}.
The car tips when \frac{mv^{2}h}{R}\ =\ m\text{g}d; that is, when v\ =\ \sqrt{\frac{d\text{g}R}{h}}.
That is, it will slip or tip according as to whether \mu\ < \frac{d}{h} or > \frac{d}{h}.
For example suppose d\ =\ 60\ \text{cm},\ h\ =\ 60\ \text{cm},\ \text{g}\ =\ 9.8\ \text{m s}^{-2},\ R\ =\ 30\ \text{m},\ \mu\ =\ 0.8.
In that case, \frac{d}{h}\ =\ 0.75, so it will tip at v\ =\ 14.8\ \text{m s}^{-1}\ =\ 53.5\ \text{km hr}^{-1}.
But if it rains, reducing \mu to 0.7, it will slip at v\ =\ 14.3\ \text{m s}^{-1}\ =\ 51.6\ \text{km hr}^{-1}.
I have drawn in green the radial and transverse components of the acceleration of the centre of mass a\dot{\theta}^{2} and a\ddot{\theta} respectively. I have drawn in red the weight of the rod and the normal and frictional components of the force of the table on the rod at A, N and F respectively.centre of mass a\dot{\theta}^{2} and a\ddot{\theta} respectively. I have drawn in red the weight of the rod and the normal and frictional components of the force of the table on the rod at A, N and F respectively.
The following are the equations of motion:
Normal:
ma\ddot{\theta}\ =\ m\text{g}\cos\theta\ -\ N. \tag{1}\label{33.1}
Lengthwise:
ma\dot{\theta}^{2}\ =\ -m\text{g}\sin\theta\ +\ F. \tag{2}\label{33.2}
Rotation:
k^{2}\ddot{\theta}\ =\ \text{g}a\cos\theta \tag{3}\label{33.3}
Here k is the radius of gyration about A, given by
k^{2}\ =\ \frac{1}{3}l^{2}\ +\ a^{2}. \tag{4}\label{33.4}
From Equations ( \ref{33.1}), ( \ref{33.3}) and ( \ref{33.4}), we obtain
N\ =\ m\text{g}\cos\theta.\left(\frac{l^{2}}{l^{2}\ +\ 3a^{2}}\right). \tag{5}\label{33.5}
The space integral (see Chapter 6, Section 6.2) of Equation ( \ref{33.3}), with initial condition \dot{\theta}\ =\ 0 when \theta\ =\ 0, results in
\dot{\theta}^{2}\ =\ \frac{2\text{g}a}{k^{2}}\sin\theta. \tag{6}\label{33.6}
This can also be obtained by equation the loss of potential energy, m\text{g}a\sin\theta to the gain in kinetic energy, \frac{1}{2}mk^{2}\dot{\theta}^{2}.
Combining this with Equations ( \ref{33.2}) and ( \ref{33.4}) leads to
F\ =\ m\text{g}\sin\theta.\left(\frac{l^{2}\ +\ 9a^{2}}{l^{2}\ +\ 3a^{2}}\right). \tag{7}\label{33.7}
At the instant of slipping, F\ =\ \mu N, and hence, from Equations ( \ref{33.5}) and ( \ref{33.7}) we find
\tan\theta\ =\ \frac{\mu}{1\ +\ 9(\frac{a}{l})^{2}}.
I derive v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2} by two different methods – one from energy considerations, the other from angular momentum considerations. First, energy.
If the table top is taken to be the zero level for potential energy, the initial potential energy was -\frac{1}{2}m.\text{g}.\frac{1}{4}l\ =\ -\frac{1}{8}m\text{g}l.
When the length of the dangling portion is \frac{1}{2}l\ +\ x the potential energy is
-\left(\frac{\frac{1}{2}l\ +\ x}{l}\right)m.\text{g}.\frac{1}{2}\left(\frac{1}{2}l\ +\ x\right)\ =\ -\frac{m\text{g}}{2l}\left(\frac{1}{2}l\ +\ x\right)^{2}\ =\ -\frac{1}{8}m\text{g}l\ -\ \frac{1}{2}m\text{g}l\ -\ \frac{m\text{g}x^{2}}{2l}.
The loss of potential energy is therefore \frac{1}{2}m\text{g}x\ +\ \frac{m\text{g}x^{2}}{2l}.
This is equal to the gain in kinetic energy \frac{1}{2}mv^{2}, and therefore
v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2}.
Another method:
Consider a point A. Anywhere will do, but I have chosen it to be a distance l below the level of the table and l to the left of the table edge. The moment of momentum (= angular momentum) of the chain about this point is mlv\ =\ ml\dot{x} and its rate of change is therefore mlv\ =\ ml\dot{x}. The torque about A is \left(\mlv\ =\ ml\dot{x} and its rate of change is therefore mlv\ =ml\dot{x}. The torque about A is \left(\frac{\frac{1}{2}l\ +\ x}{l}\right)m\text{g}l\ =\ \left(\frac{1}{2}l\ +\ x\right)m\text{g}. These are equal, and so l\ddot{x}\ =\ \text{g}\left(\frac{1}{2}l\ +\ x\right). Write \ddot{x}\ =\ v\frac{dv}{dx} in the usual way, and integrate (with v=0 when x=0) and the result v^{2}\ =\ \text{g}x\ +\ \frac{g}{l}x^{2} follows.
To find the relation between x and t we can use the energy Equation 9.2.9 for conservative systems
t\ =\ \sqrt{\frac{m}{2}}\int_{x_{0}}^{x}\frac{dx}{\sqrt{E-V(x)}}.
Here x_{0}\ =\ 0 and we have already seen that E\ -\ V(x)\ =\ \frac{m\text{g}}{2l}x^{2}\ +\ \frac{m\text{g}x}{2}. Upon integrating this expression, we obtain, after a little algebra and calculus,
\tag{1}\label{34.1}
The converse of this is the required expression
\tag{2}\label{34.2}
Differentiation of this with respect to time produces the third required expression:
\tag{3}\label{34.3}
You may verify from these last two equations, if you wish, that v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2}.
The chain falls completely off the table when x\ =\ \frac{1}{2}l. That is (by using Equation ( \ref{34.1})), at time \sqrt{\frac{l}{g}}\ln(2\ +\ \sqrt{3})\ =\ 1.317\sqrt{\frac{l}{\text{g}}}.
If we express distances in units of l, time in units of \sqrt{\frac{l}{\text{g}}} and therefore necessarily speeds in units of \sqrt{\text{g}l}, Equations ( \ref{34.2}) and ( \ref{34.3}) become
x\ =\ \frac{(e^{t}-1)^{2}}{4e^{t}}\ =\ \frac{1}{4}(e^{t}\ +\ e^{-t}-2)\ =\ \frac{1}{2}(\cosh t-1) \tag{4}\label{34.4}
v\ =\ \frac{e^{2t}-1}{4e^{t}}\ =\ \frac{1}{2}\sinh\ t \tag{5}\label{34.5}
and we can get the acceleration by a further differentiation:
a\ =\ \frac{1}{4}(e^{t}\ +\ e^{-t})\ =\ \frac{1}{2}\cosh\ t. \tag{6}\label{34.6}
We are pleased to note that, by the time that x\ =\ \frac{1}{2}l [i.e. when the chain completely leaves the table at time t\ =\ \ln(2\ +\ \sqrt{3})\sqrt{\frac{l}{\text{g}}} ], the acceleration is \text{g}. The speed is then \sqrt{\frac{3}{4}l\text{g}}\ =\ 0.866\sqrt{l\text{g}}.
The maximum overhang of book \bf{1} is d_{1}\ =\ w.
The centre mass of \bf{1\ +\ 2}centre mass of \bf{1\ +\ 2} is at \frac{3w}{2} from the left hand side (LHS) of \bf{2}, so d3\ =\ \frac{w}{3}.
The distance of the centre of mass of \bf{1+2+3}centre of mass of \bf{1+2+3} is at \frac{5\text{w}}{2} from the LHS of \bf{3}, so d3\ =\ \frac{w}{3}.
Thus D\ =\ d_{1}\ +\ d_{2}\ +\ d_{3}\ =\ \left(1\ +\ \frac{1}{2}\ +\ \frac{1}{3}\right)\text{w}\ =1.8\dot{3}\text{w}.
In a similar manner we find that, given n\ +\ 1 books, the maximum overhang is
D\ =\ \left(1+\frac{1}{2}+\frac{1}{3}...\ ...+\frac{1}{n}\right)\text{w}.
I do not know if there is a simple expression for the sum to n terms of this harmonic series. Please let me know if you know of one or can find one. Therefore I used a computer to solve
1+\frac{1}{2}+\frac{1}{3}...\ ...+\frac{1}{n}\ =\ 10
by brute force. I got n = 12367, so you would need 12368 books.
The harmonic series is divergent and has no finite limit, so there is no finite limit to the possible overhang.
You might wish to speculate on any practical limitations on constructing such a pile of books. For example, we have been assuming a uniform gravitational field – but this will no longer be valid once the overhang becomes comparable to the radius of Earth. This will, however, need quite a large number of books.
In the solution that follows, a prime will be used to denote differentiation with respect to x, and p\ =\ y'\ =\ \frac{dy}{dx}. I shall also make use of an auxiliary variable \phi\ =\ \sinh^{-1}p. The initial conditions are y=0,\ x=a,\ p=0,\ \phi=0. The final conditions are x=0,\ p=-\infty,\phi=-\infty,y to be determined.
At time t, the y-coordinate of the Man is v\ t. If (x,\ y) are the coordinates of the Dog at that time, the slope of the path taken by the Dog is
p\ =\ -\frac{vt-y}{x}, \tag{1}\label{36.1}
so that
v\ t\ =\ y-px. \tag{2}\label{36.2}
The speed of the Dog is
A v =\ -\frac{ds}{dt}\ =\ -\sqrt{1+p^{2}}\frac{dx}{dt}. \tag{3}\label{36.3}
[This comes from ds\ =\ \sqrt{1+\left(\frac{dy}{dx}\right)^{2}}dx. The minus sign is necessary because \left(\frac{dx}{dt}\right) is negative, and Av, the speed (not velocity!) of the Dog is necessarily positive.]
Now \left(\frac{dx}{dt}\right)\ =\ -\frac{1}{t'} so Equation ( \ref{eq:36.3}) can be written
Avt'\ =\ -\sqrt{1+p^{2}} \tag{4}\label{36.4}
If we can eliminate t between Equations (\ref{36.2}) and ( \ref{36.4}), we will obtain a relation between the slope p and x, and hence potentially a relation between y and x.
Differentiate Equation ( \ref{eq:36.2)} with respect to x (recalling that y'=p):
vt'\ =\ -p'x \tag{5}\label{36.5}
It is now simple to eliminate t' from Equations ( \ref{36.4}) and ( \ref{36.5}):
Ap'x\ =\ \sqrt{1+p^{2}} \tag{6}\label{36.6}
On separating the variables and integrating, we obtain
A\int\frac{dp}{\sqrt{1+p^{2}}}\ =\ \int\frac{dx}{x}. \tag{7}\label{36.7}
With initial conditions p=0 when x=a, this gives us
A\sinh^{-1}p\ =\ \ln\left(\frac{x}{a}\right), \tag{8}\label{36.8}
or
x\ =\ ae^{A\phi}, \tag{9}\label{36.9}
where
\phi\ =\ \sinh^{-1}p. \tag{10}\label{36.10}
Equation ( \ref{36.9}), with ( \ref{36.10}), gives us the relation between x and the slope, p. Note that p and hence f are negative, so that equation says that x<a.
Our next task will be to find a relation between y and p (or between y and \phi).
From Equation ( \ref{36.10}) we have
dy\ =\ \sinh\phi\ dx, \tag{11}\label{36.11}
and from Equation ( \ref{36.9}) we have
dx\ =\ aAe^{A\phi}d\phi. \tag{12}\label{36.12}
From these we obtain the differential relation between y and \phi:
dy\ =\ aAe^{A\phi}\sinh\phi d\phi, \tag{13}\label{36.13}
or
dy\ =\ \frac{1}{2}aA(e^{(A+1)\phi}\ -\ e^{(A-1)\phi})d\phi. \tag{14}\label{36.14}
Integrate this, with initial condition \phi\ =\ 0 when y\ =\ 0, to obtain
y\ =\ \frac{1}{2}aA\left(\frac{\left(\frac{x}{a}\right)^{1+1/A}}{A+1}-\frac{e^{(A-1)\phi}}{A-1}+\frac{2}{A^{2}-1}\right). \tag{15}\label{36.15}
Equation ( \ref{36.9}) and ( \ref{36.15}) are parametric equations to the path of the Dog, though it is easy to eliminate \phi and write y explicitly as a function of x:
y\ =\ \frac{1}{2}aA\left(\frac{e^{(A+1)\phi}}{A+1}-\frac{e^{(A-1)\phi}}{A-1}+\frac{2}{A^{2}-1}\right). \tag{16}\label{36.16}
The figure was drawn for a=1,\ A=2, for which Equation ( \ref{36.16}) reduces to
y\ =\ \frac{1}{3}[x^{\frac{1}{2}}(x-3)\ +\ 2]. \tag{17}\label{36.17}
The distance walked by the Man is found by putting \phi=-\infty in Equation \ref{36.15}. Thus
y\ =\ \frac{aA}{A^{2}-1}, \tag{18}\label{36.18}
and the time taken is
t\ =\ \frac{aA}{v(A^{2}-1)} \tag{19}\label{36.19}
Let l be the length of the string.
Kinetic energy of the upper mass = \frac{1}{2}(mr^{2})\omega^{2}\ +\frac{1}{2}m\dot{r}^{2}.
Kinetic energy of the lower mass = \frac{1}{2}m\dot{r}^{2}
Potential energy of the lower mass = m\text{g}(l-r).
Total energy of the system =
\frac{1}{2}(mr^{2})\omega^{2}\ + m\dot{r}^{2}\ -\ m\text{g}(l-r). \tag{1}\label{37a.1}
Initial total energy of the system =
\frac{1}{2}(ma^{2})\omega_{0}^{2}\ + m\dot{r}^{2}\ -\ m\text{g}(l-a). \tag{2}\label{37a.2}
Energy is conserved and therefore, by equating ( \ref{37a.1}) and ( \ref{37a.2}), we obtain
\dot{r}^{2}\ =\ \text{g}(a-r)\ +\ \frac{1}{2}a^{2}\omega_{0}^{2}\ -\ \frac{1}{2}r^{2}\omega^{2}. \tag{3}\label{37a.3}
Angular momentum is also conserved, and therefore
r^{2}\omega\ =\ a^{2}\omega_{0} \tag{4}\label{37a.4}
On elimination of r between Equations ( \ref{37a.3}) and ( \ref{37a.4}) we obtain, after some algebra,
\frac{\dot{r}^{2}}{\text{g}a}\ =\ 1\ +\ \frac{a\omega_{0}^{2}}{2\text{g}}\left(1-\frac{\omega}{\omega_{0}}\right)\ -\sqrt{\frac{\omega_{0}}{\omega}}. \tag{5}\label{37a.5} ![]()
If a\omega_{0}^{2}\ =\ \text{g} it is trivial to show that
\frac{\dot{r}^{2}}{\text{g}a}\ =\ \frac{3}{2}\ -\frac{1}{2}\Omega\ -\frac{1}{\sqrt{\Omega }}. \tag{6}\label{37a.6}
Algebra and calculus show that \frac{3}{2}\ -\frac{1}{2}\Omega\ -\frac{1}{\sqrt{\Omega }} is negative for all positive \Omega except for \Omega\ =\ 1, when it reaches a maximum value of zero.
If a\omega_{0}^{2}\ =\ 2\text{g} and \Omega\ =\ \frac{\omega}{\omega_{0}} it is trivial to show that
\frac{\dot{r}^{2}}{\text{g}a}\ =\ 2\ -\ \Omega\ -\frac{1}{\sqrt{\Omega}} \tag{7}\label{37a.7}
Algebra and calculus show that 2\ -\ \Omega\ -\frac{1}{\sqrt{\Omega}} reaches a maximum value for \Omega\ =\ \frac{\omega}{\omega_{0}}\ =\ \frac{1}{2^{\frac{2}{3}}}\ =\ 0.629\ 961 at which time \frac{\dot{r}^{2}}{(\text{g}a)}\ =\ 0.110\ 118. That is, when \dot{r}\ =\ 0.331\ 841\sqrt{\text{g}a} Equation ( \ref{37a.4}) (conservation of angular momentum) shows that r\ =\ \frac{a}{\sqrt{\Omega}}\ =\ \sqrt[3]{2a}\ =\ 1.259\ 921a.
Solution of 2\ -\ \Omega\ -\ \frac{1}{\sqrt{\Omega}}=0 shows that the speed is zero when \Omega\ =\ 1 (the initial condition) and when (the equilibrium value). Equation ( \ref{37a.4}) (conservation of angular momentum) shows that r\ =\ \frac{a}{\sqrt{\Omega}}\ =\ 1.618\ 034a.
If a\omega_{0}^{2}\ =\ \frac{1}{2}\text{g} and \Omega\ =\frac{\omega}{\omega_{0}} it is trivial to show that
\frac{\dot{r}^{2}}{\text{g}a}\ =\ \frac{5}{4}\ -\frac{1}{4}\Omega\ -\frac{1}{\sqrt{\Omega}} \tag{8}\label{37.8}
Algebra and calculus show that \frac{5}{4}\ -\frac{1}{4}\Omega\ -\frac{1}{\sqrt{\Omega}} reaches a maximum value for \Omega\ =\ \frac{\omega}{\omega_{0}}\ =\ 2^{\frac{2}{3}}\ =\ 1.587\ 401 at which time \frac{\dot{r}^{2}}{(\text{g}a)}=0.059449. That is, when \dot{r}\ =\ -0.243\ 822\sqrt{\text{g}a} Equation ( \ref{37a.4}) (conservation of angular momentum) shows that r\ =\ \frac{a}{\sqrt{\Omega}}\ =\ \frac{a}{\sqrt[3]{2}}\ =\ 0.793\ 701a.
Solution of \frac{5}{4}\ -\frac{1}{4}\Omega\ -\frac{1}{\sqrt{\Omega}} shows that the speed is zero when \Omega\ =\ 1 (the initial condition) and when \Omega\ =\ \frac{\omega}{\omega_{0}}\ =\ 2.438\ 447 (the equilibrium value). Equation ( \ref{37a.4}) (conservation of angular momentum) shows that r\ =\ \frac{a}{\sqrt{\Omega}}\ =\ 0.640\ 388a.
How much further can we go with this question? By elimination of r between Equations ( \ref{37a.3}) and ( \ref{37a.4}) we obtained a relation between \dot{r} and \omega. By elimination of \omega between Equations ( \ref{37a.3}) and ( \ref{37a.4}) we can get a relation between \dot{r} and r. It will be of the form
\dot{r}\ =\ \sqrt{A\ -\ \text{g}r\ -\ \frac{B}{r^{2}}}, \tag{9}\label{37a.9}
where A\ =\ \text{g}a\ +\ \frac{1}{2}a^{2}\omega_{0}^{2} and B\ =\ a^{4}\omega_{0}^{4}. If you can integrate this, you then get a relation between r and t. I haven’t given much though as to whether you can get integrate Equation ( \ref{37a.9}) analytically (if anyone manages it, please let me know), but at least a numerical integration will certainly be possible.
In another variation of the question, you can start with an equilibrium situation in which a\omega_{0}^{2}\ =\ \text{g} and then add an extra mass m (or M, if you want to make it more general) and then follow the motion from there. I leave that to you.
Let’s look at the rod from above when it is twisted in the horizontal plane through a small angle \theta.
Each of the points where the threads are attached to the rod is displaced horizontally through a distance \frac{1}{2}D\theta (Since \theta is small and D\ <<L we can neglect the slight vertical rise in the position of the rod.) Each thread is now displaced from the vertical by an angle \phi given by
The tension T in each thread is \frac{1}{2}m\text{g}\cos\phi which, to first order in \phi, is just \frac{1}{2}m\text{g}.
The horizontal component of each of these forces is \frac{1}{2}m\text{g}\sin\phi which, to first order in \phi, is \frac{1}{2}m\text{g}\phi.
Therefore the rod experiences a restoring torque equal to \frac{1}{2}m\text{g}D\phi. But \phi\ =\ \frac{\frac{1}{2}D\theta}{L} and therefore the restoring torque is \frac{m\text{g}D^{2}\theta}{4L}.
The equation of motion is therefore
I\ddot{\theta}\ =\ -\frac{mgD^{2}}{4L}\theta
and consequently the period P of small oscillations is
P\ =\ 2\pi\sqrt{\frac{4LI}{mgD^{2}}}\ =\ \frac{4\pi}{D}\sqrt{\frac{LI}{m\text{g}}}.
If the rod is uniform and of length 2l, its moment of inertia is \frac{1}{3}ml^{2} and in that case the period of small oscillations is
P\ =\ \frac{4\pi l}{D}\sqrt{\frac{L}{3\text{g}}}.
There is no need to remind the reader to check the dimensions of these equations.
When the yo-yo has fallen through a distance x, it has lost potential energy Mgh, and it has gained translational kinetic energy \frac{1}{2}mv^{2} and gained rotational kinetic energy \frac{1}{2}I\omega^{2} where \omega\ =\ \frac{v}{a}. Therefore Mgx\ =\ \frac{1}{2}Mv^{2}\ +\ \frac{1}{2}\ I\left(\frac{v}{a}\right)^{2} from which
v^{2}\ =\ 2\ \cdot\ \frac{Ma^{2}\text{g}}{Ma^{2}\ +\ I}\ \cdot\ x.
Thus, from the usual equations for constant linear acceleration, the acceleration is
\frac{Ma^{2}}{Ma^{2}\ +\ I}\times\text{g}.
The net downward force is M\text{g}-P where P is the tension in the string. This is equal to M times the acceleration, from which we obtain
P\ =\ \frac{1}{Ma^{2}+1}\times M\text{g}.
I have drawn four forces on the yo-yo. Its weight M\text{g}. The tension P in the string. The normal reaction N of the table on the yo-yo. And the frictional force F of the table on the yo-yo. As long as the yo-yo is in contact with the table and there is no vertical acceleration, we must have P\ +\ N\ =\ M\text{g}.
Let us suppose that there is no slipping between the yo-yo and the table, so that the yo-yo rolls to the left. We note that there is a net force F to the left, and a net counterclockwise torque about C equal to Pa-Fb. Thus the yo-yo accelerates to the left at a rate \frac{F}{M} it and experiences a counterclockwise angular acceleration (Pa-Fb)\frac{a}{I}. If there is no slipping, these must be related by \frac{F}{M}=b\times\frac{Pa-Fb}{I}. Thus, if there is no slipping,
F\ =\ \left(\frac{Mab}{I\ +\ Mb^{2}}\right)P. \tag{1}\label{40a.1}
The linear acceleration to the left must be \frac{F}{M}, or
\underline{\underline{\frac{abP}{I+Mb^{2}}}} \tag{2}\label{40a.2}
_________________________
Alternative derivation:
There is a net counterclockwise torque about A equal to Pa. The moment of inertia with respect to A is I\ +\ Mb^{2}. Therefore there is an angular acceleration about A equal to \frac{Pa}{I\ +\ Mb^{2}}. Therefore the linear acceleration of C to the left is \underline{\underline{\frac{abP}{I\ +\ Mb^{2}}}} and the frictional force F is M times this, or F\ =\ \left(\frac{Mab}{I\ +\ Mb^{2}}\right)P.
End of Alternative Derivation.
__________________________
However, if the yo-yo is just about to slip, F\ =\ \mu N\ = \ \mu(M\text{g}-P). Upon substitution of this into Equation ( \ref{40a.1}), we see that the yo-yo will just slip if
P\ =\ \frac{\mu M\text{g}(I\ +\ Mb^{2})}{\mu(I\ +\ Mb^{2})\ +\ Mab}. \tag{3}\label{40a.3}
That is, the yo-yo will roll to the left without slipping if
\underline{\underline{\mu\ >\ \frac{MabP}{(M\text{g}-P)(I+Mb^{2})}}} \tag{4}\label{40a.4}
Its linear acceleration is then given by Equation ( \ref{40a.2}), namely
\underline{\underline{\frac{abP}{I+Mb^{2}}}} \tag{2}\label{40a.2b}
On the other hand, the yo-yo will rotate counterclockwise with no rolling if
\underline{\underline{\mu\ <\ \frac{MabP}{(M\text{g}-P)(I+Mb^{2})}}} \tag{5}\label{40a.5}
The sum of the counterclockwise moments of the forces about C is then Pa-Fb where F=\mu N=\mu(M\text{g}-P). The counterclockwise angular acceleration about C is
\frac{Pa-Fb}{I}\ =\ \underline{\underline{\frac{P(a-\mu b)-\mu M\text{g}}{I}}}. \tag{6}\label{40a.6}
I have drawn the four forces on the yo-yo. Its weight M\text{g}. The normal reaction of the table on the yo-yo, which is also of magnitude M\text{g}. The tension P in the string. And the frictional force F of the table on the yo-yo.
At this point it may not be immediately obvious whether F acts to the left or the right. For example, let us suppose that the coefficient of friction is zero. The force P will result in a translation of the yo-yo to the right together with a clockwise rotation of the yo-yo. So, in which direction does the point A on the circumference of the yo-yo move - to the left or the right? It is hard to say, but one might suppose, qualitatively, that, if the moment of inertia is large, the induced rotation will be sluggish, so that A moves to the right. Whereas if I is small, the induced rotation will be rapid, and A will move to the left in spite of the translational motion of the centre of mass to the right. From this we might conclude that, if \mu\neq 0, F will act to the right if I is small, and F will act to the left if I is large. The following analysis shows that this qualitative expectation is correct.centre of mass to the right. From this we might conclude that, if \mu\neq 0, F will act to the right if I is small, and F will act to the left if I is large. The following analysis shows that this qualitative expectation is correct.
(The reader might find some of the Problems in Section 8.2 of Chapter 8 to be helpful at this point, particularly Problem 2.5.)
For the time being, I have drawn F as if acting towards the left.
Let us suppose there is no slipping and that the yo-yo rolls.
The sum of the clockwise moments of the forces about A is P(a\ +\ b) and the moment of inertia about A is I\ +\ Mb^{2}. The yo-yo therefore undergoes an initial clockwise angular acceleration about A equal to \frac{P(a\ +\ b)}{I+Mb^{2}} and, therefore (if there is no slipping), an initial linear acceleration of C to the right equal to
\underline{\underline{\frac{Pb(a\ +\ b)}{I\ +\ Mb^{2}}}}. \tag{1}\label{40b.1}
The above linear acceleration must equal \frac{(P-F)}{M} from which we obtain
F\ =\ \left(\frac{I-Mab}{I+Mb^{2}}\right)P \tag{2}\label{40b.2}
This shows that the frictional force F acts to the left, as shown, if I\ >\ Mab but if I<Mab the frictional force F acts to the right. This is in agreement with our qualitative expectations, namely that F will act to the left if I is large, and to the right if I is small.
Let is consider three cases in turn: I>Mab,\ I<Mab and I=Mab.
(i) I>Mab
In this case, F acts to the left, as drawn. Provided F<\mu M\text{g} there will be no slipping at A, and the yo-yo will roll to the right without slipping. On recalling Equation ( \ref{40b.2}), we see that the yo-yo will roll to the right without slipping, with a linear acceleration given by Equation ( \ref{40b.1}) if
\underline{\underline{\mu>\left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)}}. \tag{3}\label{40b.3}
The linear acceleration to the right is given by Equation ( \ref{40b.1}), namely
\underline{\underline{\frac{Pb(a\ +\ b)}{I\ +\ Mb^{2}}}}. \tag{1}\label{40b.1b}
However, if
\underline{\underline{\mu<\left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)}}. \tag{4}\label{40b.4}
slipping occurs at A. The frictional force is the no longer given by Equation ( \ref{40b.2}), but is given by
F=\mu M\text{g}, \tag{5}\label{40b.5}
and it acts to the left.
(We are concerned in this problem with the initial motion. Once motion is underway, \mu has to be replaced with the smaller coefficient of kinetic friction.)
The net force to the right is then P-\mu M\text{g} so the linear acceleration of C to the right is
\underline{\underline{\frac{P-\mu M\text{g}}{M}}}. \tag{6}\label{40b.6}
Because of condition ( \ref{40b.4}), this is necessarily positive.
The net clockwise moment of the forces about the centre of mass C is Pa\ +\ \mu M\text{g}b. The yo-yo therefore undergoes a clockwise angular acceleration about C ofcentre of mass C is Pa\ +\ \mu M\text{g}b. The yo-yo therefore undergoes a clockwise angular acceleration about C of
\underline{\underline{\frac{Pa\ +\ \mu M\text{g}b}{I}}}. \tag{7}\label{40b.7}
The linear acceleration to the right of the point A on the circumference of the yo-yo is \frac{P\ -\ \mu M\text{g}}{M}\ -\ b\ \times\ \frac{Pa\ +\ \mu M\text{g}b}{I}, and, because of condition ( \ref{40b.4}), some algebra will show that this is necessarily positive, as expected.
(ii) I<Mab
In this case, F acts to the right, and the linear acceleration is \frac{(P\ +\ F)}{M}. Provided that
\underline{\underline{\mu\ >\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)}}, \tag{8}\label{40b.8}
the yo-yo will roll to the right with a linear acceleration given by Equation ( \ref{40b.1}), namely
\underline{\underline{\frac{Pb(a\ +\ b)}{I\ +\ Mb^{2}}}}. \tag{1}\label{40b.1c}
However, if
\underline{\underline{\mu\ >\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)}}, \tag{9}\label{40b.9}
slipping occurs at A. The frictional force is then given by
F\ =\ \mu M\text{g}, \tag{10}\label{40b.10}
and it acts to the right.
The net force to the right is then P\ +\ \mu M\text{g}, so the linear acceleration to the right is
\underline{\underline{\frac{P\ +\ \mu M\text{g}}{M}}}. \tag{11}\label{40b.11}
The net clockwise moment of the forces about the centre of mass C is . The yo-yo therefore undergoes a clockwise angular acceleration about C ofcentre of mass C is . The yo-yo therefore undergoes a clockwise angular acceleration about C of
\underline{\underline{\frac{Pa\ -\ \mu M\text{g}b}{I}}}. \tag{12}\label{40b.12}
The linear acceleration to the left of the point A on the circumference of the yo-yo is b\times\frac{Pa-\mu M\text{g}b}{I}-\frac{P+\mu M\text{g}}{M}, and, because of condition ( \ref{40b.8}), some algebra will show that this is necessarily positive, as expected.
I=Mab
In this case, F is zero. Whatever the coefficient of friction, even zero, the yo-yo will undergo a linear acceleration \frac{P}{M} to the right (Verify that this is consistent with Equation ( \ref{40b.1}) ), and a clockwise angular acceleration about C equal to \frac{Pa}{I}. The linear acceleration to the right of the point A on the circumference of the yo-yo is
\frac{P}{M}\ -b\times\frac{Pa}{I}
which is zero. The initial linear velocity of the point A is therefore zero.
I have drawn the four forces on the yo-yo. Its weight M\text{g}. The normal reaction of the table on the yo-yo, which is also of magnitude M\text{g}. The tension P in the string. And the frictional force F of the table on the yo-yo. On this occasion (unlike in Problem 40 (b)) there is no question about the direction of F, which is towards the left.
Let us suppose there is no slipping.
The sum of the clockwise moments of the forces about A is \frac{P(b-a)}{I\ +\ Mb^{2}} and the moment of inertia about A is I\ +\ Mb^{2}. The yo-yo therefore undergoes an initial clockwise angular acceleration about A equal to \frac{P(b-a)}{I\ +\ Mb^{2}} and therefore (if there is no slipping) an initial linear acceleration to the right equal to
\underline{\underline{\frac{Pb(b-a)}{I\ +\ Mb^{2}}}}. \tag{1}\label{40c.1}
Additional string therefore becomes wrapped around the axle. (Yes, it really does! I tried it!)
The above linear acceleration must equal \frac{(P-F)}{M} from which we obtain
F\ =\ \left(\frac{I\ +\ Mab}{I\ +\ Mb^{2}}\right)P. \tag{2}\label{40c.2}
Provided F < \mu Mg,there will be no slipping at A, and the yo-yo will roll to the right without slipping. Thus the yo-yo will roll to the right without slipping, with a linear acceleration given by equation (1) if
\underline{\mu> \frac{\left( \frac{I+Mab}{I+Mb^2}\right)}{\left( \frac{P}{Mg}\right)}.} \tag{2}\label{40c.3}
\underline{\mu < \frac{\left( \frac{I+Mab}{I+Mb^2}\right)}{\left( \frac{P}{Mg}\right)}}, \label{40c.4}
F = \mu Mg, \tag{2}\label{40c.5}
\underline{\frac{P- \mu Mg}{M}}.\label{40c.6}
\underline{\frac{Pa- \mu Mgb}{I}} \label{40c.7}
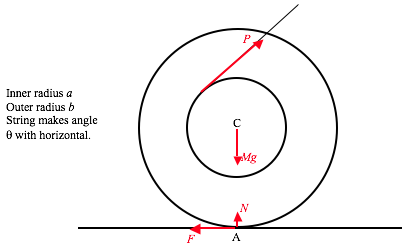
\frac{Pb(a + b \cos \theta}{I+Mb^2} \tag{1}\label{40d.1}
F = \left(\frac{I \cos \theta - Mab}{I+Mb^2}\right)P. \tag{2}\label{40d.2}
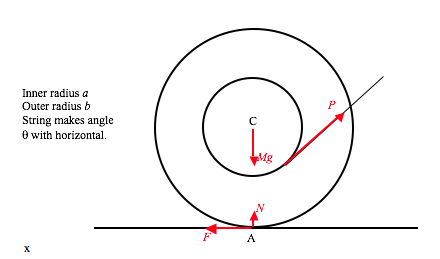
\frac{P(b \cos \theta - a)}{I + Mb^2}. \tag{1}\label{40e.1}
\frac{P(b-\cos \theta - a)}{I + Mb^2}. \tag{2}\label{40e.2}
F = \left(\frac{I \cos \theta + Mab}{I + Mb^2}\right)P, \tag{3}\label{40e.3}
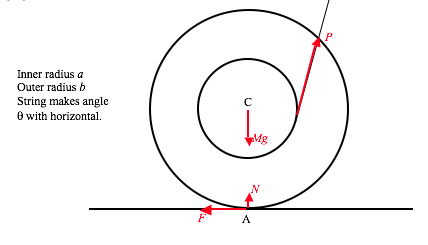
\frac{P(a-b\cos\theta}{I+Mb^2}. \tag{4}\label{40e.4}
\frac{Pb(a-b\cos\theta}{I+Mb^2} \tag{5}\label{40e.5}
F = \left(\frac{I\cos \theta + Mab}{I + Mb^2}\right)P, } \label{40e.6}
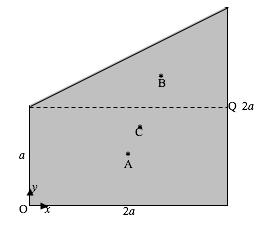
3 m \overline{x} = 2 ma + m \times \frac{4}{3} a
3 m \overline{y} = 2 m \times \frac{1}{2}a + m \times{4}{3} a.
\overline{x} = \frac{10}{9} a \qquad \overline{y} = \frac{7}{9}a.
\frac{1}{2}\begin{bmatrix}x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 &1 \end{bmatrix}.
\frac{1}{3}(2m)(\frac{1}{2} a)^2 = \frac{1}{6} ma^2.
= \frac{1}{3}(2m)a^2 = \frac{2}{3} ma^2.
= 0.
A_{rect} = \frac{1}{6} ma^2 + 2m(\frac{5}{18}a)^2 = \frac{28}{81}ma^2.
B_{rect} = \frac{2}{3} ma^2 + 2m(\frac{1}{9} a)^2 = \frac{65}{81} ma^2
H_{rect} = 0 + 2m(\frac{1}{9}a)(\frac{5}{18}a) = \frac{5}{81} ma^2.
= \frac{1}{6} ma^2 - m(\frac{1}{3}a)^2 = \frac{1}{18}ma^2.
= \frac{1}{6} (m)(2a)^2 - m( \frac{1}{3} \times 2a)^2 = \frac{2}{9}ma^2.
+ \frac{1}{36}m(2a)(a) = +\frac{1}{18} ma^2.
A_{tria} = \frac{1}{18} ma^2 + m(\frac{5}{8} a)^2 = \frac{59}{162}ma^2.
B_{tria} = \frac{2}{9} ma^2 + m(\frac{2}{9} a)^2 = \frac{22}{81}ma^2.
H_{tria} = \frac{1}{18}ma^2 + m(-\frac{2}{9}a)(-\frac{5}{9}a) =\frac{29}{162}ma^2.
A = \frac{26}{81}ma^2 + \frac{59}{162}ma^2 = \frac{37}{51}ma^2.
B = \frac{56}{81}{ma^2+\frac{22}{81}}ma^2 = \frac{26}{27}ma^2.
H = \frac{5}{81}ma^2+\frac{29}{162}m= \frac{13}{54}ma^2.
\theta = 30º.009 180 and 120º.009 180
A \cos^2 \theta - 2 H \sin \theta \cos \theta + b \sin^2 \theta.
A_0 = 0.546142ma2 , B_0= 1.102006ma2.
T = \frac{1}{2} Mx^2 + \frac{1}{2}m(\dot{x}^2 + l^2 \dot{\theta}^2 +2l\dot{\theta}\dot{x} \cos \theta
V = \text{constant} - mgl \cos \theta.
(M+ m)\ddot{x} + ml(\ddot{\theta} \cos \theta - \dot{\theta}^2 \sin \theta) = 0,
l \ddot{\theta} + \ddot{x} + g \theta = 0.
\ddot{\theta} = - \frac{(M+m)g}{Ml}\theta
\underline{\underline{2 \pi = \sqrt{\frac{Ml}{M+m}g}}}.
\frac{1}{k} \frac{dr}{d \alpha} = - \frac{1}{2} \sin \alpha \sin 2 \alpha + 2 \cos^2 \frac{1}{2} \alpha \cos 2 \alpha
= - \sin^2 \alpha \cos \alpha + (1 + \cos \alpha) (2 \cos^2 \alpha -1) = 0.
\underline{\underline{3c^2 + 2c^2 - 2c - 1 = 0}}
The condition for stability, from Chapter 16 Section 16.9, Equation 16.9.5 is that
\frac{Ak^{2}}{V}>\text{HC}.
k^{2} for a filled circle of radius a is \frac{1}{4}a^{2}. If the length of the cylinder is l, the volume immersed is Asl, so the left hand side of the inequality is \frac{a^{2}}{4sl}.
The depth of the centre of mass is l(s-\frac{1}{2}) and the depth of the centre of buoyancy is \frac{1}{2}ls, so that \text{HC}\ =\ \frac{1}{2}l(1-s). The condition for stability is, then, \frac{a^{2}}{4sl}>\frac{1}{2}l(1-s).
With L\ =\frac{l}{(2a)}, this gives, for the condition for stability,
\underline{\underline{L\ <\ \frac{1}{\sqrt{8s(1-s)}}}}
This function is least for s=\frac{1}{2},\ L\ <\ \frac{1}{\sqrt{2}}=0.707. For any length less than this, the system is stable for any density. With L=1, the inequality can be written 8s^{2}-8s+1>0, so that s must be less than 0.146 or greater than 0.854.
Before doing the problem, let’s just have a look at the “interesting” property of a (4, 5, 6) triangle
Calculate A by the cosine rule: 16\ =\ 25\ +\ 36\ -60\cos A, hence \cos A\ =\ \frac{3}{4}.
Calculate C by the cosine rule: 36\ =\ 16\ +\ 25\ -40\cos C, hence \cos C\ =\ \frac{1}{8}.
But \cos 2A\ =\ 2\cos^{2}\ A\ -1\ =\frac{1}{8}. Therefore C\ =\ 2A.
The external angle at B is 3A.
The angles are A\ =\ 41^{\circ}.4096 \quad C\ =\ 82^{\circ}.8192 \quad B\ =\ 55^{\circ}.7711 \quad \left(\cos B=\frac{9}{16}\right)
Supplement of B\ =\ 124^{\circ}.2289
It is not the case that a triangle with one angle equal to twice another one is necessarily a (4, 5, 6) triangle.
After that diversion, let’s move on to the given problem - except that we’ll generalize it to make the length of the rod 2l, and the lengths of the strings a and b.
The only physics involved is to recall that, if three coplanar forces are in equilibrium, they must be concurrent at a point - in this case the point C. This means that C must be vertically above the mid-point of the rod.
After that, there is no more physics; the rest is “just” geometry. All we have to do is to find \theta in terms of a and b.
If C is to be directly above the mid-point, then AN = MB. That is:
b\cos(A+\theta)\ =\ a\cos(B-\theta).
This quickly results in
\tan\theta=\frac{b\cos A\ -\ a\cos B}{b\sin A\ +\ a\sin B}.![]()
In our particular example, \frac{a}{b}\ =\ \frac{4}{5}\ =\ 0.8,\ B\ =\ 180^{\circ}\ -\ 3A, and A\ =\ 41^{\circ}.4096.
Thus
\tan\theta\ =\ \frac{\cos A\ +\ 0.8\cos3A}{\sin A\ +\ 0.8\sin3A},
and
\underline{\theta\ =\ 12^{\circ}.78}
If the weight of the rod is m\text{g}, I’ll leave it to you to work out the tensions in the strings.
The only physics involved is to recall that, if three coplanar forces are in equilibrium, they must be concurrent at a point - in this case the point C. This means that C must be vertically above the mid-point. Also, since the planes are smooth, the forces at A and B are perpendicular to the planes.
The rest is geometry - almost the same as in Problem 45, except that in this problem we are given the angles \alpha and \beta rather than the lengths a and b. Start by convincing yourself that the two angles at C are indeed \alpha and \beta, as marked. Now all that is required is to express \theta in terms of \alpha and \beta.
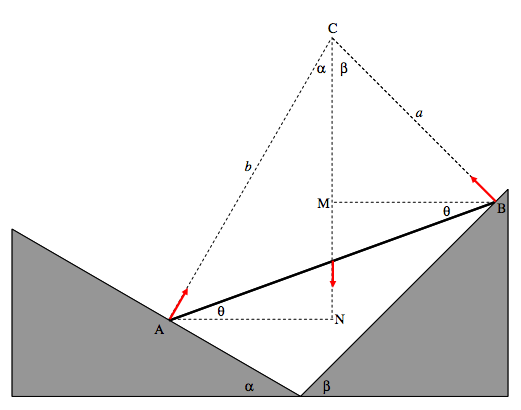
Since the mid-point of the rod must be vertically below C, we must have AN = MB. That is:
b \sin \alpha = a \sin \beta.
By the Sine Rule, \frac{b}{a} = \frac{\sin B}{\sin A}, so that \sin \alpha \sin B = \sin \beta \sin A
But A = 90° - \alpha + \theta and B = 90° -\beta - \theta, so
\sin \alpha = \cos(\beta - \theta) = \sin\beta\cos(\alpha + \theta) ,
which quickly yields \underline{\underline{\tan \theta = \frac{1}{2}(\cot \alpha - \cot \beta)}}. In our particular example, this is \tan \theta = \frac{1}{2}(\sqrt{3} - 1), \underline{\underline{\theta = }}20.1°. If you wish, you could work out the forces at A and B in terms of the weight of the rod.
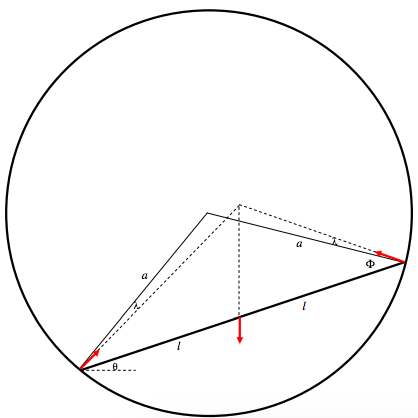
I have drawn above the three forces on the rod. The forces at the ends of the rod each make an angle \lambda to the normal to the surface, where \tan \lambda = \mu, and the three coplanar forces, being in static equilibrium, are concurrent at a point. I have also introduced the angle \phi, given by \cos \phi = l/a. All we have to do is to find \theta in terms of \lambda and \phi - that is to say, in terms of \mu and l/a
Fortunately I found the following formula for a triangle in an old geometry book:
\cot \gamma = \frac{1}{2}(\cos \alpha - \cot \beta)
I’ll leave you to see if you can derive it. The book actually gave a formula for a more general case in which the base of the triangle isn’t divided equally. For the case
the formula is (1+x) \cot \gamma = \cot \alpha - x \cot \beta.
You can use this in various problems in geometric optics, where you are trying to find relations between object distance, image distance and radius of curvature or focal length. However, for this problem, we need only the simpler formula, where the base of the triangle is equally divided.
On applying the simpler formula to our present problem we obtain
\underline{\underline{\tan \theta = \frac{1}{2}[\cot ( \phi - \lambda) - \cot( \phi + \lambda)]}},
and the problem is solved.
Below, I illustrate some examples. Going from left to right we have short l/a=0.2, medium l/a=0.4, long l/a= 0.6 rod. Going from top to bottom we have a slippery \mu = 0.5, a medium /mu = 1.0, and a sticky /mu = 1.5 surface.
Inside each drawing, I tabulate
l/a
/mu
\theta°
The long (l / a =0.6) rod will rest vertically for any /mu > 1.33. But, while it will not slip, the equilibrium is no longer stable, and the rod will tip after an infinitesimal counterclockwise displacement.