22.7: Appendix A

Miscellaneous Problems

In this Appendix I offer a number of random problems in classical mechanics. They are not in any particular order – they come just as I happen to think of them, and they are not necessarily related to any of the topics discussed in any of the chapters. They are intended just to occupy you on those dull, rainy days when you have nothing better to do. Solutions will be in Appendix B – except that whenever I add any new problems to Appendix A, which I shall from time to time, I shall wait a few days before posting the solutions in Appendix B.

_________________________

Exercise \(\PageIndex{1}\)

No book on classical mechanics is complete without a problem of a ladder leaning against a wall. Here, then, is a ladder problem – except that it is nothing whatever to do with mechanics, and it is put here just for fun. It is a problem only in geometry, yet it is one which some people at first find difficult. It even seems difficult to try to find an approximate solution by trying to draw it accurately to scale, and I have deliberately not drawn it to scale, so you can’t find the answer merely by taking a ruler and measuring it!

Two ladders, of lengths 8 m and 10 m, are leaning against two walls as shown. Their point of intersection is 3 m above the ground. What is the distance between the walls?

Exercise \(\PageIndex{2}\)

A pendulum of length \( l_{0}\), is set into motion so that it describes a cone as shown of semi-vertical angle \( \alpha\), the bob describing a horizontal circle at angular speed \( \Omega\)

Show that

\( \cos\alpha=\frac{\text{g}}{l_{0}\Omega^{2}}\).

This, of course, is a very trivial problem not worthy of your mettle. It is given only as an introduction to the next problem.

Exercise \(\PageIndex{3a}\)

A string of a pendulum passes through a board as shown in the figure below, in such a manner that, by lowering or raising the board, the length of the string below the board can be varied. The part below the board is initially of length \( l_{0}\), and it is set into motion as a conical pendulum so that the angular speed and the semi vertical angle are related by

\( \cos\ \alpha=\frac{\text{g}}{l_{0}\Omega^{2}}\).

As the board is raised or lowered (or alternatively the pendulum is lowered or raised) and consequently the length \( l\) below the board is varied, the semivertical angle \( \theta\) will change and so will the angular speed \( \omega\). (The symbols \( l_{0}\), \( \alpha\) and \( \Omega\) represent the initial values of these quantities.)

Show that

1. \( l^{3}\sin^{3}\theta\tan\theta\) is constant,
2. \( \omega^{3}\cot^{2}\theta\) is constant,
3. \( \omega^{3}(\omega l^{2}\ -\ \Omega l_{0}^{2}\sin^{2}\alpha)\) is constant.

Exercise \(\PageIndex{3b}\)

Start with the following initial conditions:

\( l_{0}\ =\ 50\ \text{cm} \qquad \Omega\ =\ 5\ \text{rad s}^{-1}\)

and assume that \( \text{g}\ =\ 9.8\ \text{m s}^{=2}\), so that \( \alpha\ =\ 38^{\circ}\ 22^{\prime}\).

1. Plot a graph of \( \theta\) (vertically) versus \( l\) (horizontally), for \( l\ =\ 0\) to 1 m. When \( l\) = 40 cm, what is \( \theta\) correct to one arcmin?
2. Plot a graph of \( \omega\) (vertically) versus \( \theta\) (horizontally), for \( \theta\) = 0 to 70^o.
3. Plot a graph of \( \omega\) (vertically) versus \( l\) (horizontally) for \( l\) = 16 cm to 1 m. When \( l\) = 60 cm, what is \( \omega\) correct to four significant figures?

________________

The next few problems involve a rod with its lower end in contact with a horizontal table and the rod falling over from an initial vertical (or inclined) position. There are several versions of this problem. The table could be smooth, so that the rod freely slips over the table. Or the lower end could be freely hinged at the table, so that the lower end does not move as the rod falls over. Or the table might be rough, so that the rod might or might not slip.

Exercise \(\PageIndex{4}\)

A uniform rod of mass \( m\) and length \( 2l\) is initially vertical with its lower end in contact with a smooth horizontal table. It is given an infinitesimal angular displacement from its initial position, so that it falls over. When the rod makes an angle \( \theta\) with the vertical, find:

The angular speed of the rod;

The speed at which the centre of the rod is falling;

The speed at which the lower end of the rod is moving;

Show that the speed of the lower end is greatest when \( \theta =\ 37^{\circ}\ 50^{\prime}\).

If the length of the rod is 1 metre, and \( \text{g}\) = 9.8 m s^-2, what is the angle \( \theta\) when the speed of the lower end is 1 m s^-1?

Exercise \(\PageIndex{5}\)

A uniform rod is initially vertical with its lower end smoothly hinged to a horizontal table. Show that, when the rod falls over, the reaction of the hinge upon the rod is vertical when the rod makes an angle 48^o 11' with the vertical, and is horizontal when the rod makes an angle 70^o 31' with the vertical.

Exercise \(\PageIndex{6}\)

A uniform rod of length 1 metre, with its lower end smoothly hinged to a horizontal table, is initially held at rest making an angle of 40^o with the vertical. It is then released. If \( \text{g}\) = 9.8 m s^-1, calculate its angular speed when it hits the table in a horizontal position (easy) and how long it takes to get there (not so easy).

Exercise \(\PageIndex{7}\)

A uniform rod is initially vertical with its lower end in contact with a rough horizontal table, the coefficient of friction being \( \mu\).

Show that:

Exercise \(\PageIndex{7a}\)

If \( \mu\) < 0.3706, the lower end of the rod must slip before the rod makes an angle \( \theta\) with the vertical of 35^o 05'.

Exercise \(\PageIndex{7b}\)

If \( \mu\) > 0.3706, the rod will not slip before \( \theta\) = 51^o 15', but it will certainly slip before \( \theta\) = 70^o 31' .

Exercise \(\PageIndex{7c}\)

If \( \mu\) = 0.25, at what angle \( \theta\) will the lower end slip? If \( \mu\) = 0.75?

Exercise \(\PageIndex{8}\)

It is time for another ladder problem. Most ladders in elementary mechanics problems rest on a rough horizontal floor and lean against a smooth vertical wall. In this problem, both floor and wall are smooth. The ladder starts making an angle of a with the vertical, and then it is released. It immediately starts to slip, of course. After a while it will cease contact with the smooth vertical wall. Show that, at the moment when the upper end of the ladder loses contact with the wall, the angle q that the ladder makes with the vertical is given by \( \cos\theta\ = \frac{2}{3}\cos\alpha\).

Exercise \(\PageIndex{9}\)

If you managed that one all right, this one, which is somewhat similar, should be easy. Maybe.

A uniform solid semicylinder of radius \( a\) and mass \( m\) is placed with its curved surface against a smooth vertical wall and a smooth horizontal floor, its base initially being vertical.

It is then released. Find the reaction \( N_{1}\) of the floor on the semicylinder and the reaction \( N_{2}\) of the wall on the semicylinder when its base makes an angle \( \theta\) with the vertical.

Show that the semicylinder loses contact with the wall when \( \theta\) = 90^o, and that it then continues to rotate until its base makes an angle of 39^o 46' with the vertical before it starts to fall back.

­­­­­­­­­­­­­_________________________

Many problems in elementary mechanics involve a body resting upon or sliding upon an inclined plane. It is time to try a few of these. The first one is very easy, just to get us started. The two following that might be more interesting.

Exercise \(\PageIndex{10}\)

A particle of mass \( m\) is placed on a plane which is inclined to the horizontal at an angle \( \alpha\) that is greater than \( \tan^{-1}\mu\), where \( \mu\) is the coefficient of limiting static friction. What is the least force required to prevent the particle from sliding down the plane?

Exercise \(\PageIndex{11}\)

A cylinder or mass \( m\), radius \( a\), and rotational inertia \( ka^{2}\) rolls without slipping down the rough hypotenuse of a wedge on mass \( M\), the smooth base of which is in contact with a smooth horizontal table. The hypotenuse makes an angle \( \alpha\) with the horizontal, and the gravitational acceleration is \( \text{g}\). Find the linear acceleration of the wedge as it slips along the surface of the table, in terms of \( m,\ M,\ \text{g},\ a,\ k\) and \( \alpha\).

[Note that by saying that the rotational inertia is \( ka^{2}\), I am letting the question apply to a hollow cylinder, or a solid cylinder, or even a hollow or solid sphere.]

Exercise \(\PageIndex{12}\)

A particle is placed on a rough plane inclined at an angle a to the horizontal. It is initially in limiting static equilibrium. It is given an initial velocity \( V_{0}\) along the \( x\)-axis. Ignoring the small difference between the coefficients of moving and limiting static friction, show that at a point on the subsequent trajectory where the tangent to the trajectory makes an angle \( \psi\) with the \( x\)-axis, the speed \( V\) is given by

\( V=\frac{V_{0}}{1+\cos\psi}\)

What is the limiting speed reached by the particle after a long time?

Exercise \(\PageIndex{13}\)

Calculate the moment of inertia of a hollow sphere, mass \( M\), outer radius \( a\), inner radius \( xa\). Express your answer in the form

\( I=\frac{2}{5}Ma^{2}\ \times\ f(x)\).

What does your expression become if \( x=0\)? And if \( x\rightarrow 1\)?

Exercise \(\PageIndex{14}\)

Calculate the moment of inertia of a spherical planet of outer radius \( a\), consisting of a dense core of radius \( xa\) surrounded by a mantle of density \( s\) times the density of the core. Express your answer in the form

\( I=\frac{2}{5}Ma^{2}\times f(x,s)\).

Make sure that, if the density of the core is zero, your expression reduces to the answer you got for Exercise 13.

Draw graphs of \( \frac{I}{(\frac{2}{5}Ma^{2})}\) versus \( x\) (\( x\) going from 0 to 1), for \( s\) = 0.2, 0.4, 0.6 and 0.8.

Show that, for a given mass \( M\) and density ratio \( s\), the moment of inertia is least for a core size give by the solution of

\( 2(I-s)x^{5}+15x^{2}-9=0\)

For a mantle-to-density ratio of 0.6, calculate the core size for which the moment of inertia is least and calculate (in units of \( \frac{2}{5}Ma^{2}\)) the moment of inertia for that core.

Now let’s see if we can determine the core size from a knowledge of the moment of inertia. It is sometimes asserted that one can determine the moment of inertia (and hence the core size) of a planet from the rate of precession of the orbit of a satellite. I am not sure how this would work with a planet such as Mercury, which has never had a satellite in orbit around it. (Mariner 10, while in orbit around the Sun, made three fly-bys past Mercury). Unless a planet departs from spherical symmetry, the orbit of a satellite will not precess, since the gravitational planet is then identical with that from a point mass. And, even if a planet were dynamically oblate, the rate of precession allows us to determine the dynamical ellipticity \( \frac{(C-A)}{C}\), but not either moment of inertia separately.

Nevertheless, let’s suppose that the moment of inertia of a planet is (0.92 ± 1%) % \( \frac{2}{5}Ma^{2}\); specifically, let’s suppose that the moment of inertia has been determined to be between 0.911 and 0.929 % \( \frac{2}{5}Ma^{2}\), and that the mantle-to-core density ratio is known (how?) to be 0.6. Calculate the possible range in the value of the core radius \( x\).

Exercise \(\PageIndex{15}\)

A rectangular brick of length \( 2l\) rests (with the sides of length \( 2l\) vertically) on a rough semicylindrical log of radius \( R\). The drawing below shows three such bricks. In the first one, \( 2l\) is quite short, and it looks is if it is stable. In the second one, \( 2l\) is rather long, and the equilibrium looks decidedly wobbly. In the third one, we’re not quite sure whether the equilibrium is stable or not. What is the longest brick that is stable against small angular displacements from the vertical?

Exercise \(\PageIndex{16}\)

A Thing with a semicylindrical (or hemispherical) base of radius \( a\) is balanced on top of a rough semicylinder (or hemisphere) of radius \( b\) as shown. The distance of the centre of mass of the Thing from the line (or point) of contact is \( l\). Show that the equilibrium is stable if

\( \frac{1}{l}\ >\ \frac{1}{a}+\frac{1}{b}\).

If \( a=b\), is the equilibrium stable if the Thing is

1. A hollow semicylinder?
2. A hollow hemisphere?
3. A uniform solid semicylinder?
4. A uniform solid hemisphere?

Exercise \(\PageIndex{17}\)

A log of square cross-section, sides \( 2a\), rests on two smooth pegs a distance \( 2ka\) apart, one of the diagonals making an angle \( \theta\) with the vertical.

Show that, if \( k\ <\ \frac{1}{\sqrt{8}}\ =\ 0.354\) the only equilibrium position possible is \( \theta\) = 90^o, but that this position is unstable; consequently, following a small displacement, the log will fall out of the pegs. Show that if the pegs are farther apart, with \( 0.354\ <\ k\ <\ 0.500\), three equilibrium positions are possible. Which of them are stable, and which are unstable? If \( k=0.45\), what are the possible equilibrium values of \( \theta\)? Show that, if \( 0.500\ <\ k\ <\ 1.414\), only one equilibrium position is possible, and that it is stable.

Exercise \(\PageIndex{18}\)

A uniform solid hemisphere of radius \( a\) rests in limiting static equilibrium with its curved surface in contact with a smooth vertical wall and a rough horizontal floor (coefficient of limiting static friction \( \mu\)). Show that the base of the hemisphere makes an angle \( \theta\) with the floor, where

\( \sin\ \theta\ =\ \frac{8\mu}{3}\).

Calculate the value of \( \theta\) if (a) \( \mu\ =\ \frac{1}{4}\) and \( \mu\ =\ \frac{3}{8}\).

What happens if \( \mu\ >\ \frac{3}{8}\)?

Exercise \(\PageIndex{19}\)

A uniform rod of length \( 2l\) rocks to and fro on the top of a rough semicircular cylinder of radius \( a\). Calculate the period of small oscillations.

A uniform solid hemisphere of radius \( a\) with its curved surface in contact with a rough horizontal table rocks through a small angle. Show that the period of small oscillations is

\( P\ =\ 2\pi\sqrt{\frac{26a}{15\text{g}}}\).

Exercise \(\PageIndex{21}\)

The density \( \rho\) of a solid sphere of mass \( M\) and radius \( a\) varies with distance \( r\) from the centre as

\( \rho\ =\ \rho_{0}\left(1-\frac{r}{a}\right)\).

Calculate the (second) moment of inertia about an axis through the centre of the sphere. Express your answer in the form of constant % \( Ma^{2}\).

Exercise \(\PageIndex{22}\)

Two identical particles are connected by a light string of length \( 2a\alpha\). The system is draped over a cylinder of radius \( a\) as shown, the coefficient of limiting static friction being \( \mu\). Determine the angle \( \theta\) when the system is in limiting equilibrium and just about to slide.

Exercise \(\PageIndex{23}\)

A mass \( M\) hangs from a light rope which passes over a rough cylinder, the coefficient of friction being \( \mu\) and the angle of lap being \( \alpha\). What is the least value of \( F\), the tension in the upper part of the rope, required to prevent the mass from falling?

Exercise \(\PageIndex{24}\)

A wooden cube floats on water. One of its faces is freely hinged to an axis fixed in the surface of the water. The hinge is fixed at a distance from the top of the face equal to \( x\) times the length of a side. The opposite face is submerged to a distance \( y\) times the length of a side. Find the relative density \( s\) (that is, relative to the density of the water) of the wood in terms of \( x\) and \( y\).

Exercise \(\PageIndex{25}\)

A uniform solid sphere sits on top of a rough semicircular cylinder. It is given a small displacement so that it rolls down the side of the cylinder. Show that the sphere and cylinder part company when the line joining their centres makes an angle 53^o 58' with the vertical.

Exercise \(\PageIndex{26}\)

A student has a triangular sandwich of sides 9 cm, 12 cm, 15 cm. She takes a semicircular bite of radius 3 cm out of the middle of the hypotenuse. Where is the centre of mass of the remainder? Is it inside or outside the bite?

Exercise \(\PageIndex{27}\)

An rubber elastic band is of length \( 2\pi a\) and mass \( m\); the force constant of the rubber is \( k\). The band is thrown in the air, spinning, so that it takes the form of a circle, stretched by the centrifugal force. (This takes much practice, skill and manual dexterity.) Find a relation between its radius and angular speed, in terms of \( a,\ m\) and \( k\).

Exercise \(\PageIndex{28}\)

Most of us have done simple problems on friction at high school or in first year at college or university. You know the sort – a body lies on a rough horizontal table. A force is applied to it. What happens? Try this one.

Find a uniform rod AB. A ruler will do as long as it is straight and not warped. Or a pencil of hexagonal (not circular) cross-section, provided that it is uniform and does not have an eraser at the end. Place it on a rough horizontal table. Gradually apply a horizontal force perpendicular to the rod at the end A until the rod starts to move. The end A will, of course, move forward. Look at the end B – it moves backward. There is a point C somewhere along the rod that is stationary. I.e., the initial motion of the rod is a rotation about the point C. Calculate – and measure – the ratio AC/AB. What is the force you are exerting on A when the rod is just about to move, in terms of its weight and the coefficient of friction?

Exercise \(\PageIndex{29}\)

Some of the more dreaded friction problems are of the “Does it tip or does it slip?” type. This and the following four are examples of this type.

A uniform solid right circular cone of height \( h\) and basal radius \( a\) is placed on an inclined plane whose inclination to the horizontal is gradually increased. The coefficient of limiting static friction is \( \mu\). Does the cone slip, or does it tip?

Exercise \(\PageIndex{30}\)

A cubical block of side \( 2a\) rests on a rough horizontal table, the coefficient of limiting static friction being \( \mu\). A gradually increasing horizontal force is applied as shown at a distance \( x\) above the table. Will the block slip or will it tip? Show that, if \( \mu\ < \frac{1}{2}\), the block will slip whatever the value of \( x\).

Exercise \(\PageIndex{31}\)

A cylindrical log of diameter \( 2a\) and mass \( m\) rests on two rough pegs (coefficient of limiting static friction \( \mu\)) a distance \( 2ka\) apart. A gradually increasing torque \( \tau\) is applied as shown. Does the log slip (i.e. rotate about its axis) or does it tip (about the right hand peg)?

When you’ve done that one, you can try a variant (which I haven’t worked out and haven’t posted a solution) in which a cylinder of radius \( a\) is resting against a kerb (or curb, if you prefer that spelling) of height \( h\), and a torque is applied. Will it tip or will is slip?

Exercise \(\PageIndex{32}\)

This problem reveals the severe limitations of my artistic abilities, but the drawing above, believe it or not, represents a motor car seen from behind. You can see the driver and passenger. The height of the centre of mass is \( h\) and the distance between the wheels is \( 2d\). The car is travelling on a horizontal road surface, coefficient of friction \( \mu\), and is steering to the left in a circle of radius \( R\), the centre of curvature being way off to the left of the drawing. As they gradually increase their speed, will the car slip to the right, or will it tip over the right hand wheel, and at what speed will this disaster take place? Fortunately, driver and passenger were both wearing their seat belts and neither of them was badly hurt, and never again did they drive too fast round a corner.

Exercise \(\PageIndex{33}\)

A uniform rod of length \( 2l\) rests on a table, with a length \( l-a\) in contact with the table, and the remainder, \( l+a\) sticking over the edge – that is, \( a\) is the distance from the edge of the table to the middle of the rod. It is initially prevented from falling by a force as shown. When the force is removed, the rod turns about A. Show that the rod slips when it makes an angle \( \theta\) with the horizontal, where

\( \tan\ \theta\ =\ \frac{2\mu}{2\ +\ 9(\frac{a}{l})^{2}}\)

Here m is the coefficient of limiting static friction at A.

Exercise \(\PageIndex{34}\)

A flexible chain of mass \( m\) and length \( l\) is initially at rest with one half of it resting on a smooth horizontal table, and the other half dangling over the edge:

It is released, so that it starts to slide off the table. At a subsequent time \( t\), a length \( \frac{1}{2}l-x\) remains in contact with the table, the remaining length \( \frac{1}{2}l+x\) hanging vertically, and the speed of the chain is \( v\).

Show that

\( v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2}\),

\( x\ =\ \frac{l(e^{\sqrt{\frac{\text{g}}{lt}}}-1)^{2}}{4e^{\sqrt{\frac{\text{g}}{lt}}}}\)

\( v\ =\ \frac{\sqrt{\text{g}l}(e^{\sqrt{\frac{\text{4g}}{lt}}}-1)}{4e^{\sqrt{\frac{\text{4g}}{lt}}}}\)

Exercise \(\PageIndex{35a}\)

Four books, each of width \( 2w\), are stacked on top of each other in a heap, thus:

What is the maximum possible overhang, \( D\)?

Exercise \(\PageIndex{35b}\)

How many books would be needed to achieve an overhang of \( 10w\)?

Exercise \(\PageIndex{35c}\)

Given an unlimited supply of books, what is the maximum overhang achievable?

Exercise \(\PageIndex{36}\)

The Man and the Dog.

At time \(t = 0\), the Man is at the origin of coordinates, and he starts to walk up the \(y\)-axis at constant speed \(v\). The Dog starts at \((a , 0) \) and runs at constant speed \(Av (v > 1)\) towards the Man. The velocity of the Dog is always directed straight towards the Man. Find an equation for the path pursued by the Dog, and draw a graph of this path. How far has the Man walked when the Dog reaches the Man, and how long does this take?

Exercise \(\PageIndex{37}\)

A particle A of mass \(m\) is attached by a light string to a second particle, B, also of mass \(m\). A rests on a smooth horizontal table, while B hangs vertically through a hole in the table. At time zero, the length of the horizontal portion of the string (i.e. the distance of A from the hole) is a, and A is moving on the table in a horizontal circle of radius a with initial angular speed \( \omega_0\).

At some subsequent time the length of the horizontal portion of the string is \(r\) and the angular speed of A is \( \omega \). Let us denote by the rate of increase of \(r\) with time, which will evidently be negative if B is falling.

Exercise \(\PageIndex{37a }\)

Show that \( \dot{r} \) is given by

\[ \frac{\dot{r}^2}{ga} = 1 + \frac{a \omega^2_0}{2g} \left( 1- \frac{\omega}{\omega_0}\right) - \sqrt{\frac{\omega}{\omega_0}}. \label{eq:1} \]

Exercise \(\PageIndex{37b}\)

Show that, if \(a \omega^2_0 = g \), where \( \Omega = \omega \ \omega_0 \).

\[ \frac{ \dot{r}^2}{ga} = \frac{3}{2} - \frac{1}{2} \Omega - 1 / \sqrt{\Omega} , \label{eq:2} \]

Exercise \(\PageIndex{37c}\)

Show that there is only one value of Ω, namely 1, for which there is a real solution for \( \dot{r} \), namely \( \dot{r} = 0 \). This implies that the system remains in equilibrium, with the radius of the circle, the angular speed of A and the height of B remaining constant, with the centrifugal force on A remaining equal to the weight of B.

Exercise \(\PageIndex{37d }\)

Show that if \( a \omega^2_0 = 2g \),

\( \frac{\dot{r}^2}{ga} = 2 - \Omega - 1 / \sqrt{ \Omega} \)

and that A moves outwards (its angular speed decreasing) and B moves upwards,

reaching a maximum speed of \( \dot{r} = 0.331841 \sqrt{ga} \)

where \( \dot{r} = 1.259921 a \)

when \( \omega = 0.629961 \omega_0, \)

and it reaches an equilibrium when \( \dot{r} = 0 \)

where \( \dot{r} = 1.618034a \)

when \( \omega = 0.381966 \omega_0. \)

Exercise \(\PageIndex{37e}\)

Show that if \( a \omega^2_0 = \frac{1}{2}g\),

\( \frac{ \dot{r}^2}{ga} = \frac{5}{4} - \frac{1}{4} \Omega - 1 / \sqrt{ \Omega} ,\)

and that A moves inwards (its angular speed increasing) and B moves downwards,

reaching a maximum speed of \( \dot{r} = -0.243822 \sqrt{ga} \)

where \( r = 0.793701 a \)

when \( \omega = 1.587401 \omega_0, \)

and it reaches an equilibrium when \( \dot{r} = 0\)

where \( r = 0.640338a\)

when \( \omega = 2.438447 \omega_0. \)

Exercise \(\PageIndex{38}\)

This problem – the bifilar torsion pendulum − was suggested to me by Claude Plathey, who used the method in a practical application to determine the rotational inertia (moment of inertia) of a real nonuniform rod. He also drew my attention to an interesting paper on the determination of the moments of inertia of bodies (such as aircraft!) by the method: naca.larc.nasa.gov/digidoc/re...ACA-TR-467.PDF

A symmetric but not necessarily uniform rod of mass \(m\) and moment of inertia \(I\) is suspended from the ceiling by two light threads each of length \(L\) a distance \(D\) apart \( (D << L )\).The rod is twisted about a vertical axis through its midpoint through a small angle and then released. Find the period of small oscillations in the horizontal plane.

Exercise \(\PageIndex{39}\)

A yo-yo is of mass M and rotational inertia \(I\). The radius of its axle is \(a\), and it falls in the usual way with a length of string wrapped around the axle.

How that its linear acceleration downwards is

\( \frac{Ma^2}{Ma^2 + I} \times g \)

and that the tension in the string i

\(\frac{I}{Ma^2+ 1} \times Mg \)

Exercise \(\PageIndex{40a }\)

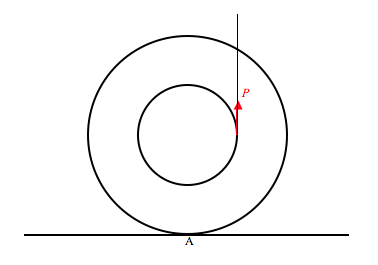
A yo-yo, mass \(M\), axle radius \(a\), outer radius \(b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held vertically as shown, and a force \(P\) is applied. The coefficient of friction between yo-yo and table is \( \mu \). Show that, if

\( \mu > \frac{MabP}{(Mg-P)(I + Mb^2}, \)

the initial motion of the yo-yo will be to roll to the left without slipping, with an initial linear acceleration

\( \frac{abP}{I + Mab} ; \)

but that if

\( \mu < \frac{MabP}{(Mg-P)(I + Mb^2}, \)

the yo-yo will rotate counterclockwise without rolling, with an initial angular acceleration about C of

\( \frac{P(a - \mu) - \mu Mg }{I}. \)

Exercise \(\PageIndex{40b}\)

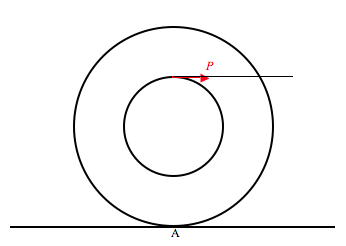
A yo-yo, mass \( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held horizontally as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is \( \mu\).

(i) Show that, if \( I>Mab\):

If

\( \mu\ >\ \left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\)

the initial motion of the yo-yo will be to roll to the right without slipping, with an initial linear acceleration

\( \frac{Pb(a+b)}{I+Mb^{2}}\);

but that, if

\( \mu\ <\ \left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\),

the yo-yo simultaneously accelerates to the right with a linear acceleration of

\( \frac{P-\mu M\text{g}}{M}\)

while undergoing a clockwise angular acceleration about C of

\( \frac{Pa\ +\ \mu M\text{g}b}{I}\).

(ii) Show that, if \( I>Mab\):

If

\( \mu\ >\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)\),

the initial motion of the yo-yo will be to roll to the right without slipping, with an initial linear acceleration

\( \frac{Pb(a+b)}{I+Mb^{2}}\);

but that, if

\( \mu\ <\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)\),

the yo-yo simultaneously accelerates to the right with a linear acceleration of

\( \frac{P\ +\ \mu M\text{g}}{M}\)

while undergoing a clockwise angular acceleration about C of

\( \frac{Pa\ -\ \mu M\text{g}b}{I}\).

(iii) Show that, if \( I>Mab\):

Exercise \(\PageIndex{40c}\)

(After Problem 40(b) this one is a good deal easier and a welcome relief.)

A yo-yo, mass \( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held horizontally as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is m.

Show that, if

\( \mu\ >\ \left(\frac{I+Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\),

the initial motion of the yo-yo will be to roll to the right without slipping, with an initial linear acceleration

\( \frac{Pb(b-a)}{I+Mb^{2}}\)

and angular acceleration

\( \frac{P(b-a)}{I+Mb^{2}}\)

but that, if

\( \mu\ <\ \left(\frac{I+Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\)

the yo-yo slips at A. C accelerates to the right at a rate of \( \frac{P-\mu M\text{g}}{M}\), while the yo-yo spins around C with a counterclockwise angular acceleration of \( \frac{Pa-\mu M\text{g}b}{I}\).

Exercise \(\PageIndex{40d}\)

A yo-yo, mass \( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held at an angle \( \theta\) to the horizontal as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is \( \mu\).

The complete analysis of this problem is similar to that of Problem 40(b), except that a factor of \( \cos\theta\) appears in many of the equations. No new phenomena appear, and the analysis is tedious without any new points of interest. For that reason I limit this problem to asking you to show that the direction of the frictional force of the table on the yo-yo at A depends upon whether the \( \cos\theta\) is less than or greater than \( \frac{Mab}{I}\).

Exercise \(\PageIndex{40e}\)

A yo-yo, mass \( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held at an angle \( \theta\) to the horizontal as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is \( \mu\).

Show that, provided there is no slipping, the yo-yo rolls to the right if \( \cos\theta>\frac{a}{b}\) and to the left if \( \cos\theta<\frac{a}{b}\). Describe what happens if \( \cos\theta=\frac{a}{b}\).

Exercise \(\PageIndex{41}\)

A uniform plane lamina of mass \( 3m\) is in the form of a truncated square like the one above.

Find the position of the centre of mass, the principal moments of inertia with respect to the centre of mass, and the eccentricity and inclination of the momental ellipse.

Exercise \(\PageIndex{42}\)

A mass \( M\) sits on a smooth horizontal table. A second mass, \( m\), hangs from the first by a light inextensible string. A slot in the table allows \( m\) and the string to swing as a pendulum.

The system is then set in motion with the pendulum swinging, and the mass \( M\) sliding back and forth on the table. At some instant when the horizontal displacement of \( M\) from its equilibrium position is \( x\) the string makes an angle \( \theta\) with the vertical.

Show that the equations of motion are

\( (M+m)\ddot{x}\ +\ ml(\ddot{\theta}\cos\theta\ -\ \dot{\theta}^{2}\sin\theta)\ =\ 0\),

\( I\ddot{\theta}\ +\ \ddot{x}\cos\theta\ -\ \dot{x}\sin\theta\dot{\theta}\ =\ -\text{g}\sin\theta\).

Show that for small oscillations \( (\cos\theta\approx 1,\ \sin\theta\approx\theta,\ \dot{\theta}^{2}\theta<<\ddot{\theta},\ \dot{x}\theta\dot{\theta}<<\text{g})\) the period the motion is approximately \( 2\pi\sqrt{\frac{Ml}{(M+m)\text{g}}}\). Note that, if \( m<<M\), this reduces to \( 2\pi\sqrt{\frac{l}{\text{g}}}\) as expected.

Exercise \(\PageIndex{43}\)

A gun projects a shell, in the absence of air resistance, at an initial angle to the horizontal. The speed of projection varies with the angle \( \alpha\) of projection and is given by

initial speed = \( V_{0}\cos\frac{1}{2}\alpha\).

Show that, in order to achieve the greatest range on the horizontal plane, the shell should be projected at an angle to the horizontal whose cosine \( c\) is given by the solution of the equation

\( 3c^{3}+2c^{2}-2c-1=0\)

and determine this angle to the nearest arcminute.

Exercise \(\PageIndex{44}\)

The length of a cylindrical log is \( L\) times its diameter, and its density is \( s\) times that of water \( (0<s<1)\). Show that the log can float vertically in stable equilibrium, whatever its density, provided that \( L<0.707\). and that, if its length is greater than this, it can float vertically in stable equilibrium only if

\( L<\frac{1}{\sqrt{8s(1-s)}}\).

Show that, if the length is equal to the diameter, it can float in stable equilibrium with its cylindrical axis vertical only if its density is less than 0.146 or greater than 0.854 times that of water.

Exercise \(\PageIndex{45}\)

A uniform heavy rod of length 6 hangs from a fixed point C by means of two light strings of lengths 4 and 5. What angle does the rod make with the horizontal?

Incidentally, a (4, 5, 6) triangle has the interesting property that one of its angles is exactly twice one of the other ones.

Exercise \(\PageIndex{46}\)

A uniform rod rests on two smooth (frictionless) planes inclined at 30º and 45º to the horizontal. What angle does the rod make with the horizontal?

Exercise \(\PageIndex{47}\)

A uniform rod of length \( 2l\) rests on the inside of a circular cylindrical pipe of radius \( a\). The coefficient of limiting static friction (often known for short, if with less precision, as “the”coefficient of friction) \( \mu\). What is the maximum angle \( \theta\) that the rod can make with the horizontal in static equilibrium?