3.12: Torque, Angular Momentum and a Moving Point
- Page ID
- 8384
In Figure III.7 I draw the particle \( m_{i}\), which is just one of \( n\) particles, \( n-1\) of which I haven’t drawn and are scattered around in 3-space. I draw an arbitrary origin O, the centre of mass C of the system, and another point Q, which may (or may not) be moving with respect to O. The question I am going to ask is: Does the equation \( \dot{\bf L } = \boldsymbol\tau\) apply to the point Q? It obviously does if Q is stationary, just as it applies to O. But what if Q is moving? If it does not apply, just what is the appropriate relation?
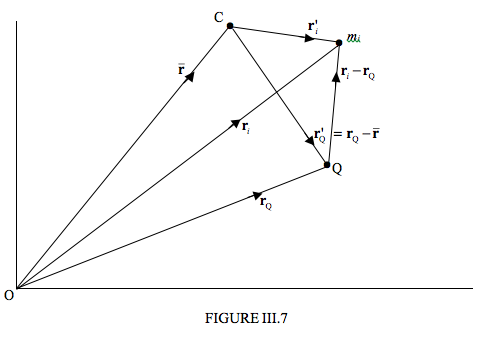
The theorem that we shall prove – and interpret - is
\[ \dot{\bf L }_{Q} = {\boldsymbol\tau}_{Q} + M{\bf r }_{Q}^{\prime} \times\ddot{\bf r}_{Q}. \label{eq:3.12.1} \]
We start:
\[ {\bf L }_{Q} =\sum ({\bf r }_{i} -{\bf r }_{Q})\times [m_{i}({\bf v }_{i}-{\bf v }_{Q})] \label{eq:3.12.2} \]
\[ \therefore \quad \dot{\bf L }_{Q} =\sum ({\bf r }_{i} -{\bf r }_{Q})\times m_{i}(\dot{\bf v }_{i} - \dot{\bf v }_Q)+\sum (\dot{\bf r }_{i} -\dot{\bf r }_{Q})\times m_i({\bf v }_{i} - {\bf v }_Q). \label{eq:3.12.3} \]
The second term is zero, because \( \dot{\bf r}={\bf v}\)
Continue:
\[ \dot{\bf L } =\sum ({\bf r }_{i} -{\bf r }_{Q})\times m_{i}\dot{\bf v }_{i} - \sum m_{i}{\bf r }_{i}\times \dot{\bf v}_{Q} + \sum m_{i}{\bf r }_{Q}\times \dot{\bf v }_{Q} \label{eq:3.12.4} \]
Now \(m_{i} \dot{\bf v }_{i} = {\bf F }_{i}\), so that the first term is just \( {\boldsymbol\tau}_{Q}\)
Continue:
\(\dot{\bf L } = {\boldsymbol\tau}_{Q} - \sum m_{i} {\bf r }_{i} \times dot{\bf v}_{Q} + \sum M_{i} {\bf r }_{Q} \times dot{\bf v }_{Q} \)
\( = {\boldsymbol\tau}_{Q} -M\overline{\bf r }\times \ddot{\bf r }_{Q} +M{\bf r }_{Q}\times \ddot{\bf r }_{Q}\)
\(= {\boldsymbol\tau}_{Q} + M({\bf r }_{Q} - \overline{\bf {\bf r } })\times \ddot{\bf {\bf r } }_{Q}\)
\[ \therefore \dot{\bf L}_{Q} = {\boldsymbol\tau}_{Q} + M{\bf r }^{\prime}_{Q}\times \ddot{r}_{Q} \qquad Q.E. D \label{eq:3.12.5} \]
Thus in general, \(\dot{\bf L}_{Q} \neq {\boldsymbol\tau}_{Q}\), but \(\dot{\bf L}_{Q} = {\boldsymbol\tau}_{Q}\) under any of the following three circumstances:
- \({\bf r }^{\prime}_{Q} = 0\) - that is, Q coincides with C.
- \(\ddot{\bf r }_{Q} = 0\) - that is, Q is not accelerating.
- \(\ddot{\bf r }_{Q}\) and \({\bf r }^{\prime}_{Q}\) are parallel, which would happen, for example, if O were a centre of attraction or repulsion and Q were accelerating towards or away from O.


