3.12: Torque, Angular Momentum and a Moving Point
- Page ID
- 8384
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Figure III.7 I draw the particle \( m_{i}\), which is just one of \( n\) particles, \( n-1\) of which I haven’t drawn and are scattered around in 3-space. I draw an arbitrary origin O, the centre of mass C of the system, and another point Q, which may (or may not) be moving with respect to O. The question I am going to ask is: Does the equation \( \dot{\bf L } = \boldsymbol\tau\) apply to the point Q? It obviously does if Q is stationary, just as it applies to O. But what if Q is moving? If it does not apply, just what is the appropriate relation?
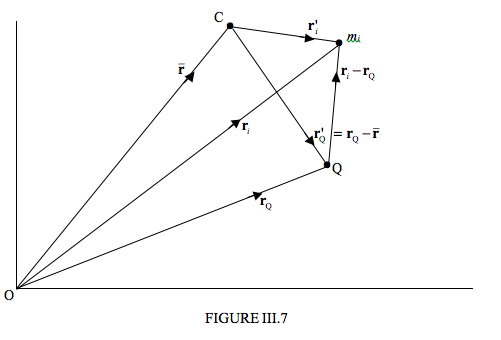
The theorem that we shall prove – and interpret - is
\[ \dot{\bf L }_{Q} = {\boldsymbol\tau}_{Q} + M{\bf r }_{Q}^{\prime} \times\ddot{\bf r}_{Q}. \label{eq:3.12.1} \]
We start:
\[ {\bf L }_{Q} =\sum ({\bf r }_{i} -{\bf r }_{Q})\times [m_{i}({\bf v }_{i}-{\bf v }_{Q})] \label{eq:3.12.2} \]
\[ \therefore \quad \dot{\bf L }_{Q} =\sum ({\bf r }_{i} -{\bf r }_{Q})\times m_{i}(\dot{\bf v }_{i} - \dot{\bf v }_Q)+\sum (\dot{\bf r }_{i} -\dot{\bf r }_{Q})\times m_i({\bf v }_{i} - {\bf v }_Q). \label{eq:3.12.3} \]
The second term is zero, because \( \dot{\bf r}={\bf v}\)
Continue:
\[ \dot{\bf L } =\sum ({\bf r }_{i} -{\bf r }_{Q})\times m_{i}\dot{\bf v }_{i} - \sum m_{i}{\bf r }_{i}\times \dot{\bf v}_{Q} + \sum m_{i}{\bf r }_{Q}\times \dot{\bf v }_{Q} \label{eq:3.12.4} \]
Now \(m_{i} \dot{\bf v }_{i} = {\bf F }_{i}\), so that the first term is just \( {\boldsymbol\tau}_{Q}\)
Continue:
\(\dot{\bf L } = {\boldsymbol\tau}_{Q} - \sum m_{i} {\bf r }_{i} \times dot{\bf v}_{Q} + \sum M_{i} {\bf r }_{Q} \times dot{\bf v }_{Q} \)
\( = {\boldsymbol\tau}_{Q} -M\overline{\bf r }\times \ddot{\bf r }_{Q} +M{\bf r }_{Q}\times \ddot{\bf r }_{Q}\)
\(= {\boldsymbol\tau}_{Q} + M({\bf r }_{Q} - \overline{\bf {\bf r } })\times \ddot{\bf {\bf r } }_{Q}\)
\[ \therefore \dot{\bf L}_{Q} = {\boldsymbol\tau}_{Q} + M{\bf r }^{\prime}_{Q}\times \ddot{r}_{Q} \qquad Q.E. D \label{eq:3.12.5} \]
Thus in general, \(\dot{\bf L}_{Q} \neq {\boldsymbol\tau}_{Q}\), but \(\dot{\bf L}_{Q} = {\boldsymbol\tau}_{Q}\) under any of the following three circumstances:
- \({\bf r }^{\prime}_{Q} = 0\) - that is, Q coincides with C.
- \(\ddot{\bf r }_{Q} = 0\) - that is, Q is not accelerating.
- \(\ddot{\bf r }_{Q}\) and \({\bf r }^{\prime}_{Q}\) are parallel, which would happen, for example, if O were a centre of attraction or repulsion and Q were accelerating towards or away from O.


