4.11: Appendix
- Page ID
- 8883
In Section 4.4 we raised the question as to whether angle is a dimensioned or a dimensionless quantity, and in Section 4.8 we raised the question as to whether angle is a vector quantity.
I can present two arguments. One of them will prove incontrovertibly that angle is dimensionless. The other will prove, equally incontrovertibly, and equally convincingly that angle has dimensions. Angle, as you know, is defined as the ratio of arc length to radius. It is the ratio of two lengths, and is therefore incontrovertibly dimensionless. Q.E.D. On the other hand, it is necessary to state the units in which angle is expressed. You cannot merely talk about an angle of 1. You must state whether that is 1 degree or 1 degree. Angle therefore has dimensions. Q.E.D. So – you may take your pick. In many contexts, I like to think of angle as a dimensioned quantity, having dimensions \( \Theta\). That is to say, not a combination of mass, length and time, but having its own dimensions in its own right. I find I can carry on with dimensional analysis successfully like this.
Now for the question: Is angle a vector?
An angle certainly has both magnitude and a direction associated with it. Thus the direction associated with the angle
is at right angles to the plane of the screen, or the paper.
However, this evidently isn’t enough for it to be a vector in the sense that we know it.
For example, if you turn through an angle a, and then through an angle b, you cannot say that the net resultant of these is to turn through an angle \( c\), where \( c^{2}=a^{2}+b^{2}-2ab\cos C\).
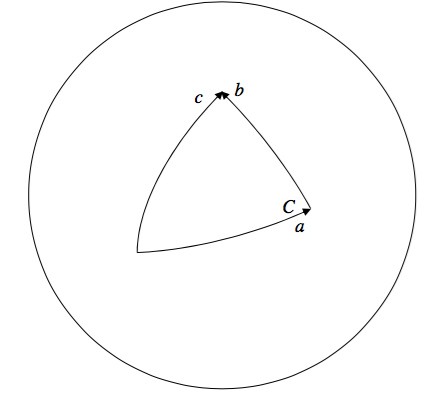
Thus, although angle has both magnitude and direction, and could be thought of thus far as a vector, angles do not obey the ordinary triangle law of vector addition. For this reason, angles are sometimes called “pseudo-vectors”.
In fact, as any astronomy student will tell you, the correct relation between the angles is
\( \cos c=\cos a\cos b+\sin a\sin b\cos C\).
If the angles \( a, b, c\) (not \( C\)) are very small, then the triangle becomes almost plane. The angles add more and more like the usual plane triangle rule for vector addition. This is probably obvious when thinking about the geometry, but you can also convince yourself of it by expanding the sines and cosines (except for \( \cos C\)) as series, and, to the second order of small quantities \( (\cos \theta\approx 1-\frac{1}{2}\theta^{2},\sin\theta\approx 1)\), you’ll find that the equation \( \cos c=\cos a\cos b+\sin a\sin b\cos C\) reduces to \( c^{2}=a^{2}+b^{2}-2ab\cos C\). For this reason it is sometimes said that an “infinitesimal rotation” can
be regarded as a true vector. Also for this reason, the time rate of change of an angle, \( \frac{d\theta}{dt} \), that is to say an angular velocity, can quite safely be treated as a true vector, since the numerator and denominator of the derivatives are both infinitesimals.
Thus, although angle has direction associated with it, angle is not a true vector in that angles do not follow the usual rules for vector addition. However, very small angles do approximately follow the addition rules, so that, in the infinitesimal limit, angles can be treated as vectors. And hence angular velocity, being a ratio of infinitesimals (\( d\theta\) and \( dt\)), can correctly be treated as vectors.


