14.5: Weak Coupling
- Page ID
- 9639
If one of the two coupled linear oscillator masses is held fixed, then the other free mass will oscillate with a frequency.
\[\omega_0 = \sqrt{\dfrac{\kappa + \kappa'}{M}} \label{12.18} \]
The effect of coupling of the two oscillators is to split the degeneracy of the frequency for each mass to
\[\omega_1 = \sqrt{\dfrac{\kappa + 2\kappa'}{M}} > \omega_0 = \sqrt{\dfrac{\kappa + \kappa'}{M}} > \omega_2 = \sqrt{\dfrac{\kappa}{M}} \label{12.19}\]
Thus the degeneracy is broken, and the two normal modes have frequencies straddling the single-oscillator frequency.
It is interesting to consider the case where the coupling is weak because this situation occurs frequently in nature. The coupling is weak if the coupling constant \(\kappa' \ll \kappa\). Then
\[\omega_1 = \sqrt{\dfrac{\kappa + 2\kappa'}{M}} = \sqrt{\dfrac{\kappa'}{M}} \sqrt{1+4\varepsilon} \label{12.20}\]
where
\[ \varepsilon \equiv \dfrac{\kappa'}{2\kappa} \ll 1 \label{12.21}\]
Thus
\[\omega_1 \approx \sqrt{\dfrac{\kappa}{M}} (1 + 2 \varepsilon) \label{12.22}\]
The natural frequency of a single oscillator was shown to be
\[\omega_0 \approx \sqrt{ \dfrac{\kappa + \kappa'}{M}} \approx \sqrt{\dfrac{\kappa }{M}} (1 + \varepsilon) \label{12.23}\]
that is
\[\sqrt{\dfrac{\kappa }{M}} = \omega_o (1 − \varepsilon) \label{12.24}\]
Thus the frequencies for the normal modes for weak coupling can be written as
\[ \begin{align} \omega_1 &= \sqrt{\dfrac{\kappa }{M}} (1 + 2 \varepsilon) \\[5pt] &\approx \omega_0(1 − \varepsilon) (1 + 2\varepsilon) \\[5pt] &\approx \omega_0 (1 + \varepsilon) \label{12.25} \end{align}\]
while
\[\omega_2 = \sqrt{ \dfrac{\kappa }{M}} \approx \omega_0 (1 - \varepsilon) \label{12.26}\]
That is the two solutions are split equally spaced about the single uncoupled oscillator value given by Equation \ref{12.23}. Note that the single uncoupled oscillator frequency \(\omega_0\) depends on the coupling strength \(\kappa'\).
This splitting of the characteristic frequencies is a feature exhibited by many systems of \(n\) identical oscillators where half of the frequencies are shifted upwards and half downward. If \(n\) is odd, then the central frequency is unshifted as illustrated for the case of \(n = 3\). An example of this behavior is the Zeeman effect where the magnetic field couples the atomic motion resulting in a hyperfine splitting of the energy levels of the form illustrated.

There are myriad examples involving weakly-coupled oscillators applied to musical instruments, physics, and engineering. Weakly coupled oscillators are a dominant theme throughout biology as illustrated by congregations of synchronously flashing fireflies, crickets that chirp in unison, an audience clapping at the end of a performance, networks of pacemaker cells in the heart, insulin-secreting cells in the pancreas, and neural networks in the brain and spinal cord that control rhythmic behaviors such as breathing, walking, and eating. Synchronous motion of a large number of weakly-coupled oscillators often leads to large collective motion of weakly-coupled systems as discussed in chapter \(14.12\)
Example \(\PageIndex{1}\): The Grand Piano
The grand piano provides an excellent example of a weakly-coupled harmonic oscillator system that has normal modes. There are either two or three parallel strings per note that are stretched tightly parallel to the top of the horizontal sounding board. The strings press downwards on the bridge that is attached to the top of the sounding board. The strings for each note are excited when struck vertically upwards by a single hammer. In the base section of the piano each note comprises two strings tuned to nearly the same frequency. The coupling of the motion of the strings is via the bridge plus sounding board. Normally, the hammer strikes both strings simultaneously exciting the vertical symmetric mode, not the vertical antisymmetric mode. The bridge is connected to the sounding board which moves the largest amount for the symmetric mode where both strings move the bridge in phase. This strong coupling produces a loud sound. The antisymmetric mode does not move the sounding board much since the strings at the bridge move out of phase. Consequently, the symmetric mode, that is strongly coupled to the sounding board, damps out more rapidly than the antisymmetric mode which is weakly coupled to the sound board and thus has a longer time constant for decay since the radiated sound energy is lower than the symmetric mode.
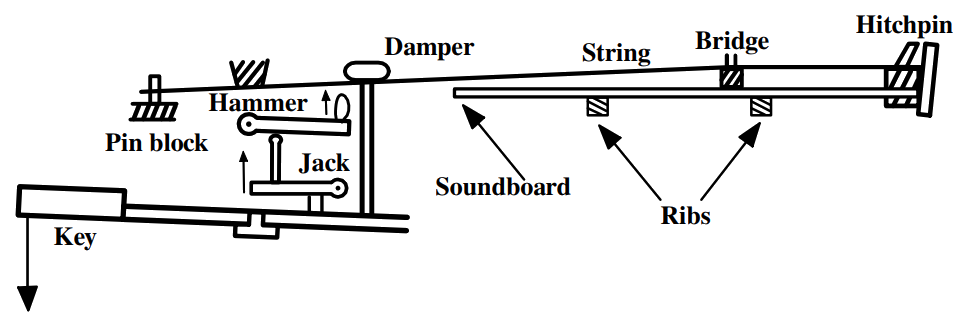
The una-corda pedal (soft pedal) for a grand piano moves the action sideways such that the hammer strikes only one of the two strings, or two of the three strings, resulting in both the symmetric and antisymmetric modes being excited equally. The una-corda pedal produces a characteristically different tone than when the hammer simultaneously hits all the strings; that is, it produces a smaller transient component. The symmetric mode rapidly damps due to energy propagation by the sounding board. Thus the longer lasting antisymmetric mode becomes more prominent when both modes are equally excited using the una-corda pedal. The symmetric and antisymmetric modes have slightly different frequencies and produce beats which also contributes to the different timbre produced using the una-corda pedal. For the mid and upper frequency range, the piano has three strings per note which have one symmetric mode and two separate antisymmetric modes. To further complicate matters, the strings also can oscillate horizontally which couples weakly to the bridge plus sounding board. The strengths that these different modes are excited depend on subtle differences in the shape and roughness of the hammer head striking the strings. Primarily the hammer excites the two vertical modes rather than the horizontal modes.


