18.5: Appendix 18A The Torques About any Two Points are Equal for a Body in Static Equilibrium

When the net force on a body is zero, the torques about any two points are equal. To show this, consider any two points A and B . Choose a coordinate system with origin O and denote the constant vector from A to B by \(\overrightarrow{\mathbf{r}}_{A, B}\). Suppose a force \(\overrightarrow{\mathbf{F}}_{i}\) is acting at the point \(\overrightarrow{\mathbf{r}}_{\mathrm{O}, i}\). The vector from the point A to the point where the force acts is denoted by \(\overrightarrow{\mathbf{r}}_{A, i}\), and the vectors from the point B to the point where the force acts is denoted by \(\overrightarrow{\mathbf{r}}_{B, i}\).

Figure 18A.1 Location of body i with respect to the points A and B .

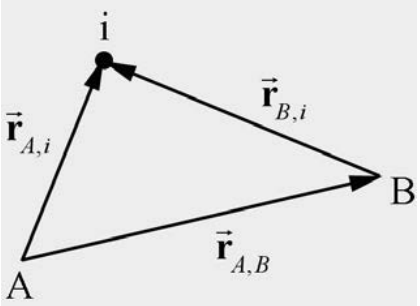
In Figure 18A.1, the position vectors satisfy

\[\overrightarrow{\mathbf{r}}_{A, i}=\overrightarrow{\mathbf{r}}_{A, B}+\overrightarrow{\mathbf{r}}_{B, i} \nonumber \]

The sum of the torques about the point A is given by

\[\vec{\tau}_{A}=\sum_{i=1}^{i=N} \overrightarrow{\mathbf{r}}_{A, i} \times \overrightarrow{\mathbf{F}}_{i} \nonumber \]

The sum of the torques about the point B is given by

\[\vec{\tau}_{B}=\sum_{i=1}^{i=N} \overrightarrow{\mathbf{r}}_{B, i} \times \overrightarrow{\mathbf{F}}_{i} \nonumber \]

We can now substitute Equation (18.A.1) into Equation (18.A.2) and find that

\[\vec{\tau}_{A}=\sum_{i=1}^{i=N} \overrightarrow{\mathbf{r}}_{A, i} \times \overrightarrow{\mathbf{F}}_{i}=\sum_{i=1}^{i=N}\left(\overrightarrow{\mathbf{r}}_{A, B}+\overrightarrow{\mathbf{r}}_{B, i}\right) \times \overrightarrow{\mathbf{F}}_{i}=\sum_{i=1}^{i=N} \overrightarrow{\mathbf{r}}_{A, B} \times \overrightarrow{\mathbf{F}}_{i}+\sum_{i=1}^{i=N} \overrightarrow{\mathbf{r}}_{B, i} \times \overrightarrow{\mathbf{F}}_{i} \nonumber \]

In the next-to-last term in Equation (18.A.4), the vector \(\overrightarrow{\mathbf{r}}_{A, B}\) is constant and so may be taken outside the summation,

\[\sum_{i=1}^{i=N} \overrightarrow{\mathbf{r}}_{A, B} \times \overrightarrow{\mathbf{F}}_{i}=\overrightarrow{\mathbf{r}}_{A, B} \times \sum_{i=1}^{i=N} \overrightarrow{\mathbf{F}}_{i} \nonumber \]

We are assuming that there is no net force on the body, and so the sum of the forces on the body is zero,

\[\sum_{i=1}^{i=N} \overrightarrow{\mathbf{F}}_{i}=\overrightarrow{\mathbf{0}} \nonumber \]

Therefore the torque about point A , Equation (18.A.2), becomes

\[\vec{\tau}_{A}=\sum_{i=1}^{i=N} \overrightarrow{\mathbf{r}}_{B, i} \times \overrightarrow{\mathbf{F}}_{i}=\vec{\tau}_{B} \nonumber \]

For static equilibrium problems, the result of Equation (18.A.7) tells us that it does not matter which point we use to determine torques. In fact, note that the position of the chosen origin did not affect the result at all. Choosing the point about which to calculate torques (variously called “ A ”, “ B ”, “ \(S\) ” or sometimes “O ”) so that unknown forces do not exert torques about that point may often greatly simplify calculations.