24.3: Worked Examples

Example 24.1 Oscillating Rod

A physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. The pendulum is initially displaced to one side by a small angle $\theta_{0}$ and released from rest with $\theta_{0}<<1$. Find the period of the pendulum. Determine the period of the pendulum using (a) the torque method and (b) the energy method.

Figure 24.3 Oscillating rod

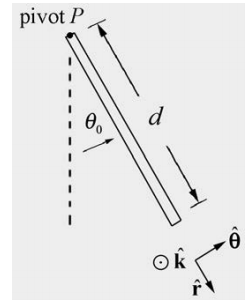
(a) Torque Method: with our choice of rotational coordinate system the angular acceleration is given by

$$\vec{\alpha}=\frac{d^{2} \theta}{d t^{2}} \hat{\mathbf{k}} \nonumber$$

The force diagram on the pendulum is shown in Figure 24.4. In particular, there is an unknown pivot force and the gravitational force acts at the center of mass of the rod.

Figure 24.4 Free-body force diagram on rod

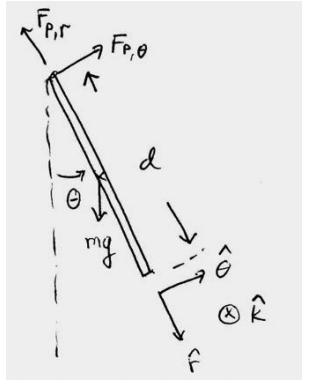
The torque about the pivot point P is given by

$$\overrightarrow{\mathfrak{\tau}}_{P}=\overrightarrow{\mathbf{r}}_{P, \mathrm{cm}} \times m \overrightarrow{\mathrm{g}} \nonumber$$

The rod is uniform, therefore the center of mass is a distance d / 2 from the pivot point. The gravitational force acts at the center of mass, so the torque about the pivot point P is given by

$$\overrightarrow{\boldsymbol{\tau}}_{P}=(d / 2) \hat{\mathbf{r}} \times m g(-\sin \theta \hat{\boldsymbol{\theta}}+\cos \hat{\mathbf{r}})=-(d / 2) m g \sin \theta \hat{\mathbf{k}} \nonumber$$

The rotational equation of motion about P is then

$$\overrightarrow{\boldsymbol{\tau}}_{P}=I_{P} \overrightarrow{\boldsymbol{\alpha}} \nonumber$$

Substituting Equations (24.3.3) and (24.3.1) into Equation (24.3.4) yields

$$-(d / 2) m g \sin \theta \hat{\mathbf{k}}=I_{P} \frac{d^{2} \theta}{d t^{2}} \hat{\mathbf{k}} \nonumber$$

When the angle of oscillation is small, we may use the small angle approximation $\sin \theta \cong \theta$, then Equation (24.3.5) becomes

$$\frac{d^{2} \theta}{d t^{2}}+\frac{(d / 2) m g}{I_{P}} \theta \simeq 0 \nonumber$$

which is a simple harmonic oscillator equation. The angular frequency of small oscillations for the pendulum is

$$\omega_{0} \simeq \sqrt{\frac{(d / 2) m g}{I_{P}}} \nonumber$$

The moment of inertia of a rod about the end point P is $I_{P}=(1 / 3) m d^{2}$ therefore the angular frequency is

$$\omega_{0} \simeq \sqrt{\frac{(d / 2) m g}{(1 / 3) m d^{2}}}=\sqrt{\frac{(3 / 2) g}{d}} \nonumber$$

with period

$$T=\frac{2 \pi}{\omega_{0}} \simeq 2 \pi \sqrt{\frac{2}{3} \frac{d}{g}} \nonumber$$

(b) Energy Method: Take the zero point of gravitational potential energy to be the point where the center of mass of the pendulum is at its lowest point (Figure 24.5), that is, $\theta=0$

Figure 24.5 Energy diagram for rod

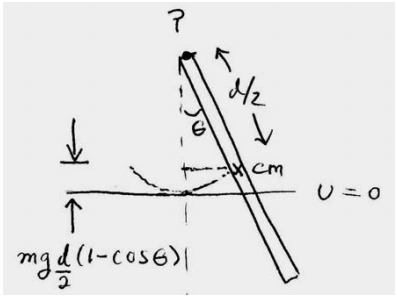
When the pendulum is at an angle θ the potential energy is

$$U=m g \frac{d}{2}(1-\cos \theta) \nonumber$$

The kinetic energy of rotation about the pivot point is

$$K^{\mathrm{rot}}=\frac{1}{2} I_{p} \omega_{z}^{2} \nonumber$$

The mechanical energy is then

$$E=U+K^{\mathrm{rot}}=m g \frac{d}{2}(1-\cos \theta)+\frac{1}{2} I_{p} \omega_{z}^{2} \nonumber$$

with $I_{P}=(1 / 3) m d^{2}$. There are no non-conservative forces acting (by assumption), so the mechanical energy is constant, and therefore the time derivative of energy is zero,

$$0=\frac{d E}{d t}=m g \frac{d}{2} \sin \theta \frac{d \theta}{d t}+I_{p} \omega_{z} \frac{d \omega_{z}}{d t} \nonumber$$

$\text { Recall that } \omega_{z}=d \theta / d t \text { and } \alpha_{z}=d \omega_{z} / d t=d^{2} \theta / d t^{2}$, so Equation (24.3.13) becomes

$$0=\omega_{z}\left(m g \frac{d}{2} \sin \theta+I_{p} \frac{d^{2} \theta}{d t^{2}}\right) \nonumber$$

There are two solutions, $\omega_{z}=0$, in which case the rod remains at the bottom of the swing,

$$0=m g \frac{d}{2} \sin \theta+I_{p} \frac{d^{2} \theta}{d t^{2}} \nonumber$$

Using the small angle approximation, we obtain the simple harmonic oscillator equation (Equation (24.3.6))

$$\frac{d^{2} \theta}{d t^{2}}+\frac{m g(d / 2)}{I_{p}} \theta \simeq 0 \nonumber$$

Example 24.3 Torsional Oscillator

A disk with moment of inertia about the center of mass $I_{\mathrm{cm}}$ rotates in a horizontal plane. It is suspended by a thin, massless rod. If the disk is rotated away from its equilibrium position by an angle θ , the rod exerts a restoring torque about the center of the disk with magnitude given by $\tau_{\mathrm{cm}}=b \theta$ (Figure 24.6), where b is a positive constant. At t = 0 , the disk is released from rest at an angular displacement of $\theta_{0}$. Find the subsequent time dependence of the angular displacement $\theta(t)$.

Figure 24.6 Example 24.3 with exaggerated angle θ

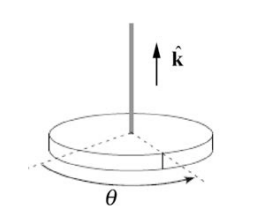
Solution: Choose a coordinate system such that $\hat{\mathbf{k}}$ is pointing upwards (Figure 24.6), then the angular acceleration is given by

$$\overrightarrow{\boldsymbol{\alpha}}=\frac{d^{2} \theta}{d t^{2}} \hat{\mathbf{k}} \nonumber$$

The torque about the center of mass is given in the statement of the problem as a restoring torque, therefore

$$\vec{\tau}_{\mathrm{cm}}=-b \theta \hat{\mathbf{k}} \nonumber$$

The z -component of the rotational equation of motion is

$$-b \theta=I_{\mathrm{cm}} \frac{d^{2} \theta}{d t^{2}} \nonumber$$

This is a simple harmonic oscillator equation with solution

$$\theta(t)=A \cos \left(\omega_{0} t\right)+B \sin \left(\omega_{0} t\right) \nonumber$$

where the angular frequency of oscillation is given by

$$\omega_{0}=\sqrt{b / I_{\mathrm{cm}}} \nonumber$$

The z -component of the angular velocity is given by

$$\omega_{z}(t)=\frac{d \theta}{d t}(t)=-\omega_{0} A \sin \left(\omega_{0} t\right)+\omega_{0} B \cos \left(\omega_{0} t\right) \nonumber$$

The initial conditions at $t=0, \text { are } \theta(t=0)=A=\theta_{0}, \text { and }(d \theta / d t)(t=0)=\omega_{0} B=0$. Therefore,

$$\theta(t)=\theta_{0} \cos (\sqrt{b / I_{\mathrm{cm}}} t) \nonumber$$

Example 24.4 Compound Physical Pendulum

A compound physical pendulum consists of a disk of radius R and mass $m_{d}$ fixed at the end of a rod of mass $m_{r}$ and length $l$ (Figure 24.7a). (a) Find the period of the pendulum. (b) How does the period change if the disk is mounted to the rod by a frictionless bearing so that it is perfectly free to spin?

Figure 24.7 (a) Example 24.4 (b) Free-body force diagram

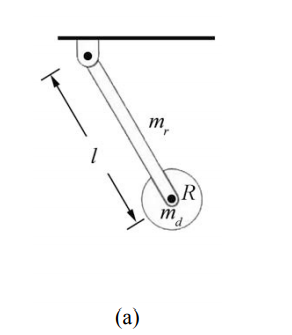
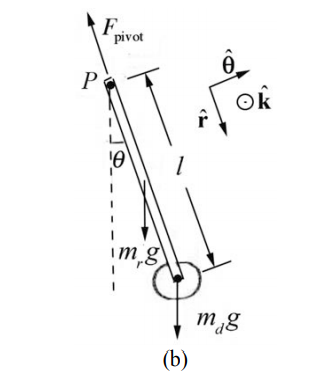
Solution: We begin by choosing coordinates. Let $\hat{\mathbf{k}}$ be normal to the plane of the motion of the pendulum pointing out of the plane of the Figure 24.7b. Choose an angle variable θ such that counterclockwise rotation corresponds to a positive z -component of the angular velocity. Thus a torque that points into the page has a negative z -component and a torque that points out of the page has a positive z -component. The free-body force diagram on the pendulum is also shown in Figure 24.7b. In particular, there is an unknown pivot force, the gravitational force acting at the center of mass of the rod, and the gravitational force acting at the center of mass of the disk. The torque about the pivot point is given by

$$\overrightarrow{\mathbf{\tau}}_{P}=\overrightarrow{\mathbf{r}}_{P, \mathrm{cm}} \times m_{r} \overrightarrow{\mathbf{g}}+\overrightarrow{\mathbf{r}}_{P, \mathrm{disk}} \times m_{d} \overrightarrow{\mathbf{g}} \nonumber$$

Recall that the vector $\overrightarrow{\mathbf{r}}_{P, \mathrm{cm}}$ points from the pivot point to the center of mass of the rod a distance $l / 2$ from the pivot. The vector r points from the pivot point to the center of P, disk mass of the disk a distance l from the pivot. Torque diagrams for the gravitational force on the rod and the disk are shown in Figure 24.8. Both torques about the pivot are in the negative $\hat{\mathbf{k}}$ -direction (into the plane of Figure 24.8) and hence have negative z - components,

$$\overrightarrow{\mathbf{\tau}}_{P}=-\left(m_{r}(l / 2)+m_{d} l\right) g \sin \theta \hat{\mathbf{k}} \nonumber$$

Figure 24.8 Torque diagram for (a) center of mass, (b) disk

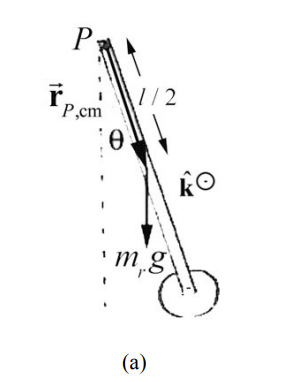
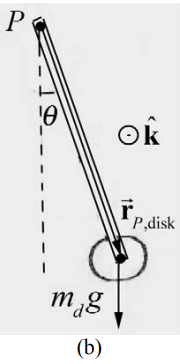
In order to determine the moment of inertia of the rigid compound pendulum we will treat each piece separately, the uniform rod of length d and the disk attached at the end of the rod. The moment of inertia about the pivot point P is the sum of the moments of inertia of the two pieces,

$$I_{P}=I_{P, \text { rod }}+I_{P, \text { disc }} \nonumber$$

We calculated the moment of inertia of a rod about the end point P (Chapter 16.3.3), with the result that

$$I_{P, \mathrm{rod}}=\frac{1}{3} m_{r} l^{2} \nonumber$$

We can use the parallel axis theorem to calculate the moment of inertia of the disk about the pivot point P,

$$I_{P, \text { disc }}=I_{\mathrm{cm}, \text { disc }}+m_{d} l^{2} \nonumber$$

We calculated the moment of inertia of a disk about the center of mass (Example 16.3) and determined that

$$I_{\mathrm{cm}, \mathrm{disc}}=\frac{1}{2} m_{d} R^{2} \nonumber$$

The moment of inertia of the compound system is then

$$I_{P}=\frac{1}{3} m_{r} l^{2}+m_{d} l^{2}+\frac{1}{2} m_{d} R^{2} \nonumber$$

Therefore the rotational equation of motion becomes

$$-\left((1 / 2) m_{r}+m_{d}\right) g l \sin \theta \hat{\mathbf{k}}=\left(\left((1 / 3) m_{r}+m_{d}\right) l^{2}+(1 / 2) m_{d} R^{2}\right) \frac{d^{2} \theta}{d t^{2}} \hat{\mathbf{k}} \nonumber$$

When the angle of oscillation is small, we can use the small angle approximation $\sin \theta \simeq \theta$. Then Equation (24.3.31) becomes a simple harmonic oscillator equation,

$$\frac{d^{2} \theta}{d t^{2}} \simeq-\frac{\left((1 / 2) m_{r}+m_{d}\right) g l}{\left((1 / 3) m_{r}+m_{d}\right) l^{2}+(1 / 2) m_{d} R^{2}} \theta \nonumber$$

Equation (24.3.32) describes simple harmonic motion with an angular frequency of oscillation when the disk is fixed in place given by

$$\omega_{\text {fixed }}=\sqrt{\frac{\left((1 / 2) m_{r}+m_{d}\right) g l}{\left((1 / 3) m_{r}+m_{d}\right) l^{2}+(1 / 2) m_{d} R^{2}}} \nonumber$$

The period is

$$T_{\text {fixed }}=\frac{2 \pi}{\omega_{\text {fired }}} \simeq 2 \pi \sqrt{\frac{\left((1 / 3) m_{r}+m_{d}\right) l^{2}+(1 / 2) m_{d} R^{2}}{\left((1 / 2) m_{r}+m_{d}\right) g l}} \nonumber$$

(b) If the disk is not fixed to the rod, then it will not rotate about its center of mass as the pendulum oscillates. Therefore the moment of inertia of the disk about its center of mass does not contribute to the moment of inertia of the physical pendulum about the pivot point. Notice that the pendulum is no longer a rigid body. The total moment of inertia is only due to the rod and the disk treated as a point like object,

$$I_{P}=\frac{1}{3} m_{r} l^{2}+m_{d} l^{2} \nonumber$$

Therefore the period of oscillation is given by

$$T_{\text {fire }}=\frac{2 \pi}{\omega_{\text {free }}} \simeq 2 \pi \sqrt{\frac{\left((1 / 3) m_{r}+m_{d}\right) l^{2}}{\left((1 / 2) m_{r}+m_{d}\right) g l}} \nonumber$$

Comparing Equation (24.3.36) to Equation (24.3.34), we see that the period is smaller when the disk is free and not fixed. From an energy perspective we can argue that when the disk is free, it is not rotating about the center of mass. Therefore more of the gravitational potential energy goes into the center of mass translational kinetic energy than when the disk is free. Hence the center of mass is moving faster when the disk is free so it completes one period is a shorter time.