26.4: Elastic and Plastic Deformation

Consider a single sheet of paper. If we bend the paper gently, and then release the constraining forces, the sheet will return to its initial state. This process of gently bending is reversible as the paper displays elastic behavior. The internal forces responsible for the deformation are conservative. Although we do not have a simple mathematical model for the potential energy, we know that mechanical energy is constant during the bending. We can take the same sheet of paper and crumple it. When we release the paper it will no longer return to its original sheet but will have a permanent deformation. The internal forces now include non-conservative forces and the mechanical energy is decreased. This plastic behavior is irreversible.

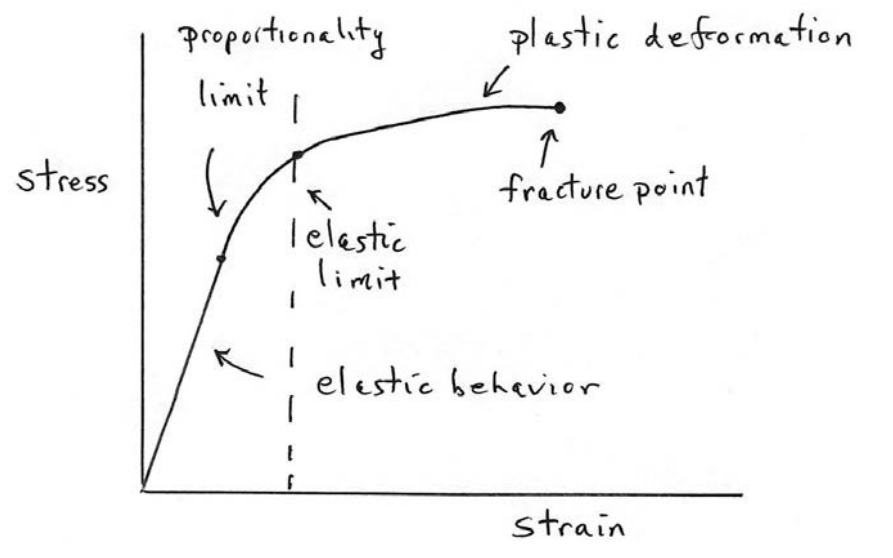
Figure 26.5: Stress-strain relationship

When the stress on a material is linearly proportional to the strain, the material behaves according to Hooke’s Law. The proportionality limit is the maximum value of stress at which the material still satisfies Hooke’s Law. If the stress is increased above the proportionality limit, the stress is no longer linearly proportional to the strain. However, if the stress is slowly removed then the material will still return to its original state; the material behaves elastically. If the stress is above the proportionality limit, but less then the elastic limit, then the stress is no longer linearly proportional to the strain. Even in this non-linear region, if the stress is slowly removed then the material will return to its original state. The maximum value of stress in which the material will still remain elastic is called the elastic limit. For stresses above the elastic limit, when the stress is removed the material will not return to its original state and some permanent deformation sets in, a state referred to as a permanent set. This behavior is referred to as plastic deformation. For a sufficiently large stress, the material will fracture. Figure 26.5 illustrates a typical stress-strain relationship for a material. The value of the stress that fractures a material is referred to as the ultimate tensile strength. The ultimate tensile strengths for various materials are listed in Table 26.3. The tensile strengths for wet human bones are for a person whose age is between 20 and 40 years old.

Table 26.3: Ultimate Tensile Strength for Various Materials

\begin{equation}\begin{array}{|l|l|}
\hline \text { Material } & \text { Shear Modulus, } \(S\) \text { (Pa) } \\
\hline \text { Femur } & 1.21 \times 10^{8} \\
\hline \text { Humerus } & 1.22 \times 10^{8} \\
\hline \text { Tibia } & 1.40 \times 10^{8} \\
\hline \text { Fibula } & 1.46 \times 10^{8} \\
\hline \text { Ulna } & 1.48 \times 10^{8} \\
\hline \text { Radius } & 1.49 \times 10^{8} \\
\hline \text { Aluminum } & 2.2 \times 10^{8} \\
\hline \text { Iron } & 3.0 \times 10^{8} \\
\hline \text { Brass } & 4.7 \times 10^{8} \\
\hline \text { Steel } & 5-20 \times 10^{8} \\
\hline
\end{array}\end{equation}

Example 26.2: Ultimate Tensile Strength of Bones

The ultimate tensile strength of the wet human tibia (for a person of age between 20 and 40 years) is \(1.40 \times 10^{8} \mathrm{Pa}\). If a greater compressive force per area is applied to the tibia then the bone will break. The smallest cross sectional area of the tibia, about\(3.2 \mathrm{cm}^{2}\) is slightly above the ankle. Suppose a person of mass 60 kg jumps to the ground from a height 2.0 m and absorbs the shock of hitting the ground by bending the knees. Assume that there is constant deceleration during the collision. During the collision, the person lowers her center of mass by an amount d = 1.0 cm . (a) What is the collision time \(\Delta t_{\mathrm{col}}\)? (b) Find the average force of the ground on the person during the collision. (c) Can we effectively ignore the gravitational force during the collision? (d) Will the person break her ankle? (e) What is the minimum distance \(\Delta d_{\min }\) that she would need to lower her center of mass so she does not break her ankle? What is the ratio \(h_{0} / \Delta d_{\min }\)? What factors does this ratio depend on?

Solution: Choose a coordinate system with the positive y -direction pointing up, and the origin at the ground. While the person is falling to the ground, mechanical energy is constant (we are neglecting any non-conservative work due to air resistance). Choose the contact point with the ground as the zero potential energy reference point. Then the initial mechanical energy is

\begin{equation}E_{0}=U_{0}=m g h_{0}\end{equation}

The mechanical energy of the person just before contact with the ground is

\begin{equation}E_{b}=K_{1}=\frac{1}{2} m v_{b}^{2}\end{equation}

The constancy of mechanical energy implies that

\begin{equation}m g h_{0}=\frac{1}{2} m v_{b}^{2}\end{equation}

The speed of the person the instant contact is made with the ground is then

\begin{equation}v_{b}=\sqrt{2 g h_{0}}\end{equation}

If we treat the person as the system then there are two external forces acting on the person, the gravitational force \(\overrightarrow{\mathbf{F}}^{g}=-m g \hat{\mathbf{j}}\) and a normal force between the ground and the person \(\overrightarrow{\mathbf{F}}^{N}=N \hat{\mathbf{j}}\). This force varies with time but we shall consider the time average \(\overrightarrow{\mathbf{F}}_{\mathrm{ave}}^{N}=N_{\mathrm{ave}} \hat{\mathbf{j}}\). Then using Newton’s Second Law,

\begin{equation}N_{\text {ave }}-m g=m a_{y, \text { ave }}\end{equation}

The y -component of the average acceleration is equal to

\begin{equation}a_{y, \text { ave }}=\frac{N_{\text {ave }}}{m}-g\end{equation}

Set t = 0 for the instant the person reaches the ground; then \(v_{y, 0}=-v_{b}\). The displacement of the person while in contact with the ground for the time interval \(\Delta t_{\mathrm{col}}\) is given by

\begin{equation}\Delta y=-v_{b} \Delta t_{\mathrm{col}}+\frac{1}{2} a_{y, \mathrm{ave}} \Delta t_{\mathrm{col}}^{2}\end{equation}

The y -component of the velocity is zero at \(t=\Delta t_{\mathrm{col}}\) when the person’s displacement is \(\Delta y=-d\).

\begin{equation}0=-v_{b}+a_{y, \text { ave }} \Delta t_{\text {col }}\end{equation}

Solving Equation (26.3.15) for the collision time yields

\begin{equation}\Delta t_{\mathrm{col}}=v_{b} / a_{y, \mathrm{ave}}\end{equation}

We can now substitute \(\Delta y=-d\), Equation (26.3.16), and Equation (26.3.11) into Equation (26.3.14) and solve for the y -component of the acceleration, yielding

\begin{equation}a_{y, \text { ave }}=\frac{g h_{0}}{d}\end{equation}

We can solve for the collision time by substituting Equations (26.3.17) and Equation (26.3.11) into Equation (26.3.16) and using the given values in the problem statement, yielding

\begin{equation}\Delta t_{\mathrm{col}}=\frac{2 d}{\sqrt{2 g h_{0}}}=\frac{2\left(1.0 \times 10^{-2} \mathrm{m}\right)}{\sqrt{2\left(9.8 \mathrm{m} \cdot \mathrm{s}^{2}\right)(2.0 \mathrm{m})}}=3.2 \times 10^{-3} \mathrm{s}\end{equation}

Now substitute Equation (26.3.17) for the y -component of the acceleration into Equation (26.3.13) and solve for the average normal force

\begin{equation}N_{\mathrm{ave}}=m g\left(1+\frac{h_{0}}{d}\right)=(60 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)\left(1+\frac{(2.0 \mathrm{m})}{\left(1.0 \times 10^{-2} \mathrm{m}\right)}\right)=1.2 \times 10^{5} \mathrm{N} .(26.3 .19)\end{equation}

Notice that the factor \(1+h_{0} / d \simeq h_{0} / d\) so during the collision we can effectively ignore the external gravitational force. The average compressional force per area on the person’s ankle is the average normal force divided by the cross sectional area

\begin{equation}P=\frac{N_{\text {ave }}}{A} \simeq \frac{m g}{A}\left(\frac{h_{0}}{d}\right)=\frac{1.2 \times 10^{5} \mathrm{N}}{3.2 \times 10^{-4} \mathrm{m}^{2}}=3.7 \times 10^{8} \mathrm{Pa}\end{equation}

From Table 26.3, the tensile strength of the tibia is \(1.4 \times 10^{8} \mathrm{Pa}\), so this fall is enough to break the tibia.

In order to find the minimum displacement that the center of mass must fall in order to avoid breaking the tibia bone, we set the force per area in Equation (26.3.20) equal to \(P=1.4 \times 10^{8} \mathrm{Pa}\). Because at this value of tensile strength,

\begin{equation}\frac{P A}{m g}=\frac{\left(1.4 \times 10^{8} \mathrm{Pa}\right)\left(\left(3.2 \times 10^{-4} \mathrm{m}^{2}\right)\right.}{(60 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)}=80\end{equation}

and so \(P A>>m g\). We can solve Equation (26.3.20) for the minimum displacement

\begin{equation}d_{\min }=\frac{h_{0}}{\left(\frac{P A}{m g}-1\right)} \simeq \frac{m g h_{0}}{P A}=\frac{(60 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(2.0 \mathrm{m})}{\left(1.4 \times 10^{8} \mathrm{Pa}\right)\left(3.2 \times 10^{-4} \mathrm{m}^{2}\right)}=2.6 \mathrm{cm}\end{equation}

where we used the fact that

\begin{equation}\frac{P A}{m g}=\frac{\left(1.4 \times 10^{8} \mathrm{Pa}\right)\left(\left(3.2 \times 10^{-4} \mathrm{m}^{2}\right)\right.}{(60 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)}=76\end{equation}

and so \(P A>>m g\). The ratio

\begin{equation}h_{0} / d_{\min } \simeq P A / m g=76\end{equation}

This ratio depends on the compressive strength of the bone, the cross sectional area, and inversely on the weight of the person. The maximum normal force is anywhere from two to ten times the average normal force. A safe distance to lower the center of mass would be about 20 cm.