27.6: Archimedes’ Principle - Buoyant Force

When we place a piece of solid wood in water, the wood floats on the surface. The density of most woods is less than the density of water, and so the fact that wood floats does not seem so surprising. However, objects like ships constructed from materials like steel that are much denser than water also float. In both cases, when the floating object is at rest, there must be some other force that exactly balances the gravitational force. This balancing of forces also holds true for the fluid itself.

Consider a static fluid with uniform density \( \rho_{f}\). Consider an arbitrary volume element of the fluid with volume V and mass \(m_{f}=\rho_{f} V\). The gravitational force acts on the volume element, pointing downwards, and is given by \(\overrightarrow{\mathbf{F}}^{8}=-\rho_{f} V g \hat{\mathbf{k}}\), where \(\hat{\mathbf{k}}\) is a unit vector pointing in the upward direction. The pressure on the surface is perpendicular to the surface (Figure 27.6). Therefore on each area element of the surface there is a perpendicular force on the surface. The pressure on the surface is perpendicular to the surface (Figure 27.6). Therefore on each area element of the surface there is a perpendicular force on the surface.

Figure 27.6: Forces due to pressure on surface of arbitrary volume fluid element

Figure 27.7: Free-body force diagram on volume element showing gravitational force and buoyant force

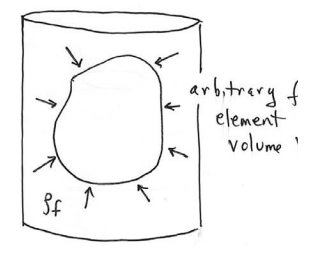
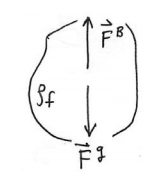
Let \(\overrightarrow{\mathbf{F}}^{B}\) denote the resultant force, called the buoyant force, on the surface of the volume element due to the pressure of the fluid. The buoyant force must exactly balance the gravitational force because the fluid is in static equilibrium (Figure 27.7), \[\overrightarrow{\mathbf{0}}=\overrightarrow{\mathbf{F}}^{B}+\overrightarrow{\mathbf{F}}^{g}=\overrightarrow{\mathbf{F}}^{B}-\rho_{f} V g \hat{\mathbf{k}} \nonumber \] Therefore the buoyant force is therefore \[\overrightarrow{\mathbf{F}}^{B}=\rho_{f} V g \hat{\mathbf{k}} \nonumber \] The buoyant force depends on the density of the fluid, the gravitational constant, and the volume of the fluid element. This macroscopic description of the buoyant force that results from a very large number of collisions of the fluid molecules is called Archimedes’ Principle.

We can now understand why when we place a stone in water it sinks. The density of the stone is greater than the density of the water, and so the buoyant force on the stone is less than the gravitational force on the stone and so it accelerates downward.

Place a uniform object of volume V and mass M with density \(\rho_{o}=M / V\) within a fluid. If the density of the object is less than the density of the fluid, ρ , the object will \(\rho_{o}<\rho_{f}\) float on the surface of the fluid. A portion of the object that is a beneath the surface, displaces a volume \(V_{1}\) of the fluid. The portion of the object that is above the surface displaces a volume \(V_{2}=V-V_{1}\) of air (Figure 27.8).

Figure 27.8: Floating object on surface of fluid

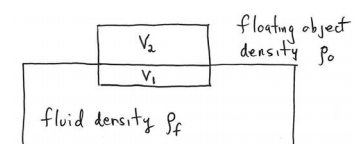
Because the density of the air is much less that the density of the fluid, we can neglect the buoyant force of the air on the object.

Figure 27.9: Free-body force diagram on floating object

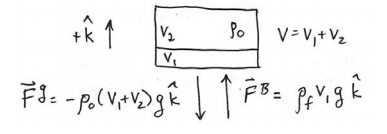
The buoyant force of the fluid on the object, \(\overrightarrow{\mathbf{F}}_{f, o}^{B}=\rho_{f} V_{1} g \hat{\mathbf{k}}\) must exactly balance the gravitational force on the object due to the earth, \(\overrightarrow{\mathbf{F}}_{e, \rho}^{g}\) \[\overrightarrow{\mathbf{0}}=\overrightarrow{\mathbf{F}}_{f, o}^{B}+\overrightarrow{\mathbf{F}}_{e, o}^{g}=\rho_{f} V_{1} g \hat{\mathbf{k}}-\rho_{o} V g \hat{\mathbf{k}}=\rho_{f} V_{1} g \hat{\mathbf{k}}-\rho_{o}\left(V_{1}+V_{2}\right) g \hat{\mathbf{k}} \nonumber \] Therefore the ratio of the volume of the exposed and submerged portions of the object must satisfy \[\rho_{f} V_{1}=\rho_{o}\left(V_{1}+V_{2}\right) \nonumber \] We can solve Eq. (27.6.4) and determine the ratio of the volume of the exposed and submerged portions of the object \[\frac{V_{2}}{V_{1}}=\frac{\left(\rho_{f}-\rho_{o}\right)}{\rho_{o}} \nonumber \] We now also can understand why a ship of mass M floats. The more dense steel displaces a volume of water \(V_{s}\) but a much larger volume of water \(V_{w}\) is displaced by air. The buoyant force on the ship is then \[\overrightarrow{\mathbf{F}}_{s}^{B}=\rho_{f}\left(V_{s}+V_{w}\right) g \hat{\mathbf{k}} \nonumber \] If this force is equal in magnitude to Mg , the ship will float.

Example 27.4 Archimedes' Principle: Floating Wood

Consider a beaker of uniform cross-sectional area A , filled with water of density \(\rho_{w}\). When a rectangular block of wood of cross sectional area \(A_{2}\), height, and mass \(M_{b}\) is placed in the beaker, the bottom of the block is at an unknown depth z below the surface of the water. (a) How far below the surface z is the bottom of the block? (b) How much did the height of the water in the beaker rise when the block was placed in the beaker?

Solution

We neglect the buoyant force due to the displaced air because it is negligibly small compared to the buoyant force due to the water. The beaker, with the floating block of wood, is shown in Figure 27.10.

Figure 27.10 Block of wood floating in a beaker of water

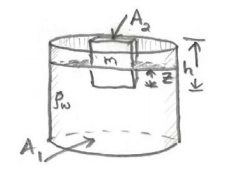
(a) The density of the block of wood is \(\rho_{b}=M_{b} / V_{b}=M_{b} / A_{b} h\) The volume of the submerged portion of the wood is \(V_{1}=A_{b} z\). The volume of the block above the surface is given by \(V_{2}=A_{b}(h-z)\). We can apply Eq. (27.6.5), and determine that \[\frac{V_{2}}{V_{1}}=\frac{A_{b}(h-z)}{A_{b} z}=\frac{(h-z)}{z}=\frac{\left(\rho_{w}-\rho_{b}\right)}{\rho_{b}} \nonumber \] We can now solve Eq. (27.6.7) for the depth z of the bottom of the block \[z=\frac{\rho_{b}}{\rho_{w}} h=\frac{\left(M_{b} / A_{b} h\right)}{\rho_{w}} h=\frac{M_{b}}{\rho_{w} A_{b}} \nonumber \]

(b) Before the block was placed in the beaker, the volume of water in the beaker is \(V_{w}=A s_{i}\), where \(s_{i}\) is the initial height of water in the beaker. When the wood is floating in the beaker, the volume of water in the beaker is equal to \(V_{w}=A s_{f}-A_{b} z\), where \(s_{f}\) is the final height of the water, in the beaker and \(A_{b} z\) is the volume of the submerged portion of block. Because the volume of water has not changed \[A s_{i}=A s_{f}-A_{b} z \nonumber \] We can solve Eq. (27.6.9) for the change in height of the water \(\Delta s=s_{f}-s_{i}\), in terms of i the depth z of the bottom of the block, \[\Delta s=s_{f}-s_{i}=\frac{A_{b}}{A} z \nonumber \] We now substitute Eq. (27.6.8) into Eq. (27.6.10) and determine the change in height of the water \[\Delta s=s_{f}-s_{i}=\frac{M_{b}}{\rho_{w} A} \nonumber \]

Example 27.5 Rock Inside a Floating Salad Bowl

A rock of mass mr and density \(m_{r}\) is placed in a salad bowl of mass \(m_{b}\). The salad bowl and rock float in a beaker of water of density \(\rho_{w}\). The beaker has cross sectional area A. The rock is then removed from the bowl and allowed to sink to the bottom of the beaker. Does the water level rise or fall when the rock is dropped into the water?

Figure 27.11: Rock in a floating salad bowl

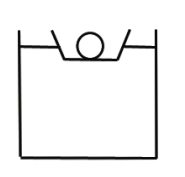
Solution

When the rock is placed in the floating salad bowl, a volume V of water is displaced. The buoyant force \(\overrightarrow{\mathbf{F}}^{B}=\rho_{w} V g \hat{\mathbf{k}}\) balances the gravitational force on the rock and salad bowl, \[\left(m_{r}+m_{b}\right) g=\rho_{w} V g=\rho_{w}\left(V_{1}+V_{2}\right) g \nonumber \] where \(V_{1}\) is the portion of the volume of displaced water that is necessary to balance just the gravitational force on the rock, \(m_{r} g=\rho_{w} V_{1} g\), and \(V_{2}\) is the portion of the volume of displaced water that is necessary to balance just the gravitational force on the bowl, \(m_{b} g=\rho_{w} V_{2} g\), Therefore \(V_{1}\) must satisfy the condition that \(V_{1}=m_{r} g / \rho_{w}\). The volume of the rock is given by \(V_{r}=m_{r} / \rho_{r}\). In particular \[V_{1}=\frac{\rho_{r}}{\rho_{w}} V_{r} \nonumber \] Because the density of the rock is greater than the density of the water, \(\rho_{r}>\rho_{w}\), the rock displaces more water when it is floating than when it is immersed in the water, \(V_{1}>V_{r}\). Therefore the water level drops when the rock is dropped into the water from the salad bowl.

Example 27.6 Block Floating Between Oil and Water

A cubical block of wood, each side of length l = 10 cm , floats at the interface between air and water. The air is then replaced with d = 10 cm of oil that floats on top of the water.

a) Will the block rise or fall? Briefly explain your answer.

After the oil has been added and equilibrium established, the cubical block of wood floats at the interface between oil and water with its lower surface \(h=2.0 \times 10^{-2} \mathrm{m}\) below the interface. The density of the oil is \(\rho_{o}=6.5 \times 10^{2} \mathrm{kg} \cdot \mathrm{m}^{-3}\). The density of water is \(\rho_{w}=1.0 \times 10^{3} \mathrm{kg} \cdot \mathrm{m}^{-3}\).

b) What is the density of the block of wood?

Solution

(a) The buoyant force is equal to the gravitational force on the block. Therefore \[\rho_{b} g V=\rho_{\mathrm{w}} g V_{1}+\rho_{a} g\left(V-V_{1}\right) \nonumber \] where \(V_{1}\) is the volume of water displaced by the block, \(V_{2}=V-V_{1}\) is the volume of air displaced by the block V is the volume of the block, \(\rho_{b}\) is the density of the block of wood, and \(\rho_{a}\) is the density of air (Figure 27.12(a)).

Figure 27.12: (a) Block floating on water, (b) Block floating on oil-water interface

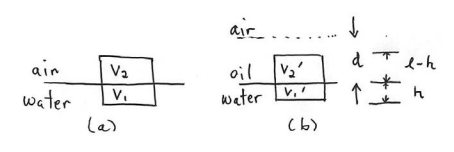
We now solve Eq. (27.6.14) for the volume of water displaced by the block

\[V_{1}=\frac{\left(\rho_{b}-\rho_{a}\right)}{\left(\rho_{w}-\rho_{a}\right)} V \nonumber \] When the oil is added, we can repeat the argument leading up to Eq. (27.6.15) replacing \(\rho_{a}\) with \(\rho_{o}\), (Figure 27.12(b)), yielding

\[\rho_{b} g V=\rho_{w} g V_{1}^{\prime}+\rho_{\sigma} g V_{2}^{\prime} \nonumber \]

where \(V_{1}^{\prime}\) is the volume of water displaced by the block, \(V_{2}^{\prime}\) is the volume of oil displaced by the block, V is the volume of the block, and ρb is the density of the block of wood. Because \(V_{2}^{\prime}=V-V_{1}^{\prime}\), we rewrite Eq. (27.6.16) as

\[\rho_{b} g V=\rho_{\mathrm{w}} g V_{1}^{\prime}+\rho_{o} g\left(V-V_{1}^{\prime}\right) \nonumber \] We now solve Eq. (27.6.17) for the volume of water displaced by the block,

\[V_{1}^{\prime}=\frac{\left(\rho_{b}-\rho_{o}\right) V}{\left(\rho_{w}-\rho_{o}\right)} \nonumber \] Because \(\rho_{o} \gg \rho_{a}\), comparing Equations (27.6.18) and (27.6.15), we conclude that \(V_{1}^{\prime}>V_{1}\). The block rises when the oil is added because more water is displaced.

(b) We use the fact that \(V_{1}^{\prime}=l^{2} h, V_{2}^{\prime}=l^{2}(l-h)\), and \(V=l^{3}\), in Eq. (27.6.16) and solve for the density of the block

\[\rho_{b}=\frac{\rho_{w} V_{1}^{\prime}+\rho_{o} V_{2}^{\prime}}{V}=\frac{\rho_{w} l^{2} h+\rho_{o} l^{2}(l-h)}{l^{3}}=\left(\rho_{w}-\rho_{o}\right) \frac{h}{l}+\rho_{o} \nonumber \]

We now substitute the given values from the problem statement and find that the density of the block is

\[\begin{array}{l}
\rho_{b}=\left(\left(1.0 \times 10^{3} \mathrm{kg} \cdot \mathrm{m}^{-3}\right)-\left(6.5 \times 10^{2} \mathrm{kg} \cdot \mathrm{m}^{-3}\right)\right) \frac{\left(2.0 \times 10^{-2} \mathrm{m}\right)}{\left(1.0 \times 10^{-1} \mathrm{m}\right)}+\left(6.5 \times 10^{2} \mathrm{kg} \cdot \mathrm{m}^{-3}\right) \\
\rho_{b}=7.2 \times 10^{2} \mathrm{kg} \cdot \mathrm{m}^{-3}
\end{array} \nonumber \]

Because \(\rho_{b}>\rho_{o}\), the above analysis is valid.