15.2: Buoyancy
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we examine how the pressure gradient in a fluid leads to a force of buoyancy on an object that is immersed in the fluid.
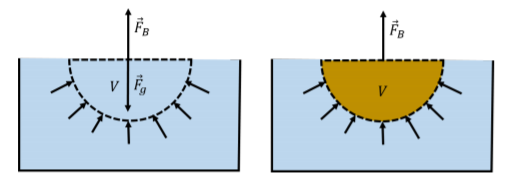
In the left panel of Figure 15.2.1, we show a hemi-spherical element of fluid with a volume V. The weight of the element of fluid, →Fg, is supported by the net upwards force, →FB, exerted by the pressure of the fluid surrounding the fluid element. The mass, M, of the element of fluid is given by:
M=ρV
where ρ is the density of the fluid. The net force from the pressure, FB, must thus have the same magnitude as the weight:
FB+Mg=ρVg
Now, suppose that the fluid element is “displaced” and replaced by the hull of a boat, as shown in the right panel of Figure 15.2.1. The net upwards force from the pressure of the fluid must remain the same, FB, but that force is now exerted on the hull of the boat. We call that force the force of “buoyancy”, which is the reason that a boat can float and the reason that you feel lighter when walking in a swimming pool than on land.
Thus, if an object displaces a volume, V, of a fluid with density ρ, when immersed in the fluid, that object will experience an upwards force of buoyancy, →FB, with magnitude:
FB=ρVg
This “principle” was originally discovered by Archimedes, who stated that the force of buoyancy is equal to the weight of the displaced fluid. Note that we drew the fluid element at the surface of the fluid, but this is not required, and a force of buoyancy will be present if the object is completely immersed in the liquid. If you refer back to Figure 15.2.1, you will recall that the net upwards force on an element of fluid must be equal to its weight, even if the fluid element is completely immersed.
Does the force of buoyancy on a fully submerged object increase with the depth at which the object is submerged (ignoring any change from the varying value of →g)?
- Yes, because the force of buoyancy comes from the pressure in the fluid, which increases with depth.
- No, because the force of buoyancy comes from the difference in pressure above and below the object, which does not increase with depth.
- Answer
- B.
You observe that if you pour olive oil slowly into your glass of water, the oil floats above the water. What can you conclude?
- The mass of a given volume of oil is less than the mass of the same volume of water.
- The mass of a given volume of oil is more than the mass of the same volume of water.
- Answer
- A.
You measure the weight of an object by suspending it with a spring scale. When you measure the weight of the object in air, you find that it has a weight Wa. When you measure the weight of the object when it is completely submerged in water, you find that it has a weight Ww. What is the density of the object?
Solution
Given the weight of the object in air, we can easily determine its mass:
M=Wag
However, since we do not know its volume, V, we cannot directly determine its density. When the object is submerged in water, the measured weight will be the actual weight of the object (as measured in air) minus the magnitude of the force of buoyancy exerted by the water:
Ww=Wa−ρwgV∴
where ρ_{w} is the density of water. Given the volume, we can now determine the object’s density, \rho:
\begin{aligned} \rho = \frac{M}{V}=\frac{W_{a}\rho _{w}g}{g(W_{w}-W_{a})}=\rho _{w}\frac{W_{a}}{W_{w}-W_{a}} \end{aligned}
Discussion
By using Archimedes’ Principle, we were able to determine the volume, and thus the density of the object, by comparing measurements of its weight in air and in water. This is similar to the method that Archimedes came up with to determine if a crown owned by a general was made of real gold or if some of the gold had been replaced with an equal weight of silver. Archimedes supposedly went to the baths to ponder how to determine if the crown was made of gold and had his Eureka moment when we he noticed the water level in the bath went up as he went into the bath. He realized that denser gold would displace less water than silver for an equal weight.
Whether or not an object will float depends on its density. Let’s consider an object that is placed in water. The only forces acting on the object are its weight and the force of buoyancy. We want to know when the net force will be zero. I’m going to write out Newton’s Second Law for the object, but writing the mass of the object in terms of its density and volume.
\begin{aligned} F_{g}&=F_{B} \\[4pt] m_{O}g &=F_{B} \\[4pt] \rho _{O}V_{O}g&=\rho _{W}V_{W}g \end{aligned}
where O refers to the object and W refers to the water. Cancelling out the g’s, we can write this as
\begin{aligned} \frac{\rho _{O}}{\rho _{W}}=\frac{V_{W}}{V_{0}} \end{aligned}
Consider a solid cube that has the same density as water. In this case, ρ_{0}/ρ_{W} = 1, and so V_{W} /V_{0} = 1. This means that, in order for the cube to float, a volume of water that is equal to the volume of the cube must be displaced. So, the entire cube must be submerged. If you placed this cube 5\text{ m} deep in the water, it would stay at this depth.
Now consider a cube whose density is half that of water. We find that ρ_{0}/ρ_{W} = 0.5, so we must have V_{W} /V_{0} = 0.5. In order for the cube to float, only half of it needs to be submerged. If you placed the cube 5\text{ m} deep in the water, it would rise to the surface and stop when half of it was above water (after bobbing for a bit).
Finally, what about a cube whose density is 1.5 times the density of water? In this case, one and a half cubes worth of water would have to be displaced in order for the cube to float. Even when the entire cube is submerged, not enough volume has been displaced in order for it to float, so the cube will sink.
Objects like pool noodles or life jackets allow us to float because they have low densities. They have very little mass (they don’t add much to the weight) in a relatively large volume (they can displace water to add to the buoyant force). An object with a density less than water will float with some fraction of the object being submerged.

