5.4: Oblique Collisions

In Figure V.2 I show two balls just before collision, and just after collision. The horizontal line is the line joining the centres – for short, the "line of centres". We suppose that we know the velocity (speed and direction) of each ball before collision, and the coefficient of restitution. The direction of motion is to be described by the angle that the velocity vector makes with the line of centres. We want to find the velocities (speed and direction) of each ball after collision. That is, we want to find four quantities, and therefore we need four equations. These equations are as follows.

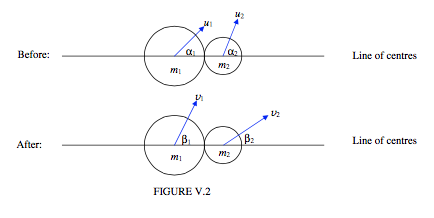
There are no external forces on the system along the line of centres. Therefore the component of momentum of the system along the line of centres is conserved:

$$m_{1}v_{1}\cos\beta_{1} +m_{2}v_{2}\cos \beta_{2} = m_{1}u_{1}\cos \alpha_{1} + m_{2}u_{2}\cos \alpha_{2}. \tag{5.4.1}\label{eq:5.4.1}$$

If we assume that the balls are smooth - i.e. that there are no forces perpendicular to the line of centres and the balls are not set into rotation, then the component of the momentum of each ball separately perpendicular to the line of centres is conserved:

$$v_{1}\sin\beta_{1} = u_{1} \sin \alpha_{1} \tag{5.4.2}\label{eq:5.4.2}$$

and

$$v_{2}\sin\beta_{2} = u_{2} \sin \alpha_{2}. \tag{5.4.3}\label{eq:5.4.3}$$

The last of the four equations is the restitution equation

$$e = \frac{\text{elative speed of recession along the line of centres after collision}}{\text{relative speed of approach along the line of centres before collision}}. \nonumber$$

That is,

$$v_{2}\cos\beta_{2}- v_{1}\cos\beta_{1} =e (u_{1}\cos \alpha_{1}-u_{2}\cos \alpha_{2}). \tag{5.4.4}\label{eq:5.4.4}$$

Example $\PageIndex{1A}$

Suppose $m_{1}$ =3kg, $m_{2}$ = 2kg, $u_{1}$ = 40ms⁻¹ $u_{2}$ = 15ms⁻¹

$\alpha_{1}$ = 10° , $\alpha_{2}$ = 70°, $e$ = 0.8

Find $v_{1}$, $v_{2}$, $\beta_{1}$, $\beta_{2}$.

Solution

$v_{1}$ = 16.28 m s−1 $v_{2}$ = 44.43 m s−1

$\beta_{1}$ = 25°15' $\beta_{2}$ = 18°30'

Example $\PageIndex{1B}$

Suppose $m_{1}$ = 3kg, $m_{2}$ = 3kg, $u_{1}$ = 12ms⁻¹ $u_{2}$ = 15ms⁻¹

$\alpha_{1}$ = 20° , $\alpha_{2}$ = 50°, $\beta_{2}$ = 47°

Find $v_{1}$, $v_{2}$, $\beta_{1}$, $e$.

Solution

$v_{1}$ = 10.50 m s⁻¹ $v_{2}$ = 15.71 m s⁻¹

$\beta_{1}$= 23°00' $e$= 0.6418

Exercise $\PageIndex{1}$

If $u_{2} =0$, and if $e=1$ and if $m_{1} = m_{2}$, show that $\beta_{1}$ = 90° and $\beta_{2}$ = 0°.