17.5: Double Pendulum

This is another similar problem, though, instead of assuming Hooke’s law, we shall assume that angles are small ( $\sin \theta \approx \theta , \cos \theta \approx 1 - \frac{1}{2} \theta^2$ ). For clarity of drawing, however, I have drawn large angles in Figure XVIII.4.

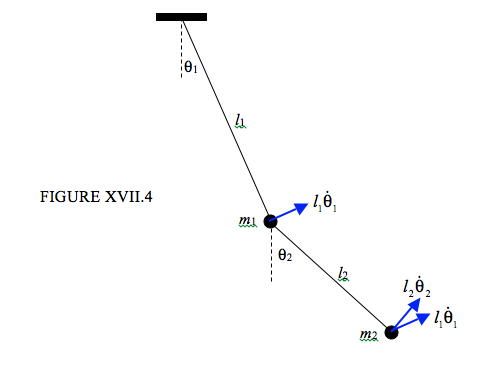
Because I am going to use the lagrangian equations of motion, I have not marked in the forces and accelerations; rather, I have marked in the velocities. I hope that the two components of the velocity of $m_{2}$ that I have marked are self-explanatory; the speed of $m_{2}$ is given by $v^2_{2} = l^2_{1}\dot{\theta}^2_{1} + l^2_{2}\dot{\theta}^2_{2} + 2 l_{1}l_{2}\dot{\theta}_1 \dot{\theta}_2 \cos(\theta_2- \theta_1)$. The kinetic and potential energies are

$$T = \frac{1}{2}m_1l^2_1\dot{\theta}^2_1 + \frac{1}{2}m_1 [l^2_1\dot{\theta}^2_1 + l^2_2\dot{\theta}^2_2 + 2l_1l_2\dot{\theta}_1\dot{\theta}_2 \cos(\theta_2 - \theta_1)], \label{17.5.1}$$

$$V = constant - m_1gl_1 \cos \theta_1 - m_2g(l_1\cos \theta_1 + l_2 \cos \theta_2). \label{17.5.2}$$

If we now make the small angle approximation, these become

$$T = \frac{1}{2} m_1l^2_1 \dot{\theta}^2_1 + \frac{1}{2} m_2(l_1 \dot{\theta}_1 + l_2 \dot{\theta}_2)^2 \label{17.5.3}$$

and

$$V = contant + \frac{1}{2}m_1gl_1\theta^2_1 + \frac{1}{2}m_1g(l_1\theta^2_1 + l_2\theta^2_2) - m_1gl_1 - m_2gl_2. \label{17.5.4}$$

Apply the lagrangian equation in turn to $\theta_1$ and $\theta_2$:

$$(m_1 + m_2)l^2_1\ddot{\theta}_1 + m_2l_1l_2\ddot{\theta} = -(m_1 + m_2)gl_1 \theta_1 \label{17.5.5}$$

and

$$m_2l_1l_2 \ddot{\theta}_1 + m_2l^2_2 \ddot{\theta}_2 = -m_2gl_2\theta_2. \label{17.5.6}$$

Seek solutions in the form of $\dot{\theta}_1 = - \omega \theta_1$ and $\dot{\theta}_2 = - \omega^2 \theta_2$.

Then

$$(m_1 + m_2)(l_2 \omega^2 -g)\theta_1 + m_2l_1l_2 \omega^2 \theta_2 = 0 \label{17.5.7}$$

and

$$l_1 \omega^2\theta_1 + (l_2\omega^2 - g)\theta_2 =0. \label{17.5.8}$$

Either of these gives the displacement ratio $\theta_2/\theta_1$. Equating the two expressions for the ratio $\theta_2/\theta_1$, or putting the determinant of the coefficients to zero, gives the following equation for the frequencies of the normal modes:

$$m_1l_1l_2\omega^4 - (m_1+m_2)g(l_1+l_2)\omega^2 + (m_1+m_2)g^2 = 0. \label{17.5.9}$$

As in the previous examples, there is a slow in-phase mode, and fast out-of-phase mode.

For example, suppose $m_1$ = 0.01 kg, $m_2$ = 0.02 kg, $l_1$ = 0.3 m, $l_2$ = 0.6 m, $g$ = 9.8 m s⁻².

Then $0.0018\omega^4 - 0.02446\omega^2 = 0$. The slow solution is $\omega$ = 3.441 rad s⁻¹ ( $P$ = 1.826 s), and the fast solution is $\omega$ = 11.626 rad s⁻¹ ($P$ =0.540 s). If we put the first of these (the slow solution) in either of equations 17.5.7 or 8 (or both, as a check against mistakes) we obtain the displacement ratio $\theta_2 / \theta_1$ = 1.319, which is an in-phase mode. If we put the second (the fast solution) in either equation, we obtain $\theta_2 / \theta_1$ = −0.5689 , which is an out-of-phase mode. If you were to start with$\theta_2 / \theta_1$ = 1.319 and let go, the pendulum would swing in the slow in-phase mode. If you were to start with $\theta_2 / \theta_1$ = −0.5689 and let go, the pendulum would swing in the fast out-of-phase mode. Otherwise the motion would be a linear combination of the normal modes, with the fraction of each determined by the initial conditions, as in the example in Section 17.3.