24.4: General Motion of a Rotating Rigid Body

We’ll follow the Landau notation (which itself tends to be bilingual between coordinates \((x, y, z) \text { and } \left.\left(x_{1}, x_{2}, x_{3}\right) .\right)\). Notice that we’ll label the components by \(\left(x_{1}, x_{2}, x_{3}\right), \text { not }\left(r_{1}, r_{2}, r_{3}\right)\) even though we call the vector \(\vec{r}\). Again, we’re following Landau.

We take a fixed, inertial (or lab) coordinate system labeled \((X,Y,Z)\) and in this system the rigid body’s center of mass, labeled \(O\), is at \(\vec{R}\). We have a Cartesian set of axes fixed in the body, origin at the center of mass, and coordinates in this system, vectors from \(O\)  to a point in the body denoted by \(\vec{r}\) are labeled \((x,y,z)\) or \(\left(x_{1}, x_{2}, x_{3}\right)\).

A vector from the external inertial fixed origin to a point in the body is then

\(\vec{R}+\vec{r}=\vec{\rho}\)

say, as shown in the figure.

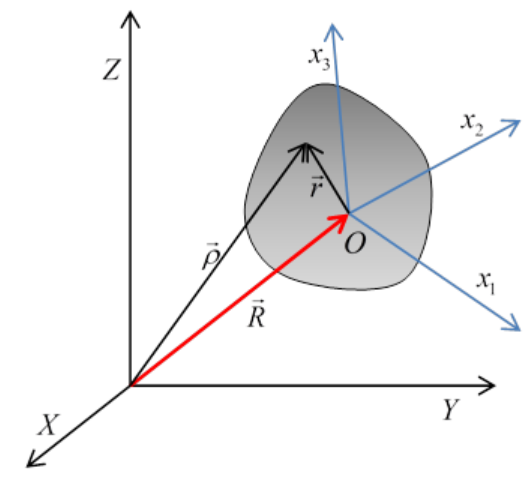
Suppose now that in infinitesimal time \(dt\), the center of mass of the body moves \(d \vec{R}\) and the body rotates through \(d \vec{\phi}\). Then a particle at \(\vec{r}\) as measured from the center of mass will move through

\(d \vec{\rho}=d \vec{R}+d \vec{\phi} \times \vec{r}\)

Therefore, the velocity of that particle in the fixed frame, writing the center of mass velocity and the angular velocity as

\(d \vec{R} / d t=\vec{V}, \quad d \vec{\phi} / d t=\vec{\Omega}\)

is

\(\vec{v}=\vec{V}+\vec{\Omega} \times \vec{r}\)

Now, in deriving the above equation, we have not used the fact that the origin \(O\) fixed in the body is at the center of mass. (That turns out to be useful shortly.) What if instead we had taken some other origin \(O^{\prime}\) fixed in the body? Would we find the angular velocity \(\overrightarrow{\Omega^{\prime}} \text { about } O^{\prime} \text { to be the same as } \vec{\Omega}\)? The answer turns out to be yes, but we need to prove it! Here's the proof:

If the position of \(O^{\prime} \text { relative to } O \text { is } \vec{a} \text { (a vector fixed in the body and so moving with it) then the velocity } \overrightarrow{V^{\prime}} \text { of } O^{\prime}\) is

\(\overrightarrow{V^{\prime}}=\vec{V}+\vec{\Omega} \times \vec{a}\)

A particle at \(\vec{r} \text { relative to } O \text { is at } \overrightarrow{r^{\prime}}=\vec{r}-\vec{a} \text { relative to } O^{\prime}\)

Its velocity relative to the fixed external axes is

\begin{equation}
\vec{v}=\overrightarrow{V^{\prime}}+\overrightarrow{\Omega^{\prime}} \times \overrightarrow{r^{\prime}}
\end{equation}

this must of course equal

\begin{equation}
\vec{V}+\vec{\Omega} \times \vec{r}=\vec{V}+\vec{\Omega} \times \overrightarrow{r^{\prime}}+\vec{\Omega} \times \vec{a}=\vec{V}^{\prime}+\vec{\Omega} \times \overrightarrow{r^{\prime}}
\end{equation}

It follows that \(\overrightarrow{\Omega^{\prime}}=\vec{\Omega}\)

This means that if we describe the motion of any particle in the body in terms of some origin fixed in the body, plus rotation about that origin, the angular velocity vector describing the body’s motion is the same irrespective of the origin we choose. So we can, without ambiguity, talk about the angular velocity of the body.

From now on, we’ll assume that the origin fixed in the body is at the center of mass.