26.2: Precession of a Symmetrical Top

Last updated
Save as PDF

Page ID: 30538

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

A more interesting case is the free rotation (zero external torque) of a symmetrical top, meaning \(I_{1}=I_{2} \neq I_{3}\).

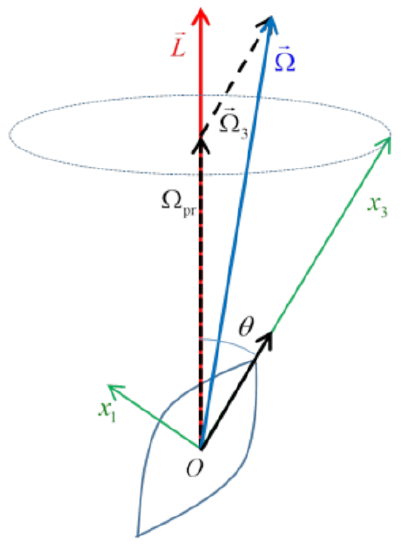
We can take any pair of orthogonal axes, perpendicular to the body’s symmetry axis, as the \(x_{1}, x_{2}\) axes. We’ll choose \(x_{2}\) following Landau, as perpendicular to the plane containing \(\vec{L}\) and the momentary position of the \(x_{3}\) axis, so in the diagram here \(x_{2}\) is perpendicularly out from the paper/screen, towards the viewer.

This means the angular momentum component \(L_{2}=0\) and therefore \(\Omega_{2}=0 . \text { Hence } \vec{\Omega}\) is in the same plane as \(\vec{L}, x_{3}, \text { and so the velocity } \vec{v}=\vec{\Omega} \times \vec{r}\) of every point on the axis of the top is perpendicular to this plane (into the paper/screen). The axis of the top \(O x_{3}\) must be rotating uniformly about the direction of \(\vec{L}\).

The spin rate of the top around its own axis is

\begin{equation}
\Omega_{3}=L_{3} / I_{3}=\left(L / I_{3}\right) \cos \theta
\end{equation}

The angular velocity vector \(\vec{\Omega}\) can be written as a sum of two components, one along the body’s axis \(O x_{3}\) and one parallel to the angular momentum \(\vec{L}\) (these components are shown dashed in the figure)

\begin{equation}
\vec{\Omega}=\vec{\Omega}_{\text {precession }}+\vec{\Omega}_{3}
\end{equation}

The component along the body’s axis \(O x_{3}\) does not contribute to the precession, which all comes from the component along the (fixed in space) angular momentum vector.

The speed of precession follows from

\begin{equation}
\Omega_{\text {precession }} \sin \theta=\Omega_{1}
\end{equation}

and

\begin{equation}
\Omega_{1}=L_{1} / I_{1}=\left(L / I_{1}\right) \sin \theta
\end{equation}

\begin{equation}
\Omega_{\text {precession }}=L / I_{1}
\end{equation}

Note also the ratio of precession rate to spin around axis is

\begin{equation}
\Omega_{\text {precession }} / \Omega_{3}=\left(I_{3} / I_{1}\right) \sec \theta
\end{equation}

This means the precession rate and the spin are very comparable, except when \(\theta\) is near \(\pi / 2\), when the precession becomes much faster. Remember this is the body’s precession with no external torque, and is clearly completely different—much faster precession—than the familiar case of a fast spinning top under gravity.