1.7: Stokes’ Law
( \newcommand{\kernel}{\mathrm{null}\,}\)
Dropping the Ball (Slowly)
We’ve seen how viscosity acts as a frictional brake on the rate at which water flows through a pipe, let us now examine its frictional effect on an object falling through a viscous medium. To make it simple, we take a sphere. If we use a very viscous liquid, such as glycerin, and a small sphere, for example a ball bearing of radius a millimeter or so, it turns out experimentally that the liquid flows smoothly around the ball as it falls, with a flow pattern like:
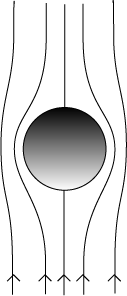
If we knew mathematically precisely how the velocity in this flow pattern varied near the ball, we could find the total viscous force on the ball by finding the velocity gradient near each little area of the ball’s surface, and doing an integral. But actually this is quite difficult. It was done in the 1840’s by Sir George Gabriel Stokes. He found what has become known as Stokes’ Law: the drag force F on a sphere of radius a moving through a fluid of viscosity η at speed v is given by:
F=6πaηv
This drag force is directly proportional to the radius. That’s not obvious—one might have thought it would be proportional to the cross-section area, which would go as the square of the radius. The drag force is also directly proportional to the speed, not, for example to v2.
Understanding Stokes’ Law with Dimensional Analysis
Is there some way we could see the drag force must be proportional to the radius, and to the speed, without wading through all of Sir George’s mathematics? The answer is yes—by using dimensions.
- First we must ask: what can this drag force depend on? Obviously, it depends on the size of the ball: let’s say the radius is a, having dimension L.
- It must depend on the speed v, which has dimension LT−1
- Finally, it depends on the coefficient of viscosity η which has dimensions ML−1T−1.
The drag force F has dimensions [F]=MLT−2 what combination of [α]=L,[ν]=LT−1 and [η]=ML−1T−1 will give [F]=MLT−2?
It’s easy to see immediately that F must depend linearly on η, that’s the only way to balance the M term. Now let’s look at Fη, which can only depend on a and v.
[Fη]=L2T−1.
The only possible way to get a function of a, v having dimension L2T−1 is to take the product av.
So, the dimensional analysis establishes that the drag force is given by:
F=Cαην
where C is a constant that cannot be determined by dimensional considerations.
Experimental Check
We can check this result by dropping small steel balls through glycerin. We choose glycerin because it has a very high viscosity, so the balls fall slowly enough for us to be able to time them (Figure 1.7.2.

One problem is that the viscosity of glycerin is very temperature dependent, being 1.49 Pa.sec at 20o C, and 0.95 Pa.sec at 25oC. We measured the temperature of our glycerin to be 23oC, so we assumed its viscosity was 1.17 Pa.sec., just taking a linear interpolation. We used a ball of radius 1.2mm, weighing 0.05 grams. On dropping it through the glycerin, and allowing some distance for it to reach a steady speed, we found it fell 25 cm. in 11.1 seconds, a speed of 0.022 m sec-1. So the drag force should be:
F=6παην≈18.8×1.2×10−3×1.17×2.2×10−2≈6×10−4N
If the ball is dropping at a steady speed, this force should just balance the weight of the ball. The mass is 0.05grams, which is 5.10-4 N. But we should also have subtracted off a buoyancy force, which would get this closer to 4.10-4 N. Since we think our measurements of radius, mass and speed were fairly accurate, the viscosity was evidently less than we thought. Bearing in mind that it drops by 10% for each one-degree rise in temperature, most likely it was not at a uniform temperature, or our measurement of temperature was inaccurate.
We checked the dimensional prediction by dropping a ball of exactly twice the radius. It fell in exactly one-quarter of the time. This confirms the correctness of the dimensional analysis, because once the ball has reached terminal velocity vterm, and therefore is no longer accelerating, it must feel zero net force. At this stage, the forces of viscous drag and weight must be in balance:
Cαηνterm=(43)πα3ρg.
It follows that for two balls of the same density ρ, after canceling a from each side, the ratio of their terminal velocities is the square of the ratio of their radii, a ball with radius 2a will fall four times faster than a ball with radius a. This is what we found experimentally.
Example 1.7.1
Assuming the flow pattern in the diagram above has the same proportions for different radii (so for a larger radius ball it’s the same pattern magnified), how does the fluid velocity gradient near the “equator” of the ball change on going from a ball of radius a to one of radius 2a? (Assume the two balls are falling through the fluid at the same speed.) Argue that most of the viscous drag on the sphere takes place in a band surrounding the equator (so, a band shaped like the tropical zone on the earth). From this, make plausible that the total viscous drag will be proportional to the sphere’s radius, not to the square of the radius.
Contributors
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)


