8.1: Conservative Forces
- Page ID
- 19412
In Chapter 7, we introduced the concept of work, \(W\), done by a force, \(\vec F(\vec r)\), acting on an object as it moves along a path from position \(A\) to position \(B\):
\[W=\int_{A}^{B} \vec F (\vec r)\cdot d\vec l\]
where \(\vec F(\vec r)\) is a force vector that, in general, is different at different positions in space (\(\vec r\)). We can also say that \(\vec F\) depends on position by writing \(\vec F(\vec r)=\vec F(x,y,z)\), since the position vector, \(\vec r\), is simply the vector \(\vec r = x\hat x + y \hat y+ z\hat z\). That is, \(\vec F(\vec r)\) is just a short hand notation for \(\vec F(x,y,z)\), and \(d\vec l\) is a (very) small segment along the particular path over which one calculates the work.
The above integral is, in general, difficult to evaluate, as it depends on the specific path over which the object moved. In Example 7.1.2 of Chapter 7, we calculated the work done by friction on a crate that was slid across the floor along two different paths and indeed found that the work depended on the path that was taken. In Example 7.1.3 of the same chapter, we saw that the work done by the force of gravity when moving a box along two different paths did not depend on the path chosen1.
We call “conservative forces” those forces for which the work done only depends on the initial and final positions and not on the path taken between those two positions. “Non-conservative” forces are those for which the work done does depend on the path taken. The force of gravity is an example of a conservative force, whereas friction is an example of a non-conservative force.
This means that the work done by a conservative force on a “closed path” is zero; that is, the work done by a conservative force on an object is zero if the object moves along a path that brings it back to its starting position. Indeed, since the work done by a conservative force only depends on the location of the initial and final positions, and not the path taken between them, the work has to be zero if the object ends in the same place as where it started (a possible path is for the object to not move at all).
Consider the work done by gravity in raising (displacement \(\vec d_1\)) and lowering (displacement \(\vec d_2=-\vec d_1\)) an object back to its starting position along a vertical path, as depicted in Figure \(\PageIndex{1}\).
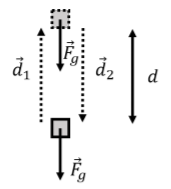
The total work done by gravity on this particular closed path is easily shown to be zero, as the work can be broken up into the negative work done as the object moves up (displacement vector \(\vec d_1\)) and the positive work done as the object moves down (displacement vector \(\vec d_2\)):
\[\begin{aligned} W^{tot} = \vec F_g \cdot \vec d_1 + \vec F_g \cdot \vec d_2 = -mgd + mgd = 0 \end{aligned}\]
In order to write the path integral of the force over a closed path, we introduce a new notation to indicate that the starting and ending position are the same:
\[\begin{aligned} \int_A^A \vec F(\vec r) \cdot d\vec l = \oint \vec F(\vec r) \cdot d\vec l\end{aligned}\]
The condition for a force to be conservative is thus:
\[\oint \vec F(\vec r) \cdot d\vec \ =0\]
since this means that the work done over a closed path is zero. The condition for this integral to be zero can be found by Stokes’ Theorem:
\[\begin{aligned} \oint \vec F(\vec r) \cdot d\vec l = \int_S \left[\left(\frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z}\right)\hat x+ \left(\frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x}\right)\hat y + \left(\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}\right)\hat z \right]\cdot d\vec A\end{aligned}\]
where the integral on the right is called a “surface integral” over the surface, \(S\), enclosed by the closed path over which the work is being calculated. Don’t worry, it is way beyond the scope of this text to understand this integral or Stokes’ Theorem in detail! It is however useful in that it gives us the following conditions on the components of a force for that force to be conservative (by requiring the terms in parentheses to be zero):
\[\frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z}=0\]
\[\frac{\partial F_{x}}{\partial x}-\frac{\partial F_{z}}{\partial x}=0\]
\[\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}=0\]
In general:
- A force can be conservative if it only depends on position in space, and not speed, time, or any other quantity.
- A force is conservative if it is constant in magnitude and direction.
You push a crate from point \(A\) to point \(B\) along a horizontal surface. Is the force you exert a conservative force?
- Yes
- No
- Not enough information
- Answer
- C.
Is the force of gravity on an object of mass \(m\), near the surface of the Earth, given by:
\[\begin{aligned} \vec F(x,y,z) =0\hat x + 0\hat y -mg \hat z\end{aligned}\]
conservative? Note that we have defined the \(z\) axis to be vertical and positive upwards.
Solution
The force is expected to be conservative since it is constant in magnitude and direction. We can verify this using the conditions in Equation 8.1.3, 8.1.4, and 8.1.5:
\[\begin{aligned} \frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z} &= \frac{\partial}{\partial y}(-mg) - 0 &= 0\\[4pt] \frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x} &= 0 - \frac{\partial}{\partial x}(-mg) &= 0\\[4pt] \frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y} &= 0 - 0 &=0\end{aligned}\]
and the force is indeed conservative since all three conditions are zero.
Is the following force conservative?
\[\begin{aligned} \vec F(x,y,z) = \frac{-k}{r^3}\vec r = \frac{-kx}{(x^2+y^2+z^2)^\frac{3}{2}}\hat x + \frac{-ky}{(x^2+y^2+z^2)^\frac{3}{2}}\hat y + \frac{-kz}{(x^2+y^2+z^2)^\frac{3}{2}}\hat z\end{aligned}\]
Solution
Since the force only depends on position, it could be conservative, so we must check using the conditions from Equations 8.1.3, 8.1.4, and 8.1.5:
\[\begin{aligned} \frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z} &= \frac{\partial }{\partial y}\left(\frac{-kz}{(x^2+y^2+z^2)^\frac{3}{2}}\right)-\frac{\partial}{\partial z}\left( \frac{-ky}{(x^2+y^2+z^2)^\frac{3}{2}}\right)\\[4pt] &=\frac{3kz(2y)}{2(x^2+y^2+z^2)^\frac{5}{2}}-\frac{3ky(2z)}{2(x^2+y^2+z^2)^\frac{5}{2}} = 0\\[4pt] \frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x} &= \frac{\partial}{\partial z}\left(\frac{-kx}{(x^2+y^2+z^2)^\frac{3}{2}}\right)-\frac{\partial}{\partial x}\left( \frac{-kz}{(x^2+y^2+z^2)^\frac{3}{2}}\right)\\[4pt] &=\frac{3kx(2z)}{2(x^2+y^2+z^2)^\frac{5}{2}}-\frac{3kz(2x)}{2(x^2+y^2+z^2)^\frac{5}{2}} = 0\\[4pt] \frac{\partial F_y}{\partial x}-\frac{\partial F_{x}}{\partial y} &= \frac{\partial}{\partial x}\left(\frac{-ky}{(x^2+y^2+z^2)^\frac{3}{2}}\right)-\frac{\partial}{\partial y}\left( \frac{-kx}{(x^2+y^2+z^2)^\frac{3}{2}}\right)\\[4pt] &=\frac{3ky(2x)}{2(x^2+y^2+z^2)^\frac{5}{2}}-\frac{3kx(2y)}{2(x^2+y^2+z^2)^\frac{5}{2}} = 0\end{aligned}\]
where we used the Chain Rule to take the derivatives. Since all of the conditions are zero, the force is conservative. As we will see, the force represented here is similar mathematically to both the force that Newton introduced in his Universal Theory of Gravity, and the force introduced by Coulomb as the electric force, which are both conservative.
Footnotes
1. At least for those two paths that we tried in the example.

