3.7: Problems
- Page ID
- 1004
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. Experiments show that the power consumed by a boat's engine is approximately proportional to the third power of its speed. (We assume that it is moving at constant speed.)
(a) When a boat is cruising at constant speed, what type of energy transformation do you think is being performed?
(b) If you upgrade to a motor with double the power, by what factor is your boat's maximum cruising speed increased? (solution in the pdf version of the book)
2. Object A has a kinetic energy of 13.4 J. Object B has a mass that is greater by a factor of 3.77, but is moving more slowly by a factor of 2.34. What is object B's kinetic energy? (solution in the pdf version of the book)
3. My 1.25 kW microwave oven takes 126 seconds to bring 250 g of water from room temperature to a boil. What percentage of the power is being wasted? Where might the rest of the energy be going? (solution in the pdf version of the book)
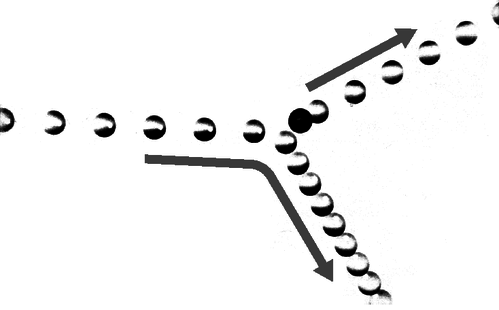
a / Problem 4.
4. The multiflash photograph shows a collision between two pool balls. The ball that was initially at rest shows up as a dark image in its initial position, because its image was exposed several times before it was struck and began moving. By making measurements on the figure, determine numerically whether or not energy appears to have been conserved in the collision. What systematic effects would limit the accuracy of your test? [From an example in PSSC Physics.]
5. A grasshopper with a mass of 110 mg falls from rest from a height of 310 cm. On the way down, it dissipates 1.1 mJ of heat due to air resistance. At what speed, in m/s, does it hit the ground? (solution in the pdf version of the book)
6. A ball rolls up a ramp, turns around, and comes back down. When does it have the greatest gravitational energy? The greatest kinetic energy? [Based on a problem by Serway and Faughn.]
7. (a) You release a magnet on a tabletop near a big piece of iron, and the magnet leaps across the table to the iron. Does the magnetic energy increase, or decrease? Explain. (b) Suppose instead that you have two repelling magnets. You give them an initial push towards each other, so they decelerate while approaching each other. Does the magnetic energy increase, or decrease? Explain.
8. Estimate the kinetic energy of an Olympic sprinter.
9. (answer check available at lightandmatter.com) You are driving your car, and you hit a brick wall head on, at full speed. The car has a mass of 1500 kg. The kinetic energy released is a measure of how much destruction will be done to the car and to your body. Calculate the energy released if you are traveling at (a) 40 mi/hr, and again (b) if you're going 80 mi/hr. What is counterintuitive about this, and what implication does this have for driving at high speeds?
10. A closed system can be a bad thing --- for an astronaut sealed inside a space suit, getting rid of body heat can be difficult. Suppose a 60-kg astronaut is performing vigorous physical activity, expending 200 W of power. If none of the heat can escape from her space suit, how long will it take before her body temperature rises by 6°{}C (11°{}F), an amount sufficient to kill her? Assume that the amount of heat required to raise her body temperature by 1°{}C is the same as it would be for an equal mass of water. Express your answer in units of minutes. (answer check available at lightandmatter.com)
11. The following table gives the amount of energy required in order to heat, melt, or boil a gram of water.
| heat 1 g of ice by 1°C | 2.05 J |
| melt 1 g of ice | 333 J |
| heat 1 g of liquid by 1°C | 4.19 J |
| boil 1 g of water | 2500 J |
| heat 1 g of steam by 1°C | 2.01 J |
(a) How much energy is required in order to convert 1.00 g of ice at -20 \(°\text{C}\) into steam at 137 \(°\text{C}\)? (answer check available at lightandmatter.com)
(b) What is the minimum amount of hot water that could melt 1.00 g of ice? (answer check available at lightandmatter.com)
12. Anya climbs to the top of a tree, while Ivan climbs half-way to the top. They both drop pennies to the ground. Compare the kinetic energies and velocities of the pennies on impact, using ratios.
13. Anya and Ivan lean over a balcony side by side. Anya throws a penny downward with an initial speed of 5 m/s. Ivan throws a penny upward with the same speed. Both pennies end up on the ground below. Compare their kinetic energies and velocities on impact.
14. (a) A circular hoop of mass \(m\) and radius \(r\) spins like a wheel while its center remains at rest. Let \(\omega\) (Greek letter omega) be the number of radians it covers per unit time, i.e., \(\omega=2\pi/T\), where the period, \(T\), is the time for one revolution. Show that its kinetic energy equals \((1/2)m\omega^2r^2\).
(b) Show that the answer to part a has the right units. (Note that radians aren't really units, since the definition of a radian is a unitless ratio of two lengths.)
(c) If such a hoop rolls with its center moving at velocity \(v\), its kinetic energy equals \((1/2)mv^2\), plus the amount of kinetic energy found in part a. Show that a hoop rolls down an inclined plane with half the acceleration that a frictionless sliding block would have.
15. On page 83, I used the chain rule to prove that the acceleration of a free-falling object is given by \(a=-g\). In this problem, you'll use a different technique to prove the same thing. Assume that the acceleration is a constant, \(a\), and then integrate to find \(v\) and \(y\), including appropriate constants of integration. Plug your expressions for \(v\) and \(y\) into the equation for the total energy, and show that \(a=-g\) is the only value that results in constant energy.
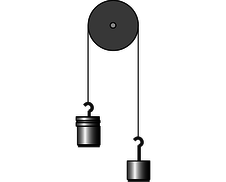
b / Problem 16.
16. The figure shows two unequal masses, \(m_1\) and \(m_2\), connected by a string running over a pulley. Find the acceleration. \hwhint{hwhint:atwood-energy-sn}(answer check available at lightandmatter.com)
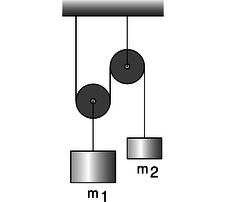
c / Problem 17.
17. What ratio of masses will balance the pulley system shown in the figure? \hwhint{hwhint:pulley}
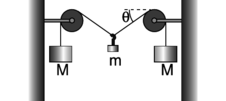
d / Problem 18.
18. (a) For the apparatus shown in the figure, find the equilibrium angle \(\theta\) in terms of the two masses.(answer check available at lightandmatter.com)
(b) Interpret your result in the case of \(M\gg m\) (\(M\) much greater than \(m\)). Does it make sense physically?
(c) For what combinations of masses would your result give nonsense? Interpret this physically. \hwhint{hwhint:tightropish}
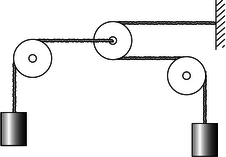
e / Problem 19.
19. In the system shown in the figure, the pulleys on the left and right are fixed, but the pulley in the center can move to the left or right. The two hanging masses are identical, and the pulleys and ropes are all massless. Find the upward acceleration of the mass on the left, in terms of \(g\) only. \hwhint{hwhint:funkyatwood}(answer check available at lightandmatter.com)
20. Two atoms will interact via electrical forces between their protons and electrons. One fairly good approximation to the electrical energy is the Lennard-Jones formula,
\[\begin{equation*} U (r) = k\left[\left(\frac{a}{r}\right)^{12}-2\left(\frac{a}{r}\right)^{6}\right], \end{equation*}\]
where \(r\) is the center-to-center distance between the atoms and \(k\) is a positive constant. Show that (a) there is an equilibrium point at \(r=a\),
(b) the equilibrium is stable, and
(c) the energy required to bring the atoms from their equilibrium separation to infinity is \(k\). \hwhint{hwhint:lennardjones}
21. The International Space Station orbits at an altitude of about 360 to 400 km. What is the gravitational field of the earth at this altitude?(answer check available at lightandmatter.com)
22. (a) A geosynchronous orbit is one in which the satellite orbits above the equator, and has an orbital period of 24 hours, so that it is always above the same point on the spinning earth. Calculate the altitude of such a satellite.(answer check available at lightandmatter.com)
(b) What is the gravitational field experienced by the satellite? Give your answer as a percentage in relation to the gravitational field at the earth's surface.\hwhint{hwhint:geosynch}(answer check available at lightandmatter.com)
23. Astronomers calculating orbits of planets often work in a nonmetric system of units, in which the unit of time is the year, the unit of mass is the sun's mass, and the unit of distance is the astronomical unit (A.U.), defined as half the long axis of the earth's orbit. In these units, find an exact expression for the gravitational constant, \(G\).(answer check available at lightandmatter.com)
24. The star Lalande 21185 was found in 1996 to have two planets in roughly circular orbits, with periods of 6 and 30 years. What is the ratio of the two planets' orbital radii?(answer check available at lightandmatter.com)
25. A projectile is moving directly away from a planet of mass \(M\) at exactly escape velocity. (a) Find \(r\), the distance from the projectile to the center of the planet, as a function of time, \(t\), and also find \(v(t)\).(answer check available at lightandmatter.com)
(b) Check the units of your answer.
(c) Does \(v\) show the correct behavior as \(t\) approaches infinity? \hwhint{hwhint:escape2}
26. The purpose of this problem is to estimate the height of the tides. The main reason for the tides is the moon's gravity, and we'll neglect the effect of the sun. Also, real tides are heavily influenced by landforms that channel the flow of water, but we'll think of the earth as if it was completely covered with oceans. Under these assumptions, the ocean surface should be a surface of constant \(U/m\). That is, a thimbleful of water, \(m\), should not be able to gain or lose any gravitational energy by moving from one point on the ocean surface to another. If only the spherical earth's gravity was present, then we'd have \(U/m=-GM_e/r\), and a surface of constant \(U/m\) would be a surface of constant \(r\), i.e., the ocean's surface would be spherical. Taking into account the moon's gravity, the main effect is to shift the center of the sphere, but the sphere also becomes slightly distorted into an approximately ellipsoidal shape. (The shift of the center is not physically related to the tides, since the solid part of the earth tends to be centered within the oceans; really, this effect has to do with the motion of the whole earth through space, and the way that it wobbles due to the moon's gravity.) Determine the amount by which the long axis of the ellipsoid exceeds the short axis. \hwhint{hwhint:tides}
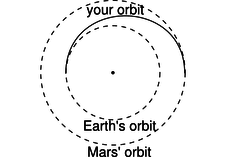
f / Problem 27.
27. You are considering going on a space voyage to Mars, in which your route would be half an ellipse, tangent to the Earth's orbit at one end and tangent to Mars' orbit at the other. Your spacecraft's engines will only be used at the beginning and end, not during the voyage. How long would the outward leg of your trip last? (The orbits of Earth and Mars are nearly circular, and Mars's is bigger by a factor of 1.52.) (answer check available at lightandmatter.com)
28. When you buy a helium-filled balloon, the seller has to inflate it from a large metal cylinder of the compressed gas. The helium inside the cylinder has energy, as can be demonstrated for example by releasing a little of it into the air: you hear a hissing sound, and that sound energy must have come from somewhere. The total amount of energy in the cylinder is very large, and if the valve is inadvertently damaged or broken off, the cylinder can behave like bomb or a rocket.
Suppose the company that puts the gas in the cylinders prepares cylinder A with half the normal amount of pure helium, and cylinder B with the normal amount. Cylinder B has twice as much energy, and yet the temperatures of both cylinders are the same. Explain, at the atomic level, what form of energy is involved, and why cylinder B has twice as much.
29. Explain in terms of conservation of energy why sweating cools your body, even though the sweat is at the same temperature as your body. Describe the forms of energy involved in this energy transformation. Why don't you get the same cooling effect if you wipe the sweat off with a towel? Hint: The sweat is evaporating.
31. All stars, including our sun, show variations in their light output to some degree. Some stars vary their brightness by a factor of two or even more, but our sun has remained relatively steady during the hundred years or so that accurate data have been collected. Nevertheless, it is possible that climate variations such as ice ages are related to long-term irregularities in the sun's light output. If the sun was to increase its light output even slightly, it could melt enough Antarctic ice to flood all the world's coastal cities. The total sunlight that falls on Antarctica amounts to about \(1\times10^{16}\) watts. In the absence of natural or human-caused climate change, this heat input to the poles is balanced by the loss of heat via winds, ocean currents, and emission of infrared light, so that there is no net melting or freezing of ice at the poles from year to year. Suppose that the sun changes its light output by some small percentage, but there is no change in the rate of heat loss by the polar caps. Estimate the percentage by which the sun's light output would have to increase in order to melt enough ice to raise the level of the oceans by 10 meters over a period of 10 years. (This would be enough to flood New York, London, and many other cities.) Melting 1 kg of ice requires \(3\times10^3\) J.
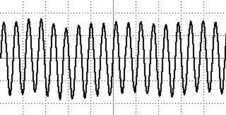
g / Problem 32.
32. The figure shows the oscillation of a microphone in response to the author whistling the musical note “A.” The horizontal axis, representing time, has a scale of 1.0 ms per square. Find the period \(T\), the frequency \(f\), and the angular frequency \(\omega\).(answer check available at lightandmatter.com)
33. (a) A mass \(m\) is hung from a spring whose spring constant is \(k\). Write down an expression for the total interaction energy of the system, \(U\), and find its equilibrium position.\hwhint{hwhint:hangfromspring}
(b) Explain how you could use your result from part a to determine an unknown spring constant.
34. A certain mass, when hung from a certain spring, causes the spring to stretch by an amount \(h\) compared to its equilibrium length. If the mass is displaced vertically from this equilibrium, it will oscillate up and down with a period \(T_{osc}\). Give a numerical comparison between \(T_{osc}\) and \(T_{fall}\), the time required for the mass to fall from rest through a height \(h\), when it isn't attached to the spring. (You will need the result of problem 33).(answer check available at lightandmatter.com)
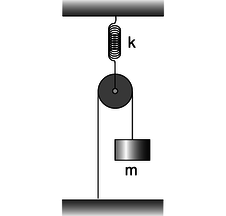
h / Problem 35.
35. Find the period of vertical oscillations of the mass \(m\). The spring, pulley, and ropes have negligible mass.\hwhint{hwhint:pulleyandspring}(answer check available at lightandmatter.com)
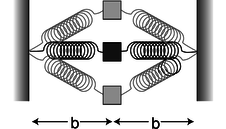
i / Problem 36.
36. The equilibrium length of each spring in the figure is \(b\), so when the mass \(m\) is at the center, neither spring exerts any force on it. When the mass is displaced to the side, the springs stretch; their spring constants are both \(k\).
(a) Find the energy, \(U\), stored in the springs, as a function of \(y\), the distance of the mass up or down from the center.(answer check available at lightandmatter.com)
(b) Show that the period of small up-down oscillations is infinite.
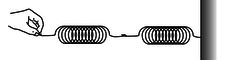
j / Problem 37.
37. Two springs with spring constants \(k_1\) and \(k_2\) are put together end-to-end. Let \(x_1\) be the amount by which the first spring is stretched relative to its equilibrium length, and similarly for \(x_2\). If the combined double spring is stretched by an amount \(b\) relative to its equilibrium length, then \(b=x_1+x_2\). Find the spring constant, \(K\), of the combined spring in terms of \(k_1\) and \(k_2\). \hwhint{hwhint:springsseries}\hwans{hwans:springsseries} (answer check available at lightandmatter.com)
38. A mass \(m\) on a spring oscillates around an equilibrium at \(x=0\). Any function \(U(x)\) with an equilibrium at \(x=0\) can be approximated as \(U(x)=(1/2)kx^2\), and if the energy is symmetric with respect to positive and negative values of \(x\), then the next level of improvement in such an approximation would be \(U(x)=(1/2)kx^2+bx^4\). The general idea here is that any smooth function can be approximated locally by a polynomial, and if you want a better approximation, you can use a polynomial with more terms in it. When you ask your calculator to calculate a function like \(\sin\) or \(e^x\), it's using a polynomial approximation with 10 or 12 terms. Physically, a spring with a positive value of \(b\) gets stiffer when stretched strongly than an “ideal” spring with \(b=0\). A spring with a negative \(b\) is like a person who cracks under stress --- when you stretch it too much, it becomes more elastic than an ideal spring would. We should not expect any spring to give totally ideal behavior no matter no matter how much it is stretched. For example, there has to be some point at which it breaks.
Do a numerical simulation of the oscillation of a mass on a spring whose energy has a nonvanishing \(b\). Is the period still independent of amplitude? Is the amplitude-independent equation for the period still approximately valid for small enough amplitudes? Does the addition of a positive \(x^4\) term tend to increase the period, or decrease it? Include a printout of your program and its output with your homework paper.
39. An idealized pendulum consists of a pointlike mass \(m\) on the end of a massless, rigid rod of length \(L\). Its amplitude, \(\theta\), is the angle the rod makes with the vertical when the pendulum is at the end of its swing. Write a numerical simulation to determine the period of the pendulum for any combination of \(m\), \(L\), and \(\theta\). Examine the effect of changing each variable while manipulating the others.
40. A ball falls from a height \(h\). Without air resistance, the time it takes to reach the floor is \(\sqrt{2h/g}\). A numerical version of this calculation was given in program time2 on page 92. Now suppose that air resistance is not negligible. For a smooth sphere of radius \(r\), moving at speed \(v\) through air of density \(\rho\), the amount of energy \(dQ\) dissipated as heat as the ball falls through a height \(dy\) is given (ignoring signs) by \(dQ = (\pi/4)\rho v^2 r^2 dy\). Modify the program to incorporate this effect, and find the resulting change in the fall time in the case of a 21 g ball of radius 1.0 cm, falling from a height of 1.0 m. The density of air at sea level is about \(1.2\ \text{kg}/\text{m}^3\). Turn in a printout of both your program and its output. Answer: 0.34 ms.
41. The factorial of an integer \(n\), written \(n!\), is defined as the product of all the positive integers less than or equal to \(n\). For example, \(3!=1\times2\times3=6\). Write a Python program to compute the factorial of a number. Test it with a small number whose factorial you can check by hand. Then use it to compute \(30!\). (Python computes integer results with unlimited precision, so you won't get any problems with rounding or overflows.) Turn in a printout of your program and its output, including the test.
42. Estimate the kinetic energy of a buzzing fly's wing.
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


