03. Calculating the Force of Gravity near the Surface of the Earth
( \newcommand{\kernel}{\mathrm{null}\,}\)
Calculating the Force of Gravity near the Surface of the Earth
In addition to creating the three laws of motion mentioned earlier, Newton also postulated the Law of Universal Gravitation. This law states that every object of mass in the universe creates a gravitational field, and every object of mass in the universe senses and interacts with every other objects’ field. That’s an awful lot of forces! To try to identify and estimate the magnitude of all of these forces on an object near the surface of the earth would be a lifelong task.
Luckily, the strength of the gravitational field depends on the mass of the object producing the field. The more massive the object, the stronger the field. Thus, since the earth is much more massive than any other nearby object, when creating free-body diagrams for objects near the surface of the earth we can safely include just the gravitational force due to the earth, ignoring all the other, relatively small, gravitational forces.
The magnitude of the gravitational field of a massive object, denoted g, depends on the mass of the object, the distance from the center of the object, and a constant called, appropriately, the gravitational constant, G. The relationship is:
Near the surface of the earth, the gravitational field has a magnitude of approximately 9.8 N/kg. Although the gravitational field strength varies with the distance from the surface of the earth, we will ignore this slight variation unless explicitly told to include its effects.
The gravitational force felt by a massive object in the presence of a gravitational field is given by the product of the object’s mass and the magnitude of the gravitational field at the location of the object:
Forces are measured in Newtons [N], where,
Applying Newton’s Second Law
Let’s return to the scenario under investigation and make some quantitative information more explicit. Then, we can attempt to further investigate the situation using Newton’s Second Law.
A 30 kg child pulls herself up a rope at an approximately constant speed using only her hands.
Newton’s Second Law states:
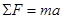
refers to the sum of all of the forces acting on the girl, the force of the rope (which is positive in our coordinate system) and the force of gravity (which is negative in our coordinate system). Thus,
Since m = 30 kg, and a = 0 m/s2 (since she climbs at constant speed), the equation becomes:
By Newton’s relationship for the force of gravity:
Therefore:
Thus, Newton’s Second Law allows us to determine the force with which the rope pulls on the girl. Of course, by Newton’s Third Law, the force with which the girl pulls on the rope is equal in magnitude, so the girl exerts a 294 N force on the rope.
If the girl had not climbed the rope at approximately constant speed her acceleration would have to be determined, either from an explicit mention in the description or through using the kinematic relations developed in the last unit, and then inserted into Newton’s Second Law. If her acceleration had been directed upwards (positive) the force of the rope on the girl would have had to be larger. If her acceleration had been directed downwards (negative) the force of the rope on the girl would have had to be smaller.


