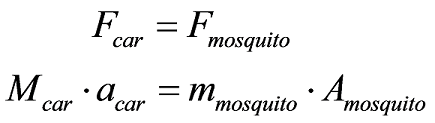05. Hints and Suggestions
- Page ID
- 629
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Magnitude of the Gravitational Field
Quite often, students make a pair of mistakes when dealing with the magnitude of the gravitational field, g.
‘g’ is never negative.
Since g is the magnitude of the gravitational field, it cannot be a negative number. As a magnitude,it does not have a direction associated with it! Resist all temptation to replace ‘g’ with the value “-9.8 N/kg”!
Part of the confusion lies with the fact that the gravitational field does have an associated direction. The gravitational field of the earth is directed downward toward the center of the earth. Even so, the gravitational field is not negative. Negative only makes sense relative to a coordinate system, and since you are always free to choose any system you want, the gravitational field is just as likely to be oriented in the positive as the negative direction.
‘g’ is not an acceleration.
Often times, students have the idea that ‘g’ is the “acceleration due to gravity”. However, as I sit here in a chair writing this book, the force of gravity is acting on me and I am most definitelynot accelerating at 9.8 m/s2! In fact, the force of gravity has acted on me for every second of my life and only very rarely have I accelerated at 9.8 m/s2. ‘g’ measures the strength of the gravitational field. As such, it is related to the gravitational force, which, like all forces, can give raise to accelerations. However, it is the total force acting on an object that determines its acceleration, not simply the force of gravity.
It is true that the units of ‘g’, N/kg, are also the units of acceleration, since a Newton is defined to be a kg m/s2. It is also true that in a very specific scenario, when the only force acting on an object is the force of gravity, the magnitude of the object’s acceleration is numerically equal to ‘g’. However, there are also very specific scenarios in which the acceleration of an object is numerically equal to 4.576 m/s2, or 62.31452 m/s2. The strength of physics is its ability to analyze diverse scenarios with the same small set of tools, not to develop specialized tools tailored to every different specific scenario. Newton’s Second Law will always allow you to determine an object’s acceleration, whether the force of gravity acts alone or not.
Newton’s Third Law
Many physics students have heard the saying, “For every action there is an equal and opposite re-action.” I was forced to memorize this statement in a middle-school science class, and was told it was called Newton’s Third Law. I had no idea what it meant then, and I still am not very clear about what it has to do with Newton’s Third Law.
As a test of your understanding of Newton’s Third Law, try to answer the following question:
As you drive along the highway, a mosquito splats against your car windshield. During the collision between the mosquito and the car:
- the force on the mosquito was greater in magnitude than the force on the car.
- the force on the car was greater in magnitude than the force on the mosquito.
- the force on the mosquito was equal in magnitude to the force on the car.
- it is impossible to determine the relative sizes of the forces without more information.
As strange as it may seem, the correct answer is ‘c’. The forces exerted on the mosquito and the car are equal in magnitude. In the terminology used in this chapter, the mosquito and car interact (probably an unpleasant interaction for the mosquito), and in an interaction the two agents involved exert equal forces on each other.
However, obviously something is different about the interaction from the mosquito’s perspective. What is different is not the force acting on the mosquito but rather its acceleration. Although the forces acting on the mosquito and car are the same, the mosquito’s acceleration is much greater than the car’s acceleration because the mosquito’s mass is much smaller than the car’s mass. The acceleration of the car is so small that it is not even noticed by the driver, while the acceleration of the mosquito is certainly noticed by the mosquito!