03. Applying Newton's Second Law
( \newcommand{\kernel}{\mathrm{null}\,}\)
Applying Newton's Second Law
Using this model for friction, we can now quantitatively analyze the original situation. Note that the two coefficients of friction will typically be given as an ordered pair, (ms, mk).
While rearranging furniture, a 600 N force is applied at an angle of 25°below horizontal to a 100 kg sofa at rest. The coefficient of friction between the sofa and the floor is (0.5, 0.4).
A free-body diagram for the sofa is sketched below:
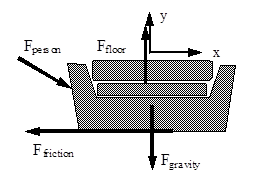
Hopefully you realize that two quite different outcomes can result from this push. Either the person pushes too weakly to move the couch or the push is sufficient to make the couch move. Since the frictional forces acting in these two cases are quite different, we can’t really numerically analyze the situation until we make an assumption as to the outcome of the push. Of course, we will then have to check the validity of our assumption once we have completed our analysis. If our assumption turns out to be incorrect, we will then have to re-analyze the situation using the other possible outcome.
I will assume the couch doesn’t move for the analysis below, and then later check the assumption. Assuming the couch doesn’t move is equivalent to assuming ax = 0 m/s2 and that the relevant type of friction to use is static friction.
Applying Newton’s Second Law independently in the horizontal (x) and vertical (y) directions yields:
x-direction y-direction
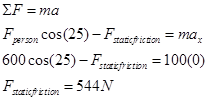
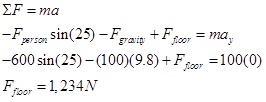
Notice that the acceleration of the couch in the vertical direction must be zero regardless of my assumption, unless the couch begins to levitate or crash through the floor.
Assuming the couch doesn’t move leads to a calculated value of static friction equal to 544 N. Can static friction create a force of this magnitude to prevent the couch’s motion? I can check this calculated value against the allowed values for static friction:
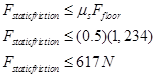
Since the calculated value of the static frictional force is below the maximum possible value of the static frictional force, my analysis and assumption are valid, the couch does not budge. The person is not pushing hard enough to overcome the static frictional force that acts to prevent the couch’s motion relative to the floor.
Therefore, in this scenario the actual value of the static frictional force is 544 N (remember, it can be any value less than or equal to 617 N) and the acceleration of the couch is equal to zero.
How would the analysis change if the couch was initially in motion? Assume you enlisted a friend to help get the couch moving, but as soon as it began to move your friend stopped pushing. Would the couch stop immediately, gradually slow down to a stop, or could you keep the couch in motion across the room?
If the couch was initially moving, two things must change in our analysis. First, the horizontal acceleration of the couch is no longer necessarily zero. Second, the frictional force acting on the couch is kinetic.
Applying Newton’s Second Law independently in the horizontal (x) and vertical (y) directions now yields:
x-direction y-direction
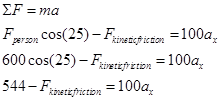
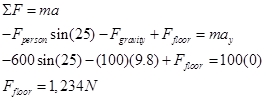
To finish the analysis, we need to calculate the kinetic frictional force.
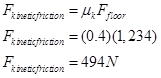
Substituting this into the x-equation above yields:
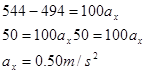
Thus, if the couch is already moving the kinetic frictional force is 494 N and the couch accelerates toward the right at 0.50 m/s2. In summary, if the couch is initially moving it will continue to move and accelerate at 0.50 m/s2 to the right. If it is initially at rest, the person pushing on it will not be able to get it to move.


