04. Choosing a Coordinate System
( \newcommand{\kernel}{\mathrm{null}\,}\)
Choosing a Coordinate System
In analyzing a scenario, you are always free to choose whatever coordinate system you like. If you make up negative, or left positive, this will not make you get the wrong answer. However, certain coordinate systems may make the mathematical analysis simpler than other coordinate systems. For example;
A 75 kg skier starts from rest at the top of a 200 slope. He’s a show-off, so he skies down the hill backward. The frictional coefficient between his skies and the snow is (0.10,0.05).
In attempting to analyze this situation, first draw a free-body diagram.
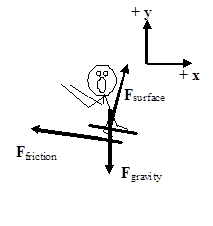
Notice that I have chosen the traditional horizontal and vertical coordinate system. I could analyze the situation using this coordinate system, but there are two difficulties with this choice.
- Neither the force of the surface nor the force of friction is oriented in the x- or y-direction. (The force of gravity is oriented in the negative y-direction.) Therefore, I will have to use trigonometry to determine the x- and y-components of both of these forces.
- The skier is accelerating down the inclined slope. Thus, I will also need trigonometry to determine the x- and y-components of the acceleration.
Although these difficulties are by no means insurmountable, why make the task more difficult than it has to be?
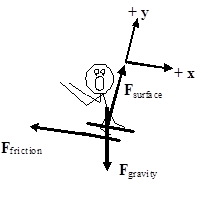
Contrast the above choice of coordinate system with a coordinate system in which the x-direction is tilted parallel to the surface on which the skier slides and the y-direction, remaining perpendicular to the x, is perpendicular to the surface.
- Using the tilted coordinate system, the only force not oriented in the x- or y-direction is the force of gravity. Therefore, I will only need to use trigonometry to determine the x- and y-components of one force rather than two.
- The skier is accelerating down the inclined slope. Since the x-direction is oriented parallel to the slope, the skier has an acceleration in the x-direction and zero acceleration in the y-direction.
This simple rotation of the coordinate system has made the mathematical analysis of this situation much easier. Applying Newton’s second law in the x- and y-direction leads to:

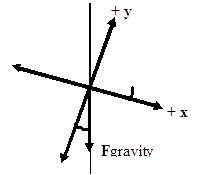
Notice that if the x-axis is rotated by 200 from horizontal to become parallel to the slope, the y-axis is rotated by 200 from vertical. Since the force of gravity is always oriented vertically downward, it's now 200from the y-axis.
Thus, the force of gravity has a component in the positive x-direction of Fgravity (sin 200) and a component in the negative y-direction of Fgravity (cos 200).
Now that the contact force between the skier and the slope is known, the static friction force can be determined.

Since the x-component of the force of gravity on the skier (251 N) is larger than the force of static friction (69 N), the skier will accelerate down the hill. Once he begins to move, the frictional force must be calculated using the kinetic friction model.

Examining the x-component of Newton’s second law:
251 - Ffriction= 75 ax
251 - 35 = 75 ax
ax= 2.9 m/s2
The skier accelerates down the slope with an acceleration of 2.9 m/s2.


