7.8: Work, Energy, and Power in Humans

Learning Objectives

By the end of this section, you will be able to:

• Explain the human body’s consumption of energy when at rest vs. when engaged in activities that do useful work.
• Calculate the conversion of chemical energy in food into useful work.

Energy Conversion in Humans

Our own bodies, like all living organisms, are energy conversion machines. Conservation of energy implies that the chemical energy stored in food is converted into work, thermal energy, and/or stored as chemical energy in fatty tissue. (Figure 7.09.1.) The fraction going into each form depends both on how much we eat and on our level of physical activity. If we eat more than is needed to do work and stay warm, the remainder goes into body fat.

Figure \(\PageIndex{1}\): Energy consumed by humans is converted to work, thermal energy, and stored fat. By far the largest fraction goes to thermal energy, although the fraction varies depending on the type of physical activity.

Power Consumed at Rest

The rate at which the body uses food energy to sustain life and to do different activities is called the metabolic rate. The total energy conversion rate of a person at rest is called the basal metabolic rate (BMR) and is divided among various systems in the body, as shown in Table. The largest fraction goes to the liver and spleen, with the brain coming next. Of course, during vigorous exercise, the energy consumption of the skeletal muscles and heart increase markedly. About 75% of the calories burned in a day go into these basic functions. The BMR is a function of age, gender, total body weight, and amount of muscle mass (which burns more calories than body fat). Athletes have a greater BMR due to this last factor.

Basal Metabolic Rates (BMR):

Organ	Power consumed at rest (W)	Oxygen consumption (mL/min)	Percent of BMR
Liver & spleen	23	67	27
Brain	16	47	19
Skeletal muscle	15	45	18
Kidney	9	26	10
Heart	6	17	7
Other	16	48	19
Totals	85 W	250 mL/min	100%

Energy consumption is directly proportional to oxygen consumption because the digestive process is basically one of oxidizing food. We can measure the energy people use during various activities by measuring their oxygen use. (See Figure7.09.1.) Approximately 20 kJ of energy are produced for each liter of oxygen consumed, independent of the type of food. Table shows energy and oxygen consumption rates (power expended) for a variety of activities.

Power of Doing Useful Work

Work done by a person is sometimes called useful work, which is work done on the outside world, such as lifting weights. Useful work requires a force exerted through a distance on the outside world, and so it excludes internal work, such as that done by the heart when pumping blood. Useful work does include that done in climbing stairs or accelerating to a full run, because these are accomplished by exerting forces on the outside world. Forces exerted by the body are non-conservative, so that they can change the mechanical energy \((KE + PE)\) of the system worked upon, and this is often the goal. A baseball player throwing a ball, for example, increases both the ball’s kinetic and potential energy.

If a person needs more energy than they consume, such as when doing vigorous work, the body must draw upon the chemical energy stored in fat. So exercise can be helpful in losing fat. However, the amount of exercise needed to produce a loss in fat, or to burn off extra calories consumed that day, can be large, as Example 7.09.1 illustrates.

Example \(\PageIndex{1}\): Calculating Weight Loss from Exercising

If a person who normally requires an average of 12,000 kJ (3000 kcal) of food energy per day consumes 13,000 kJ per day, he will steadily gain weight. How much bicycling per day is required to work off this extra 1000 kJ?

Solution

Table states that 400 W are used when cycling at a moderate speed. The time required to work off 1000 kJ at this rate is then

\[Time = \dfrac{energy}{\left(\frac{energy}{time} \right)} = \dfrac{1000 \, kJ}{400 \, W} = 2500 \, s = 42 \, min.\]

Discussion

If this person uses more energy than he or she consumes, the person’s body will obtain the needed energy by metabolizing body fat. If the person uses 13,000 kJ but consumes only 12,000 kJ, then the amount of fat loss will be

\[ Fat \, loss = (1000 \, kJ) \left ( \frac{1 \, g \, fat}{30 \, kJ} \right) = 26 \, g,\]

assuming the energy content of fat to be 39 kJ/g.

Figure \(\PageIndex{2}\): A pulse oxymeter is an apparatus that measures the amount of oxygen in blood. A knowledge of oxygen and carbon dioxide levels indicates a person’s metabolic rate, which is the rate at which food energy is converted to another form. a person’s metabolic rate, which is the rate at which food energy is converted to another form. Such measurements can indicate the level of athletic conditioning as well as certain medical problems. (credit: UusiAjaja, Wikimedia Commons)

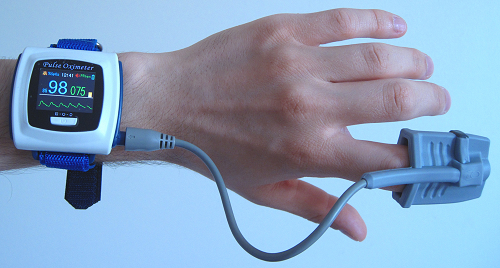
Energy and Oxygen Consumption Rates:

Activity	Energy consumption in watts	Oxygen consumption in liters O2/min
Sleeping	83	0.24
Sitting at rest	120	0.34
Standing relaxed	125	0.36
Sitting in class	210	0.60
Walking (5 km/h)	280	0.80
Cycling (13–18 km/h)	400	1.14
Shivering	425	1.21
Playing tennis	440	1.26
Swimming breaststroke	475	1.36
Ice skating (14.5 km/h)	545	1.56
Climbing stairs (116/min)	685	1.96
Cycling (21 km/h)	700	2.00
Running cross-country	740	2.12
Playing basketball	800	2.28
Cycling, professional racer	1855	5.30
Sprinting	2415	6.90

All bodily functions, from thinking to lifting weights, require energy. (See Figure 7.09.3.) The many small muscle actions accompanying all quiet activity, from sleeping to head scratching, ultimately become thermal energy, as do less visible muscle actions by the heart, lungs, and digestive tract. Shivering, in fact, is an involuntary response to low body temperature that pits muscles against one another to produce thermal energy in the body (and do no work). The kidneys and liver consume a surprising amount of energy, but the biggest surprise of all it that a full 25% of all energy consumed by the body is used to maintain electrical potentials in all living cells. (Nerve cells use this electrical potential in nerve impulses.) This bioelectrical energy ultimately becomes mostly thermal energy, but some is utilized to power chemical processes such as in the kidneys and liver, and in fat production.

Figure \(\PageIndex{3}\): This MRI scan shows an increased level of energy consumption in the vision center of the brain. Here, the patient was being asked to recognize faces. (credit: NIH via Wikimedia Commons)

Summary

• The human body converts energy stored in food into work, thermal energy, and/or chemical energy that is stored in fatty tissue.
• The rate at which the body uses food energy to sustain life and to do different activities is called the metabolic rate, and the corresponding rate when at rest is called the basal metabolic rate (BMR)
• The energy included in the basal metabolic rate is divided among various systems in the body, with the largest fraction going to the liver and spleen, and the brain coming next.
• About 75% of food calories are used to sustain basic body functions included in the basal metabolic rate.
• The energy consumption of people during various activities can be determined by measuring their oxygen use, because the digestive process is basically one of oxidizing food.

Glossary

metabolic rate

the rate at which the body uses food energy to sustain life and to do different activities

basal metabolic rate

the total energy conversion rate of a person at rest

useful work

work done on an external system