Problems & Exercises
24. Find the ratio of speeds of an electron and a negative hydrogen ion (one having an extra electron) accelerated through the same voltage, assuming non-relativistic final speeds. Take the mass of the hydrogen ion to be \(1.67\times 10^{-27}\: \mathrm{kg}\).
Solution
\(42.8\)
25. An evacuated tube uses an accelerating voltage of 40 kV to accelerate electrons to hit a copper plate and produce x rays. Non-relativistically, what would be the maximum speed of these electrons?
26. A bare helium nucleus has two positive charges and a mass of \(6.64\times 10^{-27}\: \mathrm{kg}\)
(a) Calculate its kinetic energy in joules at 2.00% of the speed of light.
(b) What is this in electron volts?
(c) What voltage would be needed to obtain this energy?
27. Integrated Concepts
Singly charged gas ions are accelerated from rest through a voltage of 13.0 V. At what temperature will the average kinetic energy of gas molecules be the same as that given these ions?
Solution
\(1.00\times 10^{5}\: \mathrm{K}\)
28. Integrated Concepts
The temperature near the center of the Sun is thought to be 15 million degrees Celsius (\(1.5\times{10^{7}}^{\circ}C\)).Through what voltage must a singly charged ion be accelerated to have the same energy as the average kinetic energy of ions at this temperature?
29. Integrated Concepts
(a) What is the average power output of a heart defibrillator that dissipates 400 J of energy in 10.0 ms?
(b) Considering the high-power output, why doesn’t the defibrillator produce serious burns?
Solution
(a)\(4\times 10^{4}\: \mathrm{W}\)
(b) A defibrillator does not cause serious burns because the skin conducts electricity well at high voltages, like those used in defibrillators. The gel used aids in the transfer of energy to the body, and the skin doesn’t absorb the energy, but rather lets it pass through to the heart.
30. Integrated Concepts
A lightning bolt strikes a tree, moving 20.0 C of charge through a potential difference of \(1.00\times 10^{2}\: \mathrm{MV}\). (a) What energy was dissipated? (b) What mass of water could be raised from \(15^{\circ}C\) to the boiling point and then boiled by this energy? (c) Discuss the damage that could be caused to the tree by the expansion of the boiling steam.
31. Integrated Concepts
A 12.0 V battery-operated bottle warmer heats 50.0 g of glass, \(2.50\times 10^{2}\: \mathrm{g}\) of baby formula, and \(2.00\times 10^{2}\: \mathrm{g}\) of aluminum from \(20.0^{\circ}C\) to \(90.0^{\circ}C\).
(a) How much charge is moved by the battery?
(b) How many electrons per second flow if it takes 5.00 min to warm the formula? (Hint: Assume that the specific heat of baby formula is about the same as the specific heat of water.)
Solution
(a)\(7.40\times 10^{3}\: \mathrm{C}\)
(b)\(1.54\times 10^{20}\: \mathrm{electrons\: per\: second}\)
32. Integrated Concepts
A battery-operated car utilizes a 12.0 V system. Find the charge the batteries must be able to move in order to accelerate the 750 kg car from rest to 25.0 m/s, make it climb a \(2.00\times 10^{2}\: \mathrm{m}\) high hill, and then cause it to travel at a constant 25.0 m/s by exerting a \(5.00\times 10^{2}\: \mathrm{N}\) force for an hour.
Solution
\(3.89\times 10^{6}\: \mathrm{C}\)
33. Integrated Concepts
Fusion probability is greatly enhanced when appropriate nuclei are brought close together, but mutual Coulomb repulsion must be overcome. This can be done using the kinetic energy of high-temperature gas ions or by accelerating the nuclei toward one another. (a) Calculate the potential energy of two singly charged nuclei separated by \(1.00\times 10^{-12}\: \mathrm{m}\) by finding the voltage of one at that distance and multiplying by the charge of the other. (b) At what temperature will atoms of a gas have an average kinetic energy equal to this needed electrical potential energy?
34. Unreasonable Results
(a) Find the voltage near a 10.0 cm diameter metal sphere that has 8.00 C of excess positive charge on it.
(b) What is unreasonable about this result?
(c) Which assumptions are responsible?
Solution
(a)\(1.44\times 10^{12}\: \mathrm{V}\)
(b) This voltage is very high. A 10.0 cm diameter sphere could never maintain this voltage; it would discharge.
(c) An 8.00 C charge is more charge than can reasonably be accumulated on a sphere of that size.
35. Construct Your Own Problem
Consider a battery used to supply energy to a cellular phone. Construct a problem in which you determine the energy that must be supplied by the battery, and then calculate the amount of charge it must be able to move in order to supply this energy. Among the things to be considered are the energy needs and battery voltage. You may need to look ahead to interpret manufacturer’s battery ratings in ampere-hours as energy in joules.
36. Show that units of V/m and N/C for electric field strength are indeed equivalent.
37. What is the strength of the electric field between two parallel conducting plates separated by 1.00 cm and having a potential difference (voltage) between them of \(1.50\times 10^{4}\: \mathrm{V}\)?
38. The electric field strength between two parallel conducting plates separated by 4.00 cm is \(7.50\times 10^{4}\: \mathrm{V/m}\).
(a) What is the potential difference between the plates?
(b) The plate with the lowest potential is taken to be at zero volts. What is the potential 1.00 cm from that plate (and 3.00 cm from the other)?
Solution
(a)\(3.00\: \mathrm{kV}\)
(b)\(750\: \mathrm{V}\)
39. How far apart are two conducting plates that have an electric field strength of \(4.50\times 10^{3}\: \mathrm{V/m}\) between them, if their potential difference is 15.0 kV?
40. (a) Will the electric field strength between two parallel conducting plates exceed the breakdown strength for air (\(3.0\times 10^{6}\: \mathrm{V/m}\)) if the plates are separated by 2.00 mm and a potential difference of \(5.0\times 10^{3}\: \mathrm{V}\) is applied?
(b) How close together can the plates be with this applied voltage?
Solution
(a) No. The electric field strength between the plates is \(2.5\times 10^{6}\: \mathrm{V/m}\) which is lower than the breakdown strength for air (\(3.0\times 10^{6}\: \mathrm{V/m}\)).
(b)\(1.7\: \mathrm{mm}\)
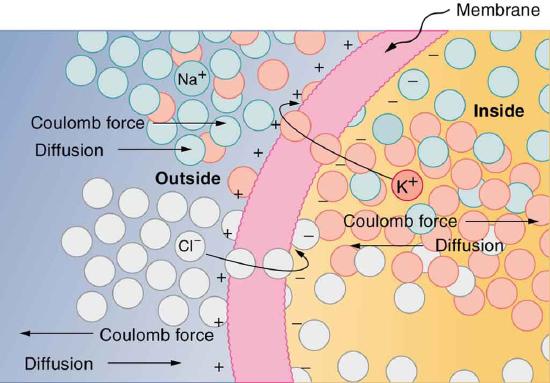
41. The voltage across a membrane forming a cell wall is 80.0 mV and the membrane is 9.00 nm thick. What is the electric field strength? (The value is surprisingly large, but correct. Membranes are discussed inCapacitors and Dielectrics and Nerve Conduction—Electrocardiograms.) You may assume a uniform electric field.
42. Membrane walls of living cells have surprisingly large electric fields across them due to separation of ions. (Membranes are discussed in some detail in Nerve Conduction—Electrocardiograms.) What is the voltage across an 8.00 nm–thick membrane if the electric field strength across it is 5.50 MV/m? You may assume a uniform electric field.
Solution
\(44.0\: \mathrm{mV}\)
43. Two parallel conducting plates are separated by 10.0 cm, and one of them is taken to be at zero volts.
(a) What is the electric field strength between them, if the potential 8.00 cm from the zero volt plate (and 2.00 cm from the other) is 450 V?
(b) What is the voltage between the plates?
44. Find the maximum potential difference between two parallel conducting plates separated by 0.500 cm of air, given the maximum sustainable electric field strength in air to be \(3.0\times 10^{6}\: \mathrm{V/m}\).
Solution
\(15\: \mathrm{kV}\)
45. A doubly charged ion is accelerated to an energy of 32.0 keV by the electric field between two parallel conducting plates separated by 2.00 cm. What is the electric field strength between the plates?
46. An electron is to be accelerated in a uniform electric field having a strength of \(2.00\times 10^{6}\: \mathrm{V/m}\).
(a) What energy in keV is given to the electron if it is accelerated through 0.400 m?
(b) Over what distance would it have to be accelerated to increase its energy by 50.0 GeV?
Solution
(a)\(800\: \mathrm{KeV}\)
(b)\(25.0\: \mathrm{km}\)
47. A 0.500 cm diameter plastic sphere, used in a static electricity demonstration, has a uniformly distributed 40.0 pC charge on its surface. What is the potential near its surface?
Solution
\(144\: \mathrm{V}\)
48. What is the potential \(0.530\times 10^{-10}\: \mathrm{m}\) from a proton (the average distance between the proton and electron in a hydrogen atom)?
49. (a) A sphere has a surface uniformly charged with 1.00 C. At what distance from its center is the potential 5.00 MV?
(b) What does your answer imply about the practical aspect of isolating such a large charge?
Solution
(a) 1.80 km
(b) A charge of 1 C is a very large amount of charge; a sphere of radius 1.80 km is not practical.
50. How far from a \(1.00\: \mu \mathrm{C}\) point charge will the potential be 100 V? At what distance will it be \(2.00\times 10^{2}\: \mathrm{V}\)?
51. What are the sign and magnitude of a point charge that produces a potential of \(-2.00\: \mathrm{V}\) at a distance of 1.00 mm?
Solution
\(-2.22\times 10^{-13}\: \mathrm{C}\)
52. If the potential due to a point charge is \(5.00\times 10^{2}\: \mathrm{V}\) at a distance of 15.0 m, what are the sign and magnitude of the charge?
53. In nuclear fission, a nucleus splits roughly in half.
(a) What is the potential \(2.00\times 10^{-14}\: \mathrm{m}\) from a fragment that has 46 protons in it?
(b) What is the potential energy in MeV of a similarly charged fragment at this distance?
Solution
(a)\(3.31\times 10^{6}\: \mathrm{V}\)
(b)\(152\: \mathrm{MeV}\)
54. A research Van de Graaff generator has a 2.00-m-diameter metal sphere with a charge of 5.00 mC on it.
(a) What is the potential near its surface?
(b) At what distance from its center is the potential 1.00 MV?
(c) An oxygen atom with three missing electrons is released near the Van de Graaff generator. What is its energy in MeV at this distance?
55. An electrostatic paint sprayer has a 0.200-m-diameter metal sphere at a potential of 25.0 kV that repels paint droplets onto a grounded object.
(a) What charge is on the sphere?
(b) What charge must a 0.100-mg drop of paint have to arrive at the object with a speed of 10.0 m/s?
Solution
(a)\(2.78\times10^{-7}\: \mathrm{C}\)
(b)\(2.00\times 10^{-10}\: \mathrm{C}\)
56. In one of the classic nuclear physics experiments at the beginning of the 20th century, an alpha particle was accelerated toward a gold nucleus, and its path was substantially deflected by the Coulomb interaction. If the energy of the doubly charged alpha nucleus was 5.00 MeV, how close to the gold nucleus (79 protons) could it come before being deflected?
57. (a) What is the potential between two points situated 10 cm and 20 cm from a \(3.0\: \mu \mathrm{C}\) point charge?
(b) To what location should the point at 20 cm be moved to increase this potential difference by a factor of two?
58. Unreasonable Results
(a) What is the final speed of an electron accelerated from rest through a voltage of 25.0 MV by a negatively charged Van de Graaff terminal?
(b) What is unreasonable about this result?
(c) Which assumptions are responsible?
Solution
(a)\(2.96\times 10^{9}\: \mathrm{m/s}\)
(b) This velocity is far too great. It is faster than the speed of light.
(c) The assumption that the speed of the electron is far less than that of light and that the problem does not require a relativistic treatment produces an answer greater than the speed of light.
59. (a) Sketch the equipotential lines near a point charge +\(q\). Indicate the direction of increasing potential.
(b) Do the same for a point charge \(-3q\).
60. Sketch the equipotential lines for the two equal positive charges shown in Figure 19.5.6. Indicate the direction of increasing potential.
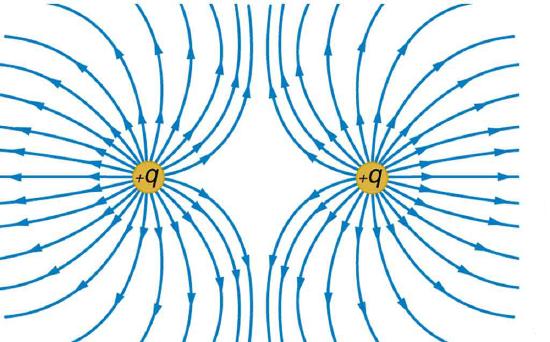
Figure 19.5.6: The electric field near two equal positive charges is directed away from each of the charges.
61. Figure 19.5.7 shows the electric field lines near two charges \(q_{1}\) and \(q_{2}\), the first having a magnitude four times that of the second. Sketch the equipotential lines for these two charges, and indicate the direction of increasing potential.
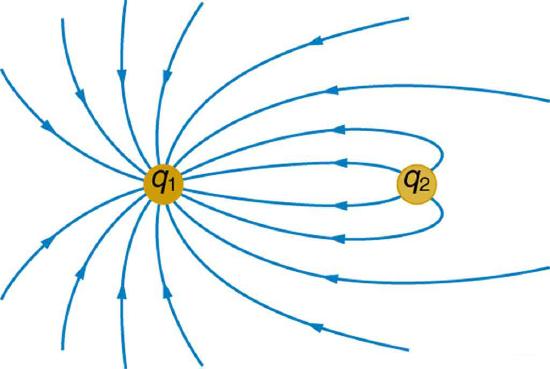
The electric field near two charges.
62. Sketch the equipotential lines a long distance from the charges shown in Figure 19.5.7. Indicate the direction of increasing potential.
63. Sketch the equipotential lines in the vicinity of two opposite charges, where the negative charge is three times as great in magnitude as the positive. See Figure 19.5.7 for a similar situation. Indicate the direction of increasing potential.
64. Sketch the equipotential lines in the vicinity of the negatively charged conductor in Figure 19.5.8. How will these equipotentials look a long distance from the object?

Figure 19.5.8: A negatively charged conductor.
65. Sketch the equipotential lines surrounding the two conducting plates shown in Figure 19.5.9, given the top plate is positive and the bottom plate has an equal amount of negative charge. Be certain to indicate the distribution of charge on the plates. Is the field strongest where the plates are closest? Why should it be?
Figure 19.5.9
66. (a) Sketch the electric field lines in the vicinity of the charged insulator in Figure 19.5.10. Note its non-uniform charge distribution. (b) Sketch equipotential lines surrounding the insulator. Indicate the direction of increasing potential.
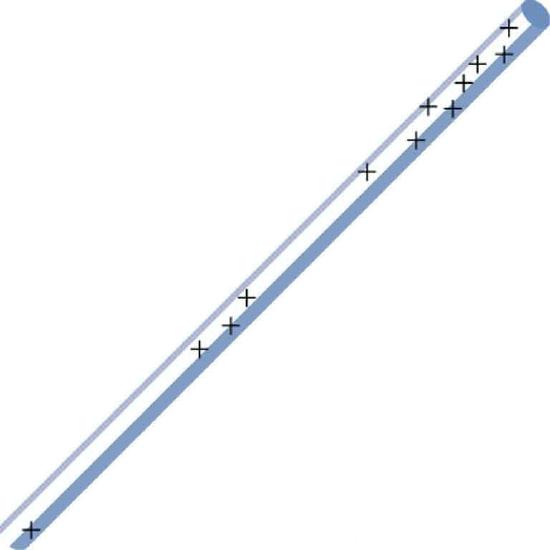
Figure 19.5.10: A charged insulating rod such as might be used in a classroom demonstration.
67. The naturally occurring charge on the ground on a fine day out in the open country is \(-1.00\: \mathrm{nC/m^{2}}\).
(a) What is the electric field relative to ground at a height of 3.00 m?
(b) Calculate the electric potential at this height.
(c) Sketch electric field and equipotential lines for this scenario.
68. The lesser electric ray (Narcine bancroftii) maintains an incredible charge on its head and a charge equal in magnitude but opposite in sign on its tail (Figure).
(a) Sketch the equipotential lines surrounding the ray.
(b) Sketch the equipotentials when the ray is near a ship with a conducting surface.
(c) How could this charge distribution be of use to the ray?

Figure 19.5.11: Lesser electric ray (Narcine bancroftii) (credit: National Oceanic and Atmospheric Administration, NOAA's Fisheries Collection).
69. What charge is stored in a \(180\: \mu \mathrm{F}\) capacitor when 120 V is applied to it?
Solution
\(21.6\: \mathrm{mC}\)
70. Find the charge stored when 5.50 V is applied to an 8.00 pF capacitor.
71. What charge is stored in the capacitor in Example?
Solution
\(80.0\: \mathrm{mC}\)
72. Calculate the voltage applied to a \(2.00\: \mu \mathrm{F}\) capacitor when it holds \(3.10\: \mu \mathrm{C}\) of charge.
73. What voltage must be applied to an 8.00 nF capacitor to store 0.160 mC of charge?
Solution
20.0 kV
74. What capacitance is needed to store \(3.00\: \mu \mathrm{C}\) of charge at a voltage of 120 V?
75. What is the capacitance of a large Van de Graaff generator’s terminal, given that it stores 8.00 mC of charge at a voltage of 12.0 MV?
Solution
\(667\: \mathrm{pF}\)
76. Find the capacitance of a parallel plate capacitor having plates of area \(5.00\: \mathrm{m^{2}}\) that are separated by 0.100 mm of Teflon.
77. (a)What is the capacitance of a parallel plate capacitor having plates of area \(1.50\: \mathrm{m^{2}}\) that are separated by 0.0200 mm of neoprene rubber?
(b) What charge does it hold when 9.00 V is applied to it?
Solution
(a)\(4.4\: \mu \mathrm{F}\)
(b)\(4.0\times 10^{-5}\: \mathrm{C}\)
78. Integrated Concepts
A prankster applies 450 V to an \(80.0\: \mu \mathrm{F}\) capacitor and then tosses it to an unsuspecting victim. The victim’s finger is burned by the discharge of the capacitor through 0.200 g of flesh. What is the temperature increase of the flesh? Is it reasonable to assume no phase change?
79. Unreasonable Results
(a) A certain parallel plate capacitor has plates of area \(4.00\: \mathrm{m^{2}}\), separated by 0.0100 mm of nylon, and stores 0.170 C of charge. What is the applied voltage?
(b) What is unreasonable about this result?
(c) Which assumptions are responsible or inconsistent?
Solution
(a) 14.2 kV
(b) The voltage is unreasonably large, more than 100 times the breakdown voltage of nylon.
(c) The assumed charge is unreasonably large and cannot be stored in a capacitor of these dimensions.
80. Find the total capacitance of the combination of capacitors in Figure 19.7.4.
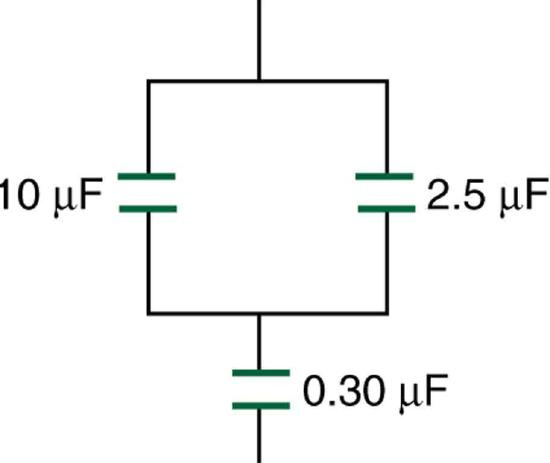
Figure 19.7.4: A combination of series and parallel connections of capacitors.
Solution
\(0.293\: \mu \mathrm{F}\)
81. Suppose you want a capacitor bank with a total capacitance of 0.750 F and you possess numerous 1.50 mF capacitors. What is the smallest number you could hook together to achieve your goal, and how would you connect them?
82. What total capacitances can you make by connecting a \(5.00\: \mu \mathrm{F}\) and an \(8.00\: \mu \mathrm{F}\) capacitor together?
Solution
\(3.08\: \mu \mathrm{F}\) in series combination, \(13.0\: \mu \mathrm{F}\) in parallel combination
83. Find the total capacitance of the combination of capacitors shown in Figure 19.7.5.
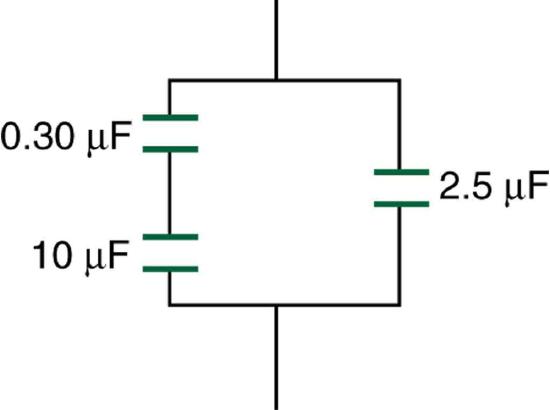
Figure 19.7.5: A combination of series and parallel connections of capacitors.
Solution
\(2.79\: \mu \mathrm{F}\)
84. Find the total capacitance of the combination of capacitors shown in Figure.
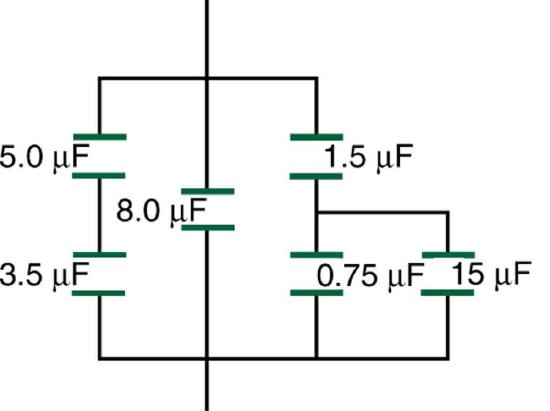
Figure 19.7.6: A combination of series and parallel connections of capacitors.
85. (a) An \(8.00\: \mu \mathrm{F}\) capacitor is connected in parallel to another capacitor, producing a total capacitance of \(5.00\: \mu \mathrm{F}\). What is the capacitance of the second capacitor?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
Solution
(a)\(-3.00\: \mu \mathrm{F}\)
(b) You cannot have a negative value of capacitance.
(c) The assumption that the capacitors were hooked up in parallel, rather than in series, was incorrect. A parallel connection always produces a greater capacitance, while here a smaller capacitance was assumed. This could happen only if the capacitors are connected in series.
86. (a) What is the energy stored in the \(10.0\: \mu \mathrm{F}\) capacitor of a heart defibrillator charged to \(9.00\times 10^{3}\: \mathrm{V}\)?
(b) Find the amount of stored charge.
Solution
(a)\(405\: \mathrm{J}\)
(b)\(90.0\: \mathrm{mC}\)
87. In open heart surgery, a much smaller amount of energy will defibrillate the heart.
(a) What voltage is applied to the \(8.00\: \mu \mathrm{F}\) capacitor of a heart defibrillator that stores 40.0 J of energy?
(b) Find the amount of stored charge.
Solution
(a) 3.16 kV
(b) 25.3 mC
88. A \(165\: \mu \mathrm{F}\) capacitor is used in conjunction with a motor. How much energy is stored in it when 119 V is applied?
89. Suppose you have a 9.00 V battery, a \(2.00\: \mu \mathrm{F}\) capacitor, and a \(7.40\: \mu \mathrm{F}\) capacitor.
(a) Find the charge and energy stored if the capacitors are connected to the battery in series.
(b) Do the same for a parallel connection.
Solution
(a)\(1.42\times 10^{-5}\: \mathrm{C},\: 6.38\times 10^{-5}\: \mathrm{J}\)
(b)\(8.46\times 10^{-5}\: \mathrm{C},\: 3.81\times 10^{-4}\: \mathrm{J}\)
90. A nervous physicist worries that the two metal shelves of his wood frame bookcase might obtain a high voltage if charged by static electricity, perhaps produced by friction.
(a) What is the capacitance of the empty shelves if they have area \(1.00\times 10^{2}\: \mathrm{m^{2}}\) and are 0.200 m apart?
(b) What is the voltage between them if opposite charges of magnitude 2.00 nC are placed on them?
(c) To show that this voltage poses a small hazard, calculate the energy stored.
Solution
(a)\(4.43\times 10^{-12}\: \mathrm{F}\)
(b)\(452\: \mathrm{V}\)
(c)\(4.52\times 10^{-7}\: \mathrm{J}\)
91. Show that for a given dielectric material the maximum energy a parallel plate capacitor can store is directly proportional to the volume of dielectric (\(\mathrm{Volume}\: =A\cdot d\)). Note that the applied voltage is limited by the dielectric strength.
92. Construct Your Own Problem
Consider a heart defibrillator similar to that discussed in Example. Construct a problem in which you examine the charge stored in the capacitor of a defibrillator as a function of stored energy. Among the things to be considered are the applied voltage and whether it should vary with energy to be delivered, the range of energies involved, and the capacitance of the defibrillator. You may also wish to consider the much smaller energy needed for defibrillation during open-heart surgery as a variation on this problem.
93. (a) On a particular day, it takes \(9.60\times 10^{3}\: \mathrm{J}\) of electric energy to start a truck’s engine. Calculate the capacitance of a capacitor that could store that amount of energy at 12.0 V.
(b) What is unreasonable about this result?
(c) Which assumptions are responsible?
Solution
(a)\(133\: \mathrm{F}\)
(b) Such a capacitor would be too large to carry with a truck. The size of the capacitor would be enormous.
(c) It is unreasonable to assume that a capacitor can store the amount of energy needed.