03. Analysis Tools 2
( \newcommand{\kernel}{\mathrm{null}\,}\)
Applying Work-Energy with Gravitational Potential Energy
Let’s use the work-energy relation, with gravitational potential energy terms, to analyze the following scenario:
A 30 kg child on his 15 kg sled slides down his parents’ 10 m long, 150above horizontal driveway after an ice storm. The coefficient of friction between the sled and the driveway is (0.10, 0.08).
Event 1: The instant before the sled begins to move.
Event 2: The instant the sled reaches the bottom of the driveway.
To calculate the gravitational energy terms, let the bottom of the driveway be zero and up positive. The coordinate system used to calculate gravitational energy does not in general have to be the same as the system you use for the rest of the problem. In fact, since the work-energy relation is a scalar equation, the other portions of the equation should not depend on your choice of coordinate system at all!
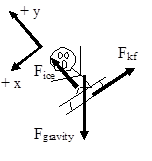
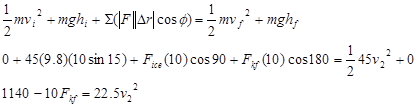
Note:
- The only forces that could do work are the force of the ice and the force of friction, since the action of the force of gravity is already incorporated into the gravitational potential energy terms.
- The heights in the gravitational potential energy function were measured from the bottom of the driveway, with the positive direction as upward, as required. Notice that the initial height is not the same as the length of the driveway. Since the driveway is 10 m long, at an angle of 15°, the height of the top of the driveway relative to the bottom is (10 m) sin 15°. The height at the bottom of the driveway is defined to be 0 m.
To finish the analysis we need to determine the kinetic frictional force. Since this depends on the force of the ice, apply Newton’s Second Law in the y-direction and find:
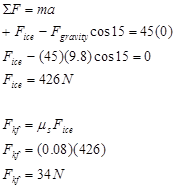
Plugging this value into the work-energy relation yields:
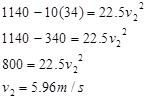
A Two-Dimensional Collision
Let’s try a two-dimensional collision.
At a busy intersection, an impatient driver heading south runs a red-light and collides with a delivery truck originally moving at 15 m/s west. The vehicles become entangled and the skid marks from the wreckage are at 22o south of west. The auto mass is 755 kg and the truck mass is 1250 kg.
I’ll choose:
Event 1: The instant before the car and truck collide.
Event 2: The instant the car and truck reach a common velocity
Partial free-body diagrams (top view) for both the car and the truck during this time interval are shown below.
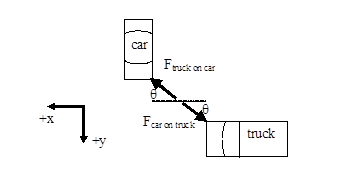
These are only partial free-body diagrams because:
- Forces perpendicular to the earth’s surface (the force of gravity and the force of the road) are not shown.
- During a collision, the force between the colliding objects is normally much greater in magnitude than any other forces acting on the objects. Therefore we will often ignore the other forces acting on colliding objects for the duration of a collision. This approximation is termed the impulse approximation. Under the impulse approximation, the frictional forces between the car and truck and the road are ignored.
Also note that the direction of the force acting between the car and truck is unknown. The angle qis not determined from the situation description.
Applying the impulse-momentum relation to the car and truck yields:
Car
x-direction y-direction
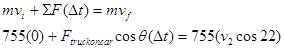
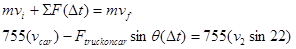
Truck
x-direction y-direction
![]()
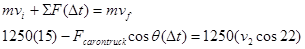
Since the magnitude of the force on the car due to the truck andd the force on the truck due to the car are equal, when the x-equations for the car and truck are added, the impulses cancel!
x-direction
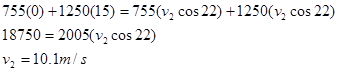
This is the speed of the wreckage immediately after the collision. Note that this is exactly the same equation we would have written if we had considered the system of the car and truck right from the start.
Adding the two y-equations yields:
y-direction
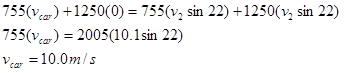
This is the speed of the car immediately before colliding with the truck.


