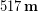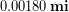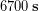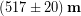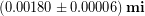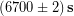3.4: Working with Uncertainties*
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Certainty of Uncertainty
No measurement can be completely error free, infinitely precise, or perfectly accurate. Therefore we can never be absolutely certain of the actual value of a physical quantity we are attempting to measure. We can be certain that all measurement results have uncertainty associated with them. Scientists try to reduce uncertainty as much as is practical and then use a variety of methods, some simple and some very sophisticated, to determine the size of the uncertainty in measured results so that it can be reported along with the results. In this textbook we will stick to the simple methods, if you decide to continue studying science you will learn some of the more sophisticated methods[1][2].
Uncertainty in Tyler’s Pupillary Distance Measurement
There are various statistical methods[3] to determine the uncertainty in Tyler’s set of measurements, but we will just look at the range of values to get a quick idea of the uncertainty in his measurement. We look at the seven values and the average and we notice that the values go up to 2 mm above the average and down to 2 mm below the average.
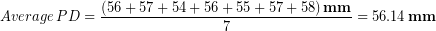
We will use 2 mm as a rough estimate of the uncertainty, which is probably an over-estimate, but it puts us on the safe-side so we don’t underestimate the uncertainty. If we wanted to show the final result of Tyler’s measurements including uncertainty in the standard way then we would write:

Notice that we have rounded the result to drop the decimal places from his result. This is because it would be meaningless to include decimals in the hundredth of a mm place if we don’t even know the answer to within 2 mm, which is in the one mm place. Dropping the decimal places changes the number of significant figures in our result match our uncertainty. The significant figures in a result are those digits that contribute to showing how accurately we know the result.
Significant Figures
Special consideration is given to zeros when counting significant figures. The zeros in 0.053 are not significant, because they are only placeholders that locate the decimal point. There are two significant figures in 0.053. The zeros in 10.053 are not placeholders but are significant—this number has five significant figures. The zeros in 1300 may or may not be significant depending on the style of writing numbers. They could mean the number is known to the last digit, or they could be placeholders. So 1300 could have two, three, or four significant figures. Typically when you see a value like 1300 meters the zeros don’t count, but we can avoid ambiguity by using scientific notation and writing 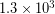 meters or using a metric prefix and writing 1.3 kilometers[4]. The table below will help you deal with zeros.
meters or using a metric prefix and writing 1.3 kilometers[4]. The table below will help you deal with zeros.
| Result | Number of Placeholder Zeros | Number of Significant Figures |
| 300.0 | 0 | 4 |
| 0.0003 | 4 | 1 |
| 0.000300 | 1 (first one) | 6 |
| 300.07 | 0 | 5 |
| 300.0700 | 0 | 7 |
| 375 | 0 | 3 |
| 3,750,000 | 3 (typically) | 3 (typically) |
| 3.75 x 103 | 0 | 3 |
Reinforcement Activity
Determine how many significant figures are in each of these reported results:
Reinforcement Activity
Use the reported uncertainties to adjust each of the following results to the correct number of significant figures:
Method of Significant Figures
Sometimes values are reported without uncertainty, but the level of uncertainty is still implied by the number of significant figures. When we express measured values, we can only list as many digits as we initially measured with our measuring tool. Tyler reported his first PD measurement as 56 mm, but he could not express this value as 56.31 mm because his measuring tool lacked the precision to measure down to the hundredth of a millimeter. Tyler had to decide which millimeter marking lined up with his pupil so the 1 mm digit has significant uncertainty. The last digit in a measured value has always been estimated in some way by the person performing the measurement. Using the method of significant figures, the last digit written down in a measurement is the first digit with some uncertainty. [5] In this way significant figures indicate the precision of a measuring tool that was used to measure a value.
Whether uncertainties are written out or implied, we still need to account for the fact that measured values have uncertainty when we use those values in calculations. We will use four general rules to determine the number significant figures in our final answers.
- 1) For multiplication and division, the final answer should have the same number of significant figures as the least number of significant figures in any of the values being multiplied or divided.
- 2) For addition and subtraction, the final answer should have the same number of decimal places as the least number of decimals in any of the values being added or subtracted.
- 3) Counting discrete objects may have zero uncertainty. For example, sitting at a table with three oranges on it, you can measure the number of oranges to be: oranges
- 4) Definitions can have zero uncertainty. For example, the definition of a kilometer is 100 meters, so if using this conversion factor in a calculation it does not contribute to adjusting your significant figures.
Each of Tyler’s PD measurements are reported to the one’s place due to his rulers’ precision. He took the average to get the final result:
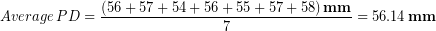
We see that to take the average Tyler had to add up the values:
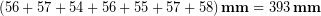
Applying the rule for addition (rule # 2), the result must have its last digit in the ones place because that was the least number of decimals in any number we used.
Tyler then divided by the number seven to get the average, but because this is just a count of how many measurements we made it has no uncertainty and doesn’t affect the significant figures. So applying the rule for division, the final result should have the same number of significant figures as the least number in the division, which in this case is the three significant figures in 393 mm. Therefore our final result would be 56.1 mm. This result has more significant figures than the result we originally determined by simply looking at the range of values to roughly estimate the uncertainty; but remember we expected that quick method to be an overestimate of uncertainty so this result makes sense.
Reinforcement Activity
Let’s return to our everyday example of Ronnie estimating how much money he will spend on gas driving back and forth from campus this term. A round-trip to campus is 14.2 miles, his car typically gets 27 miles per gallon (MPG) and gas is currently $2.86 per gallon. He needs to drive to campus and back 4 times per week. We calculated his cost for gas during the 11 week term:
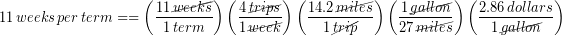
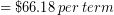
Correct the result of this calculation to have the correct number of significant figures.
- "Uncertainty in Measurement Results" by NIST Reference on Constants Units and Uncertainty, National Institute of Standards and Technology↵
- "Experimental Uncertainty" by EngineerItProgram, California State University, Chio↵
- "Uncertainty in Measurement Results" by NIST Reference on Constants Units and Uncertainty, National Institute of Standards and Technology↵
- OpenStax, College Physics. OpenStax CNX. Jul 6, 2018 http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.20. ↵
- OpenStax, College Physics. OpenStax CNX. Jul 6, 2018 [1]http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.20. ↵