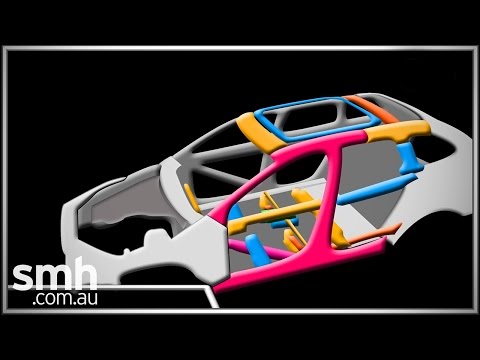
10.5: Crumple Zones
- Page ID
- 17794
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As we discussed how crumple zones reduce force on the car by extending the distance over which the car’s kinetic energy is transferred out, you might have wondered, “transferred out to where?” If so, that was very perceptive, because in fact the Principle of Conservation of Energy tells us that energy cannot be created or destroyed, only transferred from one form to another and/or one object to another, via work. The negative work done on the car by the wall during the crash in fact transferred kinetic energy into both potential energy and thermal energy or both. The video is posted again below for reference:
Thermal Energy
The force applied to the materials during the collision caused a stress on the materials. That stress caused a strain in the materials. Some materials were stressed above their ultimate strength so they fractured. Some other materials didn’t fracture, but were stressed beyond their elastic limit and into their plastic region so that they were permanently deformed. In either case, the work done to deform the materials transferred kinetic energy into thermal energy, effectively slowing the car down, but warming it up.
Reinforcement Exercises
Grab a paperclip and bend it rapidly back and forth, being sure to bend it past its elastic limit each time (far enough that it won’t spring back to its original position on its own). Now touch the crease. You might notice that the paperclip feels warm. This is because you have done work on the paperclip to cause the plastic deformation, which is a reconfiguration of molecules, and that reconfiguration gave them more microscopic kinetic energy, or thermal energy. Doing work implies a transfer of energy, where do you think the energy received by the paper clip was transferred from?
Microscopic Kinetic Energy
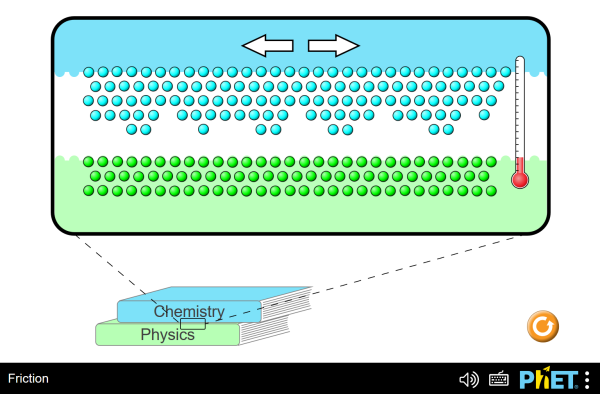
Now that we have introduced thermal energy as a new type of energy, we will reverse course and say that thermal energy is not actually a new type of energy, but rather just kinetic energy on a microscopic scale. Thermal energy is the energy stored in the motion of atoms and molecules that make up a material. Transferring thermal energy to a system really just means that you caused it’s atoms and molecules to move faster. The work done in compressing objects past their elastic limit and the work done by kinetic friction will always transfer some energy into thermal energy. You can visualize this microscopic process for kinetic friction using the simulation below.
Elastic Potential Energy
Finally, near the end of the collision the now reconfigured materials were continued to be compressed, but now the stress decreased below the yield points of the materials, so they were being compressed in theirelastic region. The work done in compressing the materials transferred kinetic energy from the car into elastic potential energy stored in the compression of the materials. This stored energy has the potential to become kinetic energy, which is exactly what happens when the materials then spring back causing the car to “bounce” back from the wall. (The objects don’t return to the fully original shape because the were permanently deformed during the first part of the crash). The car was moving forward, then for a moment it was stopped and thus had zero kinetic energy, and then it was moving backward, so once again it had kinetic energy. Some of the original kinetic energy was stored as elastic potential energy and then released as kinetic energy again. The car was not moving as fast backward after the collision as it was forward before the collision, so most of the initial kinetic energy became thermal energy and only a small part of was stored as potential energy and then released again as kinetic energy.
Reinforcement Exercise
Grab the paperclip again. Bend it just enough so that it springs back when released. You applied a force over a distance to bend the clip, therefore you did work and transferred potential energy into the paperclip. When you release the paperclip, what happens to that potential energy?
Why doesn’t the paper clip keep vibrating for ever?
Elastic Collisions
If the car had bounced back at the same speed that it had entering the collision, then the final kinetic energy would be the same as the initial, and we would say that kinetic energy had been conserved (remained constant through the collision. Such a collision is known as a perfectly elastic collision (or totally elastic collision). When a collision is not elastic, we say it is inelastic and does not conserve kinetic energy. The perfectly inelastic collisions we discussed previously are the extreme example of inelastic collisions. The relative elasticity of collisions is defined by the coefficient of restitution (COR) which relates the final kinetic energy and the initial kinetic energy. For a moving object striking a stationary object, as in the crumple zone video, the COR is calculated as final speed divided by initial speed.
(1)
![]()
A perfectly elastic collision would have a COR of one. Perfectly elastic collisions don’t really occur, but many situations come very close and we can approximate them as perfectly elastic.
Reinforcement Exercises
Try the springy paperclip experiment again. Did the paperclip continue to oscillate between being in motion and being bent so that it was transferring energy back and forth from kinetic to potential forever?
Is the bending paperclip a totally elastic process?
If not, where did the energy eventually go?
Crumple Zones
We have arrived at the most important design feature of the crumple zone. Not only does it reduce the force on the car by increasing the distance over which work is done, it also minimizes the bounce-back by ensuring that kinetic energy is not conserved. This technique requires that materials fail (crumple) so that kinetic energy is transferred into thermal energy. Imagine if this did not occur and the collision was elastic, the people inside would still be moving forward due inertia just as the dashboard came back at them, doubling the the effective impact speed.
We can view this result in the context of the impulse-momentum theorem when mass is constant:
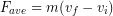
If the final velocity (and kinetic energy) is zero the impulse would be:
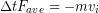
However, if the collision was elastic the final velocity is equal, but opposite, to the initial velocity:
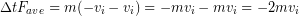
In the perfectly elastic case the impulse on the car (and the people inside) would be twice as big. This is why cars have crumple zones instead of being made out of rubber. While rubber cars might not need repairs after an accident, the occupants surely would. Repairing cars is much less expensive than attempting to repair people, and we are much better at it.
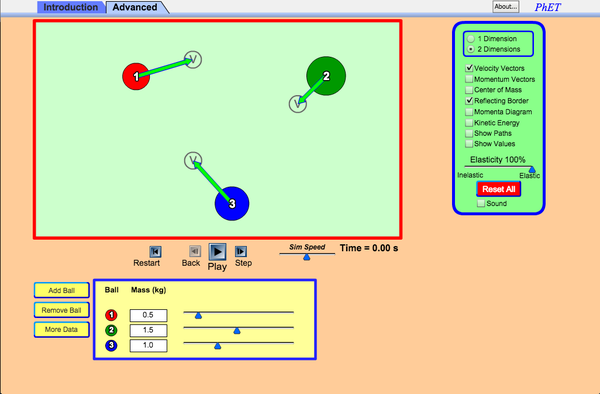
Play with this simulation of collisions, including elastic and inelastic types.